Jianfeng Xiang | Blogs | FlexGEMM：高性能稀疏卷积的跨平台后端

前言

做科研，很多时候也是一种如何最大化手中资源价值的艺术。

在开发 3D 生成模型 Trellis.2 的过程中，我逐渐感到硬件环境成为了我的限制。随着稀疏卷积分辨率的提升，显存占用和计算量也水涨船高。然而，我能用来训练的高性能 NVIDIA GPU 数量有限，而更多先进的 AMD GPU 却因兼容性问题几乎无法派上用场。当时主流的稀疏卷积库（如 spconv [1] 和 torchsparse [2]）几乎都深度依赖 CUDA 生态——在 AMD GPU 上基本无法运行。换句话说，明明算力触手可及，却被软件生态的壁垒“锁死”。对科研而言，这种局面极为令人沮丧。

也正是在这种背景下，我意识到需要 FlexGEMM ——一个既能榨干稀疏计算性能，又能在不同 GPU 平台间平稳切换的通用后端。

要真正实现这样一个跨平台后端，并非易事。起初，我尝试基于现有稀疏卷积库进行移植，但这些代码高度依赖 CUDA 内核和 PTX 汇编，几乎与 NVIDIA 生态深度绑定，迁移到 AMD 平台几乎不可能。

直到我接触到 Triton [3]，才打开了一条新的道路。Triton 是 OpenAI 开发的 GPU 编程语言，它用类似 Python 的语法抽象了 GPU 内核编写，让我能够在更高层次上直接控制计算并行模式和内存访问。更关键的是，Triton 的后端不仅支持 CUDA，还逐步在 ROCm（AMD GPU 的软件栈）上建立了完善支持。这意味着，我终于可以用同一套代码驱动不同平台的 GPU。

在科研实践中，这一点至关重要：我不再需要为硬件差异维护两套实现，也无需担心某部分算力被长期闲置。Triton 提供的统一编程范式，正是构建 FlexGEMM 的基石。

此外，Triton 还内置了许多针对不同硬件架构的优化策略，例如共享内存的高效使用、全局内存的向量化对齐访问、矩阵乘法的硬件加速，以及通过流水线隐藏缓存延迟。这些技术原本需要大量特定平台和硬件型号的经验（比如 Tensor Core 的使用），学习成本高、代码难以通用。而通过 Triton，内核开发者只需编写一份代码，编译器就能在不同平台上发挥出接近最佳的性能。这样，用 Triton 实现的内核不仅可以在现有硬件上加速，还能“战未来”，无需大量新代码就能适配新硬件。

得益于 Triton 的跨平台能力与灵活优化，FlexGEMM 在实际 3D 稀疏卷积任务中表现非常出色：相比现有主流库，在 FP16/TF32 等高效数值格式下，它能带来高达约 2× 的加速。不仅如此，它还能在 NVIDIA 和 AMD GPU 上无缝运行，无需维护多套代码。换句话说，FlexGEMM 不仅让算力充分释放，更为科研工作提供了真正的灵活性和可扩展性——无论是现有硬件还是未来的新 GPU，都能轻松驾驭。

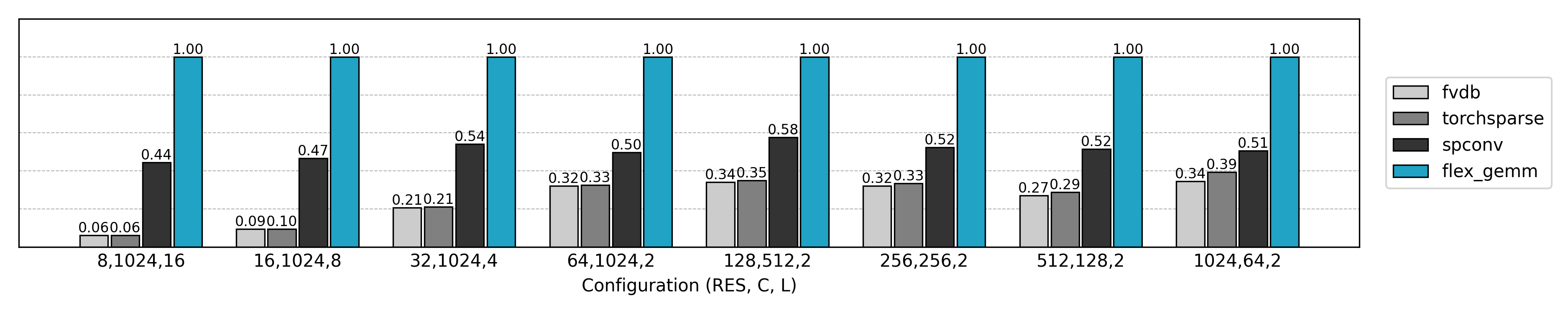
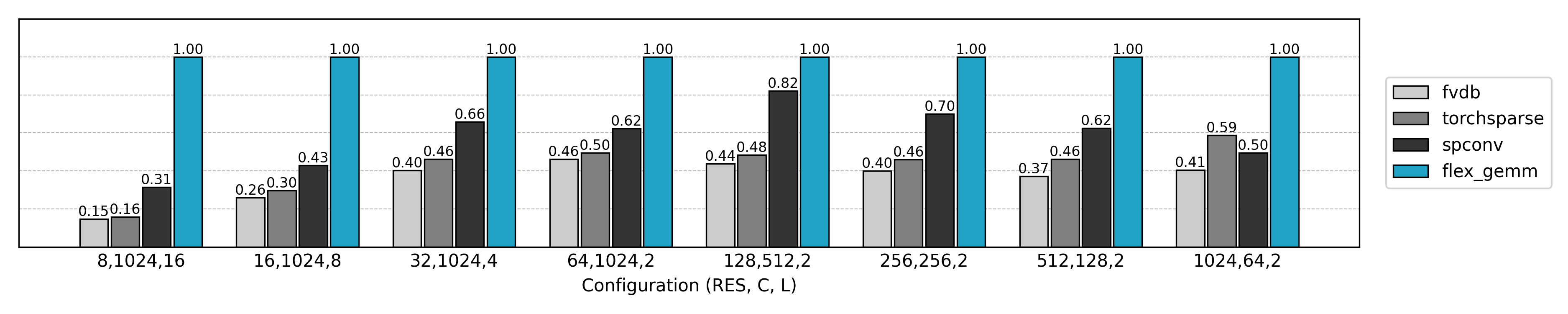
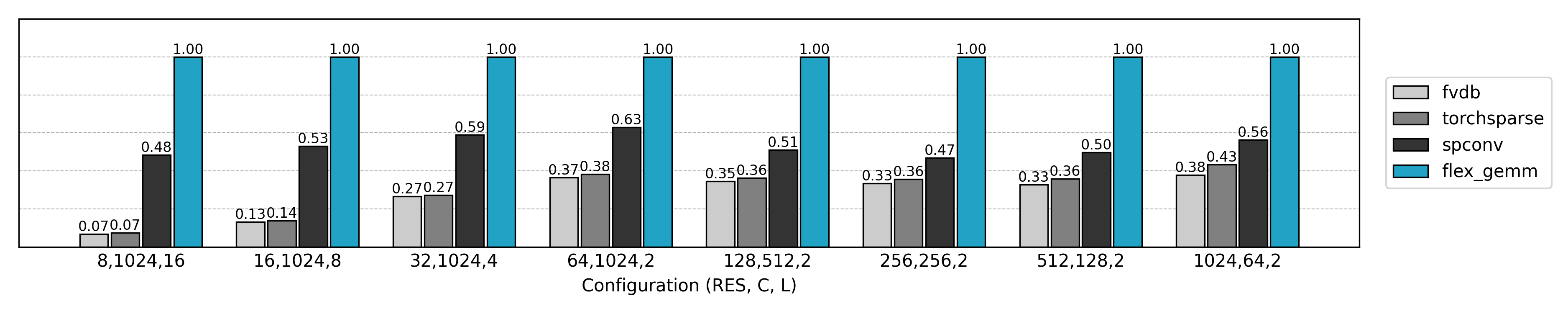
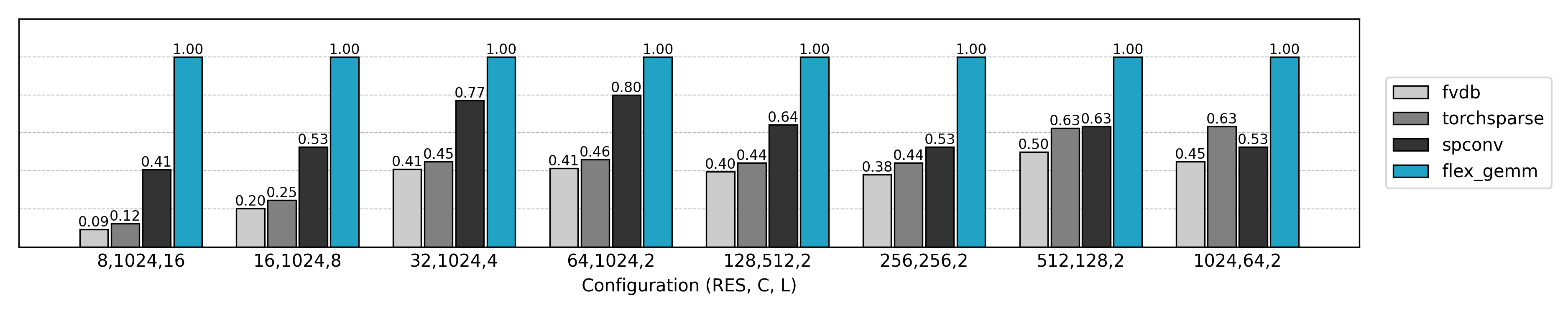
从 Naive 卷积开始

在深入 FlexGEMM 的实现之前，我们先从最直观的稀疏卷积实现方式讲起。熟悉经典卷积的读者可能已经知道，卷积运算可以被等价地转化为矩阵乘法：其中第一个操作数是经过 im2col 展开的特征图（将局部邻域铺平成列），第二个操作数则是卷积核权重。换句话说，卷积本质上就是一次大规模的 GEMM（通用矩阵乘法）：

import torch
import torch.nn.functional as F

# 参数定义
B, Ci, Co, K, H, W = 1, 3, 4, 3, 5, 5   # batch, in_channels, out_channels, kernel, height, width

# 输入: [B, Ci, H, W]
x = torch.randn(B, Ci, H, W)

# 卷积核: [Co, Ci, K, K]
weight = torch.randn(Co, Ci, K, K)

# 使用 im2col 展开输入邻域
# unfold 输出: [B, Ci*K*K, L], 其中 L = H*W (加 padding 后的位置数)
cols = F.unfold(x, kernel_size=K, padding=K//2)   # [B, Ci*K*K, H*W]

# 转置得到 [B, L, Ci*K*K]
cols = cols.transpose(1, 2)   # [B, H*W, Ci*K*K]

# 展开权重: [Co, Ci*K*K]
w = weight.view(Co, -1)       # [Co, Ci*K*K]

# GEMM: [B, L, Ci*K*K] @ [Ci*K*K, Co] = [B, L, Co]
out = cols @ w.T              # [B, H*W, Co]

# 恢复为 feature map: [B, Co, H, W]
out = out.transpose(1, 2).view(B, Co, H, W)

这种算法被称为 Explicit GEMM，即显式通用矩阵乘法。通过显式地构造出展平后的输入特征图，卷积可以使用一个矩阵乘法来完成。

对于稀疏卷积，我们也可以借鉴这一流程，先实现一个朴素的算法。然而，这里的主要难点在于如何高效获取稀疏输入特征图的局部邻域。与稠密张量不同，稀疏张量的邻居坐标无法通过简单的张量切片或代数索引直接获得，而需要依赖额外的数据结构与搜索过程。

获取局部邻域

获取稀疏数据局部邻域的算法和数据结构有很多种，已有方法中，O-CNN [4] 借助八叉树进行空间加速，fVDB [5] 则利用 VDB 数据结构实现高效索引。而在 FlexGEMM 中，我选择了最为直接的一种方式：基于哈希表的邻域查询。

GPU 上的哈希表

这里我参考了 Nosferalatu 的极简 CUDA 哈希表实现 [6]，它采用开放寻址和线性探测的策略，并利用原子操作来保证并发安全。相比于需要锁机制的复杂数据结构，这种方法更契合 GPU 的高并行性。下面给出插入和查找的核心实现：

__forceinline__ __device__ void linear_probing_insert(
    uint32_t* hashmap,
    const uint32_t keys,
    const uint32_t values,
    const int64_t N
) {
    uint32_t slot = hash(keys, N);
    while (true) {
        uint32_t prev = atomicCAS(&hashmap[slot], K_EMPTY, keys);
        if (prev == K_EMPTY || prev == keys) {
            hashmap[slot + N] = values;
            return;
        }
        slot = (slot + 1) % N;
    }
}

__forceinline__ __device__ uint32_t linear_probing_lookup(
    const uint32_t* hashmap,
    const uint32_t keys,
    const int64_t N
) {
    uint32_t slot = hash(keys, N);
    while (true) {
        uint32_t prev = hashmap[slot];
        if (prev == K_EMPTY) {
            return K_EMPTY;
        }
        if (prev == keys) {
            return hashmap[slot + N];
        }
        slot = (slot + 1) % N;
    }
}

这里的 hashmap 实际上由两部分组成：前半部分存储 keys，后半部分存储对应的 values。因此数组大小为 2N。

hashmap[slot] 存放 key
hashmap[slot + N] 存放 value

插入（insert）

首先通过 hash(keys, N) 计算初始槽位。
使用 atomicCAS（原子比较交换）尝试写入 key：
- 若槽位为空（K_EMPTY），则直接写入 key 并存储 value。
- 若槽位已有相同的 key，则更新 value。
- 否则发生冲突，通过线性探测 (slot + 1) % N 继续寻找空槽位。

查找（lookup）

同样先哈希定位。
若当前位置为空，说明 key 不存在；
若命中相同 key，则返回对应 value；
若 key 不匹配，则继续线性探测，直到找到目标或遇到空槽。

这种方式简单且高效，尤其适合 GPU 环境下的大规模并行查询。虽然在最坏情况下线性探测会导致较长的查找链，但在合理的负载因子下，它依然能保持较高的吞吐率。

对于哈希函数，我沿用了参考实现中的 murmur3 哈希函数：

__forceinline__ __device__ uint32_t hash(uint32_t k, uint32_t N) {
    k ^= k >> 16;
    k *= 0x85ebca6b;
    k ^= k >> 13;
    k *= 0xc2b2ae35;
    k ^= k >> 16;
    return k % N;
}

插入稀疏张量坐标

上面的实现针对的是 uint32 标量 key。要处理稀疏张量的 三维（或四维）坐标并不复杂，只需将其序列化为一个唯一的 uint32 key 即可。下面的 CUDA kernel 演示了如何将稀疏张量坐标 [b, x, y, z] 插入哈希表：

/**
 * Insert 3D coordinates into the hashmap using index as value
 * 
 * @param N         number of elements in the hashmap
 * @param M         number of 3d coordinates
 * @param W         the number of width dimensions
 * @param H         the number of height dimensions
 * @param D         the number of depth dimensions
 * @param hashmap   [2N] uint32 tensor containing the hashmap (key-value pairs)
 * @param coords    [M, 4] int32 tensor containing the keys to be inserted
 */
__global__ void hashmap_insert_3d_idx_as_val_cuda_kernel(
    const uint32_t N,
    const uint32_t M,
    const int W,
    const int H,
    const int D,
    uint32_t* __restrict__ hashmap,
    const int32_t* __restrict__ coords
) {
    uint32_t thread_id = blockIdx.x * blockDim.x + threadIdx.x;
    if (thread_id < M) {
        int4 coord = reinterpret_cast<const int4*>(coords)[thread_id];
        int b = coord.x;
        int x = coord.y;
        int y = coord.z;
        int z = coord.w;
        uint32_t key = static_cast<uint32_t>((((b * W + x) * H + y) * D + z));
        linear_probing_insert(hashmap, key, thread_id, N);
    }
}

在该 kernel 中，每个线程负责处理稀疏张量中的一个元素。为了提升内存带宽利用率，程序通过 128-bit 内存对齐读取的方式一次性取出四元坐标 [b, x, y, z]。随后，坐标会通过 key = (((b * W + x) * H + y) * D + z) 映射为一个全局唯一的整数 ID。

与此同时，哈希表中 value 存储的是 thread_id，即该点在输入坐标数组中的位置。这样在后续邻域查找时，就可以直接通过哈希表获得 稀疏张量索引，进而访问对应的特征值。

细心的读者可能已经注意到，这里的 key 被定义为 uint32 类型，因此它所能表示的最大范围是 $2^{32}-1$ 个唯一 ID。换算到稀疏张量的场景，相当于在批次大小为 4 时，最多支持 约 1024 分辨率的三维体素网格。在大多数应用场景下，这样的容量已经绰绰有余。如果确实需要更大规模的分辨率，可以将 key 类型扩展为 uint64，以支持更大的整数空间。不过需要注意的是，这样做会增加哈希计算和内存访问的开销，从而带来一定的效率损失。

查询邻域索引

在完成稀疏张量坐标的哈希表构建之后，下一步就是利用这张哈希表来快速查询卷积核邻域。具体来说，我们希望在给定一个稀疏点 [b, x, y, z] 以及卷积核大小 (Kw, Kh, Kd) 的情况下，能够在 常数时间 内判断邻域点是否存在，并得到它们在稀疏张量中的索引位置。下面的 CUDA kernel 展示了如何基于哈希表高效生成 submanifold 卷积的邻域映射表：

子流形卷积（Submanifold Convolution, submconv）是稀疏卷积的一种特殊形式。在标准稀疏卷积中，卷积核可能会在邻域中引入新的活跃点（活跃区域膨胀），而子流形卷积则要求输出的活跃点与输入保持一致，不会生成新的非零点。这使得 submconv 更适合在保持稀疏性的同时进行深层网络堆叠，这也是当前3D生成任务中最常用的卷积模式。

/**
 * Lookup sparse submanifold convolution neighbor map with hashmap
 * 
 * @param N         number of elements in the hashmap
 * @param M         number of 3d coordinates
 * @param W         the number of width dimensions
 * @param H         the number of height dimensions
 * @param D         the number of depth dimensions
 * @param V         the volume of the kernel
 * @param Kw        the number of width kernel dimensions
 * @param Kh        the number of height kernel dimensions
 * @param Kd        the number of depth kernel dimensions
 * @param Dw        the dilation of width
 * @param Dh        the dilation of height
 * @param Dd        the dilation of depth
 * @param hashmap   [2N] uint32 tensor containing the hashmap (key-value pairs)
 * @param coords    [M, 4] int32 tensor containing the keys to be looked up
 * @param neighbor [M, Kw * Kh * Kd] uint32 tensor containing the submanifold convolution neighbor map
 */
__global__ void hashmap_lookup_submanifold_conv_neighbour_map_cuda_kernel(
    const uint32_t N,
    const uint32_t M,
    const int W,
    const int H,
    const int D,
    const int V,
    const int Kw,
    const int Kh,
    const int Kd,
    const int Dw,
    const int Dh,
    const int Dd,
    const uint32_t* __restrict__  hashmap,
    const int32_t* __restrict__  coords,
    uint32_t* __restrict__ neighbor
) {
    int64_t thread_id = blockIdx.x * blockDim.x + threadIdx.x;
    int half_V = V / 2 + 1;
    uint32_t idx = thread_id / half_V;
    if (idx < M) {
        int4 coord = reinterpret_cast<const int4*>(coords)[idx];
        int b = coord.x;
        int x = coord.y - Kw / 2 * Dw;
        int y = coord.z - Kh / 2 * Dh;
        int z = coord.w - Kd / 2 * Dd;
        int KhKd = Kh * Kd;
        int v = thread_id % half_V;
        
        uint32_t value = K_EMPTY;
        if (v == half_V - 1) {
            value = idx;
        }
        else {
            int kx = x + v / KhKd * Dw;
            int ky = y + v / Kd % Kh * Dh;
            int kz = z + v % Kd * Dd;
            if (kx >= 0 && kx < W && ky >= 0 && ky < H && kz >= 0 && kz < D) {
                uint32_t key = static_cast<uint32_t>((((b * W + kx) * H + ky) * D + kz));
                value = linear_probing_lookup(hashmap, key, N);
                if (value != K_EMPTY) {;
                    neighbor[value * V + V - 1 - v] = idx;
                }
            }
        }
        neighbor[idx * V + v] = value;
    }
}

在这个 kernel 中，我们为每个稀疏点构建一个 邻域索引表（neighbor map）。该表的大小为 [M, Kw * Kh * Kd]，其中 M 是稀疏点的个数，Kw, Kh, Kd 是卷积核的大小。

1. 线程分配

每个线程对应于某个稀疏点在某个卷积核位置的查询任务。即 (idx, v)：

idx 表示第 idx 个稀疏点；
v 表示卷积核内的第 v 个偏移。

2. 计算卷积核中心偏移

通过 Kw/2, Kh/2, Kd/2 将卷积核对齐到中心，使得 v=0 对应核的左上前角，v=V/2 对应核的中心。

3. 边界检查

在将卷积核平移到输入坐标上时，必须保证落点 (kx, ky, kz) 在 [0, W) × [0, H) × [0, D) 的范围内，否则该邻居无效。

4. 哈希表查询

对合法坐标 (b, kx, ky, kz) 计算唯一的整数 key，然后调用 linear_probing_lookup(hashmap, key, N) 在哈希表中查询。

若找到结果，则得到该邻居点在稀疏坐标数组中的索引；
若不存在，则记为 K_EMPTY。

5. 更新 neighbor map

将查询结果写入 neighbor[idx * V + v]。其中卷积核的中心点（v == half_V - 1）对应自身，直接设为 idx。

此外，可以利用卷积邻域的 对称性 来进一步减少计算：如果点 i 的邻居包含点 j，那么点 j 的邻居必然也包含点 i。因此在得到 value 之后，可以直接设置

neighbor[value * V + V - 1 - v] = idx;

这样就避免了对称方向上的重复哈希查找，从而将邻域查询的哈希表访问量减少近一半，大幅提高了整体效率。

通过上述流程，我们就可以在 $O(1)$ 的均摊时间复杂度下完成稀疏点的局部邻域查询，并构建出稀疏卷积所需的邻域索引表。

稀疏卷积的 Explicit GEMM 实现

在完成稀疏张量坐标的哈希表构建之后，我们就可以高效地获取每个非零元素的局部邻域了。接下来，稀疏卷积的计算可以借助 Explicit GEMM（显式通用矩阵乘法） 实现。

与稠密卷积类似，Explicit GEMM 将每个卷积操作转化为矩阵乘法：

将每个非零元素的邻域特征按照某种顺序展开成矩阵（im2col-like 展开）；
将卷积核权重展开成另一矩阵；
通过矩阵乘法计算输出特征。

不同的是，稀疏卷积只对非零元素及其邻域执行计算，因此只需对选定的坐标执行矩阵操作，而无需处理整个稠密网格。接下来我将详细介绍核心代码实现。

稀疏张量模式说明：

特征张量 feats：

形状：[N, C]

N：非零元素数量（即稀疏张量中活跃体素的个数）

C：每个体素的通道数（特征维度）

存储方式：按非零体素顺序线性排列，每行对应一个体素的特征向量

坐标张量 coords：

形状：[N, 4]

每行存储一个非零体素的坐标：[b, x, y, z]

b：批次索引

x, y, z：三维空间坐标

与 feats 按行对应，第 i 行坐标对应第 i 行特征

卷积核 weight：

形状：[Co, Kw, Kh, Kd, Ci]

Co：输出通道数

Ci：输入通道数

Kw, Kh, Kd：卷积核在宽度、高度、深度方向的尺寸

存储方式为标准的五维张量，前向计算中会展平为 [V*Ci, Co] 用于 GEMM，其中 V = Kd*Kh*Kw

邻域缓存

将上一章中提到的插入与查询过程结合，就可以得到计算稀疏卷积所需要用到的领域的索引信息：

@staticmethod
def _compute_neighbor_cache(
    coords: torch.Tensor,
    shape: torch.Size,
    kernel_size: Tuple[int, int, int],
    dilation: Tuple[int, int, int]
) -> SubMConv3dNeighborCache:
    hashmap = torch.full((2 * int(spconv.HASHMAP_RATIO * coords.shape[0]),), 0xffffffff, dtype=torch.uint32, device=coords.device)
    neighbor_map = kernels.cuda.hashmap_build_submanifold_conv_neighbour_map_cuda(
        hashmap, coords,
        W, H, D,
        kernel_size[0], kernel_size[1], kernel_size[2],
        dilation[0], dilation[1], dilation[2],
    )
    return SubMConv3dNeighborCache(**{
        'neighbor_map': neighbor_map,
    })

计算得到的 neighbor_map 为每个活跃体素预先存储了其卷积核覆盖范围内的邻居索引。换言之，它在空间上固定一个邻域窗口（由 kernel_size 与 dilation 决定），并为每个活跃体素记录下该窗口中所有可能邻居在输入稀疏张量中的位置。如果某个邻居不存在，则填入占位标记。

借助这一邻域缓存，卷积运算时便无需再次在稀疏坐标中搜索邻居，而是能够直接通过索引查表完成特征聚合。

前向过程

@staticmethod
def _sparse_submanifold_conv_forward(
    feats: torch.Tensor,
    neighbor_cache: SubMConv3dNeighborCache,
    weight: torch.Tensor,
    bias: Optional[torch.Tensor] = None,
) -> torch.Tensor:
    N = feats.shape[0]
    Co, Kw, Kh, Kd, Ci = weight.shape
    V = Kw * Kh * Kd
    neighbor_map = neighbor_cache['neighbor_map']
    
    # im2col
    im2col = torch.zeros((N * V, Ci), device=feats.device, dtype=feats.dtype)
    mask = neighbor_map.view(-1) != 0xffffffff
    im2col[mask] = feats[neighbor_map.view(-1).long()[mask]]
    im2col = im2col.view(N, V * Ci)
    
    # addmm
    weight = weight.view(Co, V * Ci).transpose(0, 1)
    if bias is not None:
        output = torch.addmm(bias, im2col, weight)
    else:
        output = torch.mm(im2col, weight)
    
    return output

在显式 GEMM 实现中，首先利用 neighbor_map 将输入稀疏张量的非零元素邻域特征展开成类似 im2col 的矩阵表示；随后将卷积核权重展平，并与该展开矩阵执行矩阵乘法，得到对应的输出特征；若包含 bias，则可通过 torch.addmm 在同一过程中高效地加到结果上。

反向过程

@staticmethod
def _sparse_submanifold_conv_backward(
    grad_output: torch.Tensor,
    feats: torch.Tensor,
    neighbor_cache: SubMConv3dNeighborCache,
    weight: torch.Tensor,
    bias: Optional[torch.Tensor] = None,
) -> Tuple[Optional[torch.Tensor], Optional[torch.Tensor], Optional[torch.Tensor]]:
    N = feats.shape[0]
    Co, Kw, Kh, Kd, Ci = weight.shape
    V = Kw * Kh * Kd

    neighbor_map = neighbor_cache['neighbor_map']
    
    if feats.requires_grad:
        # im2col
        im2col = torch.zeros((N * V, Co), device=feats.device, dtype=feats.dtype)
        inv_neighbor_map = torch.flip(neighbor_map, [1])
        mask = inv_neighbor_map.view(-1) != 0xffffffff
        im2col[mask] = grad_output[inv_neighbor_map.view(-1).long()[mask]]
        im2col = im2col.view(N, V * Co)
        
        # addmm
        grad_input = torch.mm(im2col, weight.view(Co, V, Ci).transpose(0, 1).reshape(V * Co, Ci))
    else:
        grad_input = None
        
    if weight.requires_grad:
        # im2col
        im2col = torch.zeros((N * V, Ci), device=weight.device, dtype=weight.dtype)
        mask = neighbor_map.view(-1) != 0xffffffff
        im2col[mask] = feats[neighbor_map.view(-1).long()[mask]]
        im2col = im2col.view(N, V * Ci)
        
        # addmm
        grad_weight = torch.mm(im2col.t(), grad_output.view(N, -1)).view(V, Ci, Co).permute(2, 0, 1).contiguous().view(Co, Kd, Kh, Kw, Ci)
    else:
        grad_weight = None
        
    if bias is not None and bias.requires_grad:
        grad_bias = grad_output.sum(dim=0)
    else:
        grad_bias = None

    return grad_input, grad_weight, grad_bias

在反向传播时，同样利用 neighbor_map 来避免重复搜索邻域。其思路与前向过程相对应：

对于输入梯度的计算，先将输出梯度根据邻接关系重新排列成 im2col 形式，再与卷积核权重相乘，得到输入特征的梯度；

注意，根据卷积的反向传播公式，用于展开的索引应为前向邻域索引在各个维度上的翻转版本：也就是说，卷积核中位置 $(i,j,k)$ 的梯度需要对应到位置 $(-i,-j,-k)$。在一般卷积中，这意味着需要显式构造一份反向邻域索引；但对于卷积核尺寸为奇数的子流形卷积（submanifold conv），由于卷积核中心对称，可以直接通过 inv_neighbor_map = torch.flip(neighbor_map, [1]) 获得反向邻域映射。

对于权重梯度的计算，先用 neighbor_map 将输入特征展开为 im2col 形式，再与输出梯度相乘，得到权重更新量；

若存在 bias，则直接对输出梯度在除了通道的维度上求和即可。

性能比较

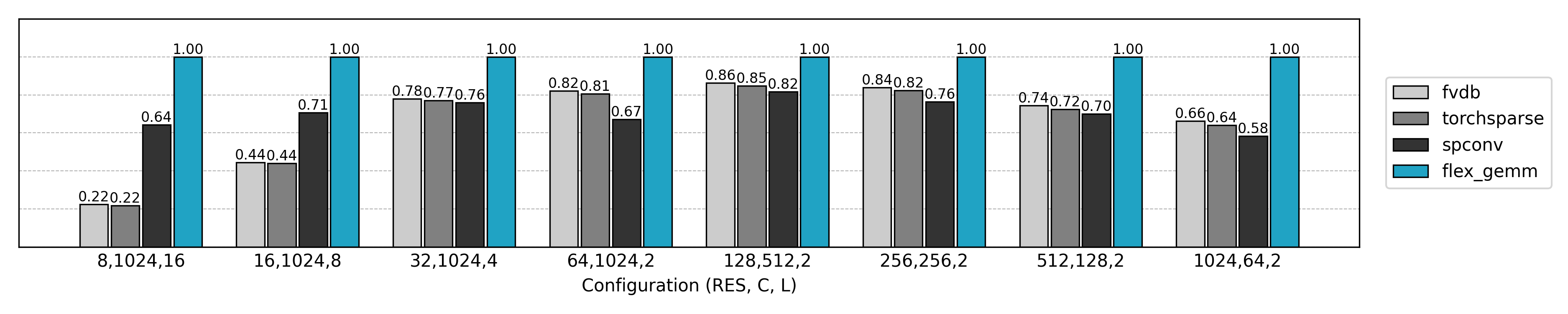
相对于最终的实现，朴素的 Explicit GEMM 实现只达到了约 10% 的性能，而却使用了 10 倍的显存。随着问题规模的扩大，Explicit GEMM 算法逐渐劣化。新的优化方法等着我们去探索。

跳过显式邻域展开：Implicit GEMM

在前面的 Explicit GEMM 中，我们利用 PyTorch 高度优化的矩阵乘法实现卷积计算，因此计算性能本身已接近最优。然而，显式构造整个局部邻域展开矩阵会带来两个问题：

首先，展开矩阵需要占用大量显存。对于输入特征 feats 形状为 [N, C]、卷积核大小为 [Kd, Kh, Kw] 的情况，展开后的矩阵大小为 [N * V, C]，其中 $V = Kd \cdot Kh \cdot Kw$。当活跃体素数量 N 较大或者卷积核尺寸较大时，显存消耗会成倍增加。

其次，更重要的是全局内存访问开销。在显式展开中，每个活跃体素的邻域特征首先需要写入一个大的展开矩阵，而在后续的矩阵乘法中，这些数据又必须重新从全局内存中读取。考虑到展开矩阵本身规模较大，这种重复访问会显著影响整体性能。

为了解决这些问题，我们可以使用 Implicit GEMM 方法：将按邻域索引读取特征和矩阵乘法计算融合到同一个 GPU kernel 中。在计算过程中，输入特征按邻域索引直接被访问，中间结果存放在共享内存中，而无需提前在全局内存中构造完整的展开矩阵。这样不仅显著降低了显存占用，也减少了大量全局内存访问，从而提升稀疏卷积在大规模数据上的计算效率。

全局内存（Global Memory）：GPU 上容量大但访问延迟高的存储，所有线程均可访问，每次读写都需要经过显存总线，适合存储输入、输出和卷积权重。

共享内存（Shared Memory）：GPU 上每个线程块内部共享的高速缓存，容量较小但访问延迟低，非常适合存放中间计算结果或小块数据，减少全局内存访问次数。

Triton 来帮忙

对于这样一个融合算子，我选用 Triton 来实现。

Triton 的核心设计目标，就是让开发者用类似 Python 的语法来编写高效 GPU kernel，同时自动获得底层 CUDA 编程里才有的优化能力。和 CUDA C++ 相比，它有以下几个突出的编码特性：

基于 Python 语法 Triton kernel 使用 Python 编写，并通过 @triton.jit 装饰器进行 JIT 编译。相比 CUDA 的 C++ 语法，Triton 更加简洁直观，尤其适合科研和快速迭代。
程序 = 一个线程块（program = block） Triton 把每个 kernel 实例称为 program，它大致对应 CUDA 中的一个线程块。你只需要思考每个 program 处理的数据块（tile）如何布局，而不必显式管理线程的 ID 和调度。
块状内存访问（Block-level Memory Access） Triton 倡导以矩形 tile 为基本单位进行加载和计算，通过 tl.load / tl.store 显式控制全局内存访问模式，天然支持向量化访问。
自动寄存器与共享内存管理 在 CUDA 里，开发者需要显式声明和管理共享内存。而在 Triton 中，编译器会根据你的 tile 大小和访问模式自动将数据放入寄存器或共享内存，从而达到类似手工优化的效果。
循环展开与流水线（Pipelining） Triton 编译器可以分析程序的访存和计算模式，自动对循环进行展开并组织流水线，在隐藏访存延迟的同时最大化算力利用率。
自动调优（Auto-tuning） Triton 提供了 @triton.autotune 装饰器，允许你为 kernel 定义多个候选配置（如 tile 大小、线程数量、流水线深度等）。在运行时，Triton 会自动 benchmark 并选择最快的配置。

比如在 Implicit GEMM 中，每个活跃体素的邻域特征都需要从全局内存中按索引加载，如果采取“先全部加载，再统一计算”的方式，GPU 在等待数据时往往会出现算力闲置。Triton 的编译器会自动进行优化：

当一个 tile 的邻域特征正在从全局内存中读取时，GPU 线程可以利用上一个 tile 已经在寄存器或共享内存中的数据继续进行矩阵运算，避免等待。
同时，Triton 会尽量生成 coalesced 访存 指令，将邻域 gather 过程组织成批量的连续内存访问，减少带宽浪费。
对于这些中间特征块，编译器会自动决定是缓存在 寄存器 还是 共享内存 中，以实现最快的重复访问。
最终，通过 @triton.autotune，不同卷积核大小或输入规模下的 tile 配置也会自动调优，从而保证这种加载–计算重叠在各种场景下都能保持高效。

读者若想要学习 Triton kernel 的基本实现方法，可以访问其官方文档中的例程：Tutorials — Triton documentation

前向过程

@triton.jit
def sparse_submanifold_conv_fwd_implicit_gemm_kernel(
    input,
    weight,
    bias,
    neighbor,
    output,
    # Tensor dimensions
    N, Ci, Co, V: tl.constexpr,
    # Meta-parameters
    B1: tl.constexpr,   # Block size for N dimension
    B2: tl.constexpr,   # Block size for Co dimension
    BK: tl.constexpr,   # Block size for K dimension (V * Ci)
    allow_tf32: tl.constexpr,  # Allow TF32 precision for matmuls
):
    """
    Sparse submanifold convolution forward kernel using implicit GEMM.
    
    Args:
        input (pointer): A pointer to the input tensor of shape (N, Ci)
        weight (pointer): A pointer to the weight tensor of shape (Co, V, Ci)
        bias (pointer): A pointer to the bias tensor of shape (Co)
        neighbor (pointer): A pointer to the neighbor tensor of shape (N, V)
        output (pointer): A pointer to the output tensor of shape (N, Co)
    """
    block_id = tl.program_id(axis=0)
    block_dim_co = tl.cdiv(Co, B2)
    block_id_co = block_id % block_dim_co
    block_id_n = block_id // block_dim_co
    
    # Create pointers for submatrices of A and B.
    num_k = tl.cdiv(Ci, BK)  # Number of blocks in K dimension
    offset_n = (block_id_n * B1 + tl.arange(0, B1)) % N         # (B1,)
    offset_co = (block_id_co * B2 + tl.arange(0, B2)) % Co      # (B2,)
    offset_k = tl.arange(0, BK)                                 # (BK,)
    
    # Create a block of the output matrix C.
    accumulator = tl.zeros((B1, B2), dtype=tl.float32)
    
    # Calculate pointers to weight matrix.
    weight_ptr = weight + (offset_co[None, :] * V * Ci + offset_k[:, None])     # (BK, B2)
    
    # Iterate along V*Ci dimension.
    for k in range(num_k * V):
        v = k // num_k
        bk = k % num_k
        # Calculate pointers to input matrix.
        neighbor_offset_n = tl.load(neighbor + offset_n * V + v)                                # (B1,)
        input_ptr = input + bk * BK + (neighbor_offset_n[:, None] * Ci + offset_k[None, :])     # (B1, BK)
        # Load the next block of input and weight.
        neigh_mask = neighbor_offset_n != 0xffffffff
        k_mask = offset_k < Ci - bk * BK
        input_block = tl.load(input_ptr, mask=neigh_mask[:, None] & k_mask[None, :], other=0.0)
        weight_block = tl.load(weight_ptr, mask=k_mask[:, None], other=0.0)
        # Accumulate along the K dimension.
        accumulator = tl.dot(input_block, weight_block, accumulator,
                             input_precision='tf32' if allow_tf32 else 'ieee')                  # (B1, B2)
        # Advance the pointers to the next Ci block.
        weight_ptr += min(BK, Ci - bk * BK)
    c = accumulator.to(input.type.element_ty)
            
    # add bias
    if bias is not None:
        bias_block = tl.load(bias + offset_co)
        c += bias_block[None, :]
                
    # Write back the block of the output matrix with masks.
    out_offset_n = block_id_n * B1 + tl.arange(0, B1)
    out_offset_co = block_id_co * B2 + tl.arange(0, B2)
    out_ptr = output + (out_offset_n[:, None] * Co + out_offset_co[None, :])
    out_mask = (out_offset_n[:, None] < N) & (out_offset_co[None, :] < Co)
    tl.store(out_ptr, c, mask=out_mask)

接下来，我们逐步拆解这段 Triton kernel，看看它是如何实现 稀疏子流形卷积（Sparse Submanifold Convolution） 的前向过程的。

1. Kernel 的总体结构

@triton.jit
def sparse_submanifold_conv_fwd_implicit_gemm_kernel(
    input,
    weight,
    bias,
    neighbor,
    output,
    # Tensor dimensions
    N, Ci, Co, V: tl.constexpr,
    # Meta-parameters
    B1: tl.constexpr,   # Block size for N dimension
    B2: tl.constexpr,   # Block size for Co dimension
    BK: tl.constexpr,   # Block size for K dimension (V * Ci)
    allow_tf32: tl.constexpr,  # Allow TF32 precision for matmuls
):

这里定义了一个 Triton kernel。

input, weight, bias, neighbor, output 都是指向 GPU 全局内存的指针。
N, Ci, Co, V 分别是输入点数、输入通道数、输出通道数、邻域大小。
B1, B2, BK 是 tile 的划分大小，也就是 kernel 的并行计算单元。
allow_tf32 用来控制是否使用 TensorFloat32 加速点积。

可以看到，这里采用了典型的 GEMM 分块计算模式：把结果矩阵 [N, Co] 切成小块，然后每个 Triton program 负责计算一个小块。

2. 程序 ID 与 tile 划分

    block_id = tl.program_id(axis=0)
    block_dim_co = tl.cdiv(Co, B2)
    block_id_co = block_id % block_dim_co
    block_id_n = block_id // block_dim_co

Triton 把每个 program（也就是一个线程块）看作处理一个输出 tile。

block_id_n 表示当前 tile 在 N 维度上的位置。
block_id_co 表示当前 tile 在 Co 维度上的位置。
所以，一个 tile 的输出范围就是 [B1 × B2]。

3. tile 的坐标范围

    offset_n = (block_id_n * B1 + tl.arange(0, B1)) % N
    offset_co = (block_id_co * B2 + tl.arange(0, B2)) % Co
    offset_k = tl.arange(0, BK)

offset_n：这一块 tile 对应的 N 索引。
offset_co：这一块 tile 对应的输出通道范围。
offset_k：对应 Ci 的分块范围，用于循环遍历输入通道。

这样，每个 tile 知道自己负责计算哪一片区域。

BK 是程序每次在矩阵乘法计算中需要求和的维度上加载的块的尺寸，因为共享内存大小的限制，我们没法一次性加载整个 [B1, Ci] 和 [Ci, B2] 的子矩阵，因此会分成多个子块加载，相乘结果循环累加到累积器上。

4. 累加器初始化

    accumulator = tl.zeros((B1, B2), dtype=tl.float32)

每个 tile 都会维护一个 B1 × B2 的累加矩阵，初始为 0。在后续循环中，输入和权重按块相乘，结果不断累加到这个 accumulator 里。

5. 主循环：按邻域和通道分块

    for k in range(num_k * V):
        v = k // num_k
        bk = k % num_k

这里的循环本质上在遍历 所有邻域位置 (V) 和 输入通道块 (Ci // BK)。也就是说，输出结果是逐个邻域、逐个通道分块地累积计算出来的。

6. 输入特征加载（隐式展开）

        neighbor_offset_n = tl.load(neighbor + offset_n * V + v)   # (B1,)
        input_ptr = input + bk * BK + (neighbor_offset_n[:, None] * Ci + offset_k[None, :])
        ...
        input_block = tl.load(input_ptr, mask=neigh_mask[:, None] & k_mask[None, :], other=0.0)

这里是整个 kernel 的核心：

neighbor 保存了稀疏点的邻居索引。
对于每个点 offset_n，取出其在第 v 个邻居上的索引。
通过 neighbor_offset_n，直接从 input 里 gather 对应特征。
注意这里用了 mask，当邻居不存在（值为 0xffffffff）时，会加载 0。

这一步其实就是 “隐式展开”：我们并没有在全局内存中显式构造 [N*V, Ci] 矩阵，而是按需、按块去加载输入。

7. 权重加载与点积

        weight_block = tl.load(weight_ptr, mask=k_mask[:, None], other=0.0)
        accumulator = tl.dot(input_block, weight_block, accumulator,
                             input_precision='tf32' if allow_tf32 else 'ieee')

weight_block：加载对应的权重块 (BK × B2)。
tl.dot：执行块矩阵乘法，并把结果累加到 accumulator。
累积时使用 FP32 精度，避免数值误差。

这就是 Implicit GEMM 的核心计算部分。

8. 写回结果

    c = accumulator.to(input.type.element_ty)
    if bias is not None:
        bias_block = tl.load(bias + offset_co)
        c += bias_block[None, :]
    out_ptr = output + (out_offset_n[:, None] * Co + out_offset_co[None, :])
    tl.store(out_ptr, c, mask=out_mask)

把 FP32 累加结果转换成和输入一致的 dtype（比如 FP16）。
如果有 bias，则逐通道加上。
通过 mask 控制边界，避免越界写入。

最终，每个 tile 的计算结果被写回全局内存，完成整个卷积的前向传播。

反向过程

反向过程分为计算对输入稀疏张量的梯度和对权重的梯度。基本实现框架和前向过程一致，这里简要列出实现的关键代码：

对输入稀疏张量的梯度

在 Explicit GEMM 实现中已经分析过，对于子流形卷积，只需要翻转邻域索引后执行输出梯度和卷积核的卷积即可：

neighbor_offset_n = tl.load(neighbor + offset_n * V + V - 1 - v)

对卷积权重的梯度

将输出梯度与按邻域索引展开后的输入做矩阵乘法：

mask = offset_k < N - k * BK
# Calculate pointers to input matrix.
input_offset_n = tl.load(neighbor_ptr, mask=mask[:, None], other=0xffffffff)            # (BK, BV)
input_ptr = input + (input_offset_n[:, :, None] * Ci + offset_ci[None, None, :])        # (BK, BV, BCi)
# Load the next block of input and weight.
grad_output_block = tl.load(grad_output_ptr, mask=mask[None, :], other=0.0)
input_block = tl.load(input_ptr, mask=input_offset_n[:, :, None] != 0xffffffff, other=0.0).reshape(BK, BV * BCi)
# Accumulate along the K dimension.
accumulator = tl.dot(grad_output_block, input_block, accumulator,
                    input_precision='tf32' if allow_tf32 else 'ieee')                  # (B1, B2)

性能比较

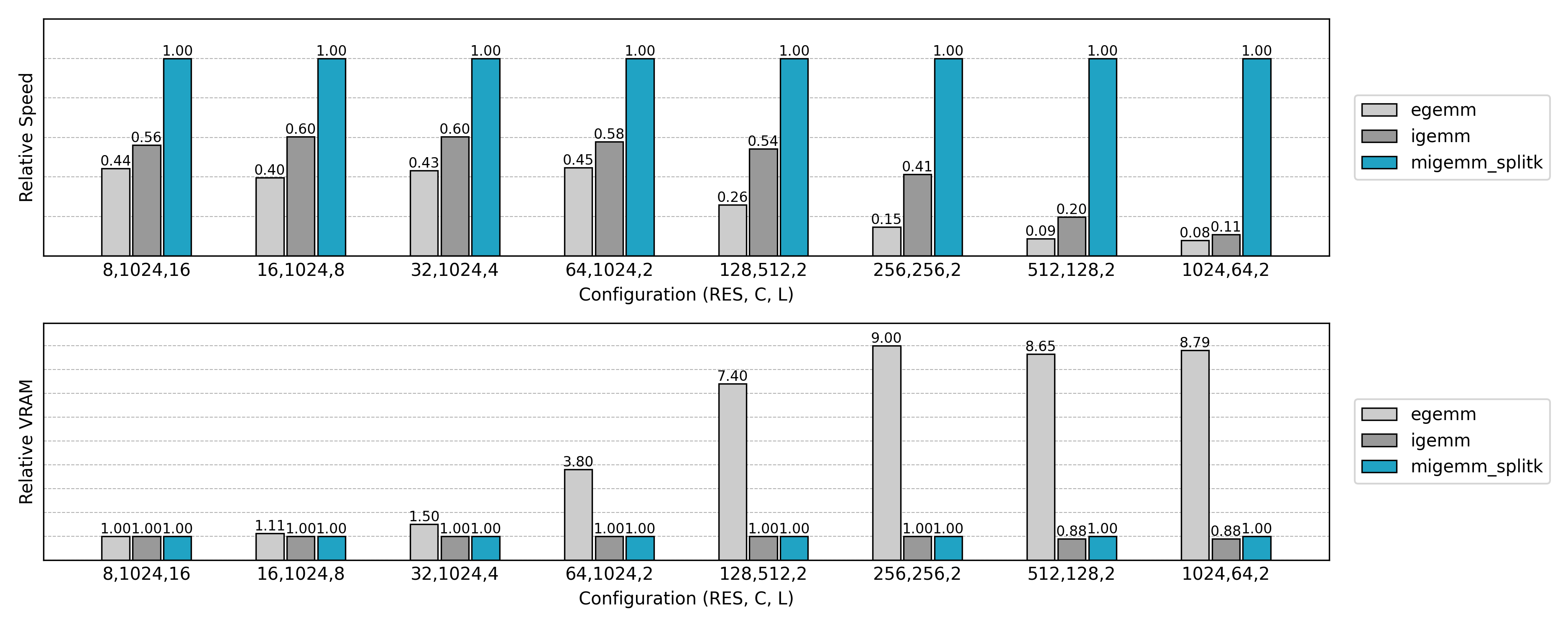
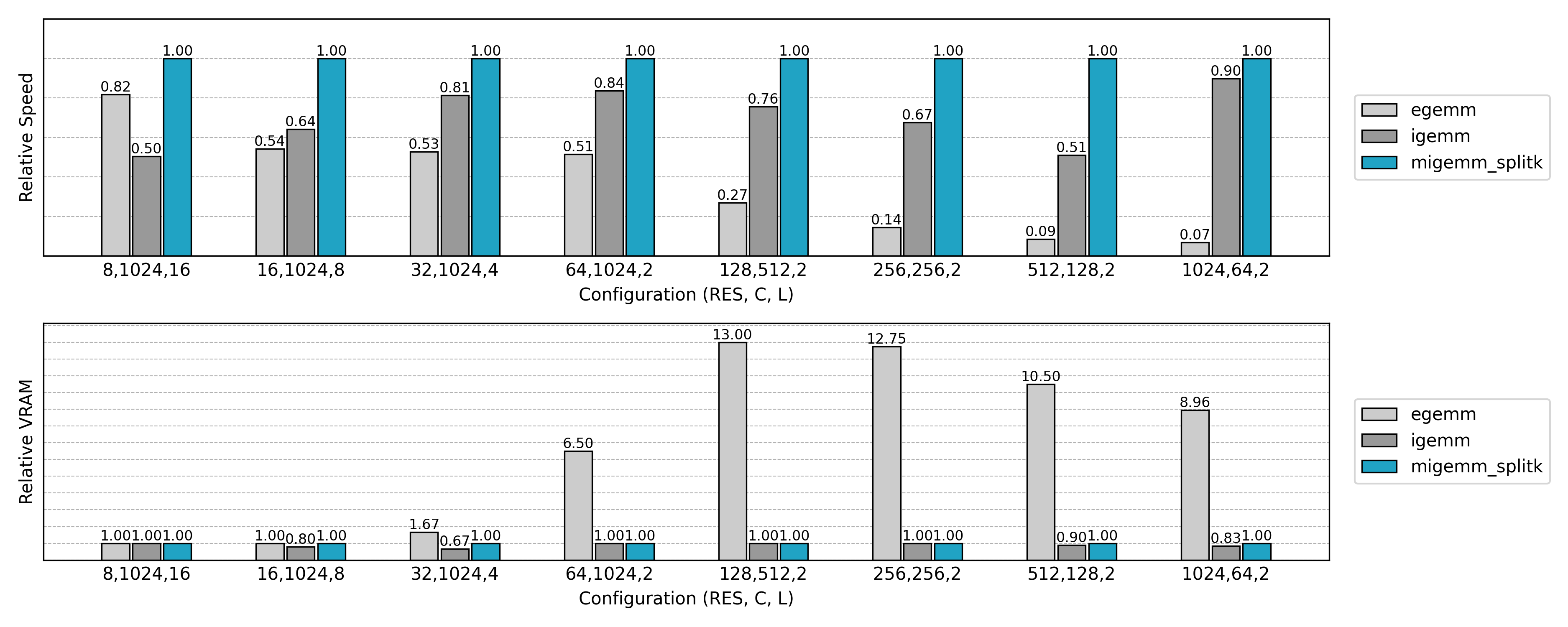
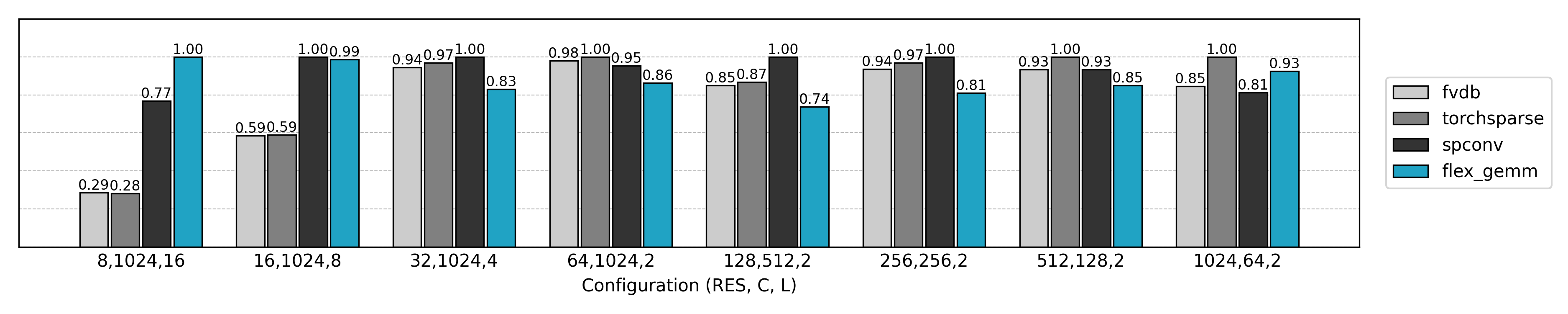
与先前实现的 Explicit GEMM 算法比较，可见非常可观的性能提升和显存消耗的降低。但是也有一些反常的结果：小空间尺寸、大通道数量时推理速度不如朴素方法，大空间尺寸、小通道数量时训练速度几乎无提升。这些现象值得进一步分析。

提升并行度：Split K

观察前面的速度测试，我们可以发现一些情况下的运行速度与最终实现相差较大：

小空间尺寸、大通道数量时：前向过程和对输入稀疏张量的反向过程
大空间尺寸、小通道数量时：对卷积权重的反向过程

这两种情况有一个共同的性质：GEMM 的 K 维度（即累加维度）较大，而 M 或 N 维度（即并行度来源）不足。

以前向过程为例，整体计算量由三个维度的乘积构成：

M 维：对应输入体素数 N
N 维：对应输出通道数 Co
K 维：对应邻域大小与输入通道数 V * Ci

如果 M 或 N 较小，而 K 很大，就会出现问题：GPU 上并行发生在 tile 层次上，但 M、N 太小的情况下，计算任务只能划分成较少的 tile （依照前文实现，为 ((M + B1 - 1) // B1) * ((N + B2 -1) // B2)）。而 K 维虽然很大，但它是“串行累加”的维度，不能天然提供并行。结果就是 GPU 上线程数不够，SM 计算单元出现空闲，性能大幅下降。

在更细粒度上并行

为了解决这个问题，可以引入 Split K 技术：

将原本在 K 维上的累加任务拆分成多个子任务，每个子任务负责一部分 K 范围的计算。
每个子任务可以作为一个独立的 kernel program 并行运行，从而增加整体并行度。
所有子任务完成后，再在 M、N 维度上把结果做一次归约（reduce），得到最终的输出。

公式化来看：

\[\boldsymbol{C} = \boldsymbol{A} \times \boldsymbol{B} \quad (\boldsymbol{A}\in\mathbb{R}^{M \times K}, \boldsymbol{B}\in\mathbb{R}^{K \times N})\]

如果把 K 划分为 S 段：

\[C = \sum_{s=0}^{S-1} A_{[:, K_s]} \times B_{[K_s, :]}\]

其中每个 $A_{[:, K_s]} \times B_{[K_s, :]}$ 就可以并行计算。

当然，Split K 并不是免费的：

需要额外一次 归约（reduce），把多个子任务的部分和累积到一起。
这会带来一些全局内存写回和读写的开销。
但在并行度严重不足的情况下，这部分代价远小于 GPU 空闲带来的浪费。

因此，Split K 一般只在 M 或 N 过小的情况下启用。实际实现中，可以通过 autotune 自动选择是否启用，以及选择合适的 S 值。

代码实现

以子流形卷积的前向过程为例，反向过程类似修改即可：

@triton.jit
def sparse_submanifold_conv_fwd_implicit_gemm_splitk_kernel(
    input,
    weight,
    bias,
    neighbor,
    output,
    # Tensor dimensions
    N, Ci, Co, V: tl.constexpr,
    # Meta-parameters
    B1: tl.constexpr,   # Block size for N dimension
    B2: tl.constexpr,   # Block size for Co dimension
    BK: tl.constexpr,   # Block size for K dimension (V * Ci)
    SPLITK: tl.constexpr,  # Split K dimension
    allow_tf32: tl.constexpr,  # Allow TF32 precision for matmuls
):
    """
    Sparse submanifold convolution forward kernel using implicit GEMM with split K dimension.
    
    Args:
        input (pointer): A pointer to the input tensor of shape (N, Ci)
        weight (pointer): A pointer to the weight tensor of shape (Co, V, Ci)
        bias (pointer): A pointer to the bias tensor of shape (Co)
        neighbor (pointer): A pointer to the neighbor tensor of shape (N, V)
        output (pointer): A pointer to the output tensor of shape (N, Co)
    """
    block_id_k = tl.program_id(axis=1)  # SplitK dimension
    block_id = tl.program_id(axis=0)
    block_dim_co = tl.cdiv(Co, B2)
    block_id_co = block_id % block_dim_co
    block_id_n = block_id // block_dim_co
    
    # Create pointers for submatrices of A and B.
    num_k = tl.cdiv(Ci, BK)  # Number of blocks in K dimension
    k_start = tl.cdiv(num_k * V * block_id_k, SPLITK)
    k_end = tl.cdiv(num_k * V * (block_id_k + 1), SPLITK)
    offset_n = (block_id_n * B1 + tl.arange(0, B1)) % N         # (B1,)
    offset_co = (block_id_co * B2 + tl.arange(0, B2)) % Co      # (B2,)
    offset_k = tl.arange(0, BK)                                 # (BK,)
    
    # Create a block of the output matrix C.
    accumulator = tl.zeros((B1, B2), dtype=tl.float32)
    
    # Calculate pointers to weight matrix.
    weight_ptr = weight + k_start * BK + (offset_co[None, :] * V * Ci + offset_k[:, None])     # (BK, B2)
    
    # Iterate along V*Ci dimension.
    for k in range(k_start, k_end):
        v = k // num_k
        bk = k % num_k
        # Calculate pointers to input matrix.
        neighbor_offset_n = tl.load(neighbor + offset_n * V + v)                                # (B1,)
        input_ptr = input + bk * BK + (neighbor_offset_n[:, None] * Ci + offset_k[None, :])     # (B1, BK)
        # Load the next block of input and weight.
        neigh_mask = neighbor_offset_n != 0xffffffff
        k_mask = offset_k < Ci - bk * BK
        input_block = tl.load(input_ptr, mask=neigh_mask[:, None] & k_mask[None, :], other=0.0)
        weight_block = tl.load(weight_ptr, mask=k_mask[:, None], other=0.0)
        # Accumulate along the K dimension.
        accumulator = tl.dot(input_block, weight_block, accumulator,
                             input_precision='tf32' if allow_tf32 else 'ieee')                  # (B1, B2)
        # Advance the pointers to the next Ci block.
        weight_ptr += min(BK, Ci - bk * BK)
            
    # add bias
    if bias is not None and block_id_k == 0:
        bias_block = tl.load(bias + offset_co)
        accumulator += bias_block[None, :]
                
    # Write back the block of the output matrix with masks.
    out_offset_n = block_id_n * B1 + tl.arange(0, B1)
    out_offset_co = block_id_co * B2 + tl.arange(0, B2)
    out_ptr = output + block_id_k * N * Co + (out_offset_n[:, None] * Co + out_offset_co[None, :])
    out_mask = (out_offset_n[:, None] < N) & (out_offset_co[None, :] < Co)
    tl.store(out_ptr, accumulator, mask=out_mask)

上面的 kernel 与之前的 Implicit GEMM 实现整体框架相似，但核心变化在于 如何处理 K 维度。我们逐步对比这两份代码，看看 SplitK 带来了哪些不同。

1. 多了一维 program_id

block_id_k = tl.program_id(axis=1)  # SplitK dimension
block_id = tl.program_id(axis=0)

在普通的 Implicit GEMM 中，每个 program 只通过 axis=0 来区分 (N, Co) tile。而在 SplitK 中，我们额外引入了 axis=1，表示在 K 维度上的拆分段编号。这样，每个 (N, Co) tile 可以被多个 program 并行计算，每个 program 只处理 K 维的一部分。

2. 确定 K 范围

num_k = tl.cdiv(Ci, BK)
k_start = tl.cdiv(num_k * V * block_id_k, SPLITK)
k_end = tl.cdiv(num_k * V * (block_id_k + 1), SPLITK)

普通 Implicit GEMM 会完整遍历 K = V * Ci，而 SplitK 将其划分为 SPLITK 段：

k_start、k_end 表示当前 block_id_k 负责的 K 范围；
这样即使 N 或 Co 较小，也能通过拆分 K 来增加并行度。

3. 循环范围缩小

for k in range(k_start, k_end):
    ...

相比 Implicit GEMM 遍历所有 num_k * V，这里的循环仅覆盖 [k_start, k_end)，对应权重指针从 k_start 开始。这正是 SplitK 的关键：每个 program 只计算一部分 K 的贡献。

4. Bias 处理逻辑改变

if bias is not None and block_id_k == 0:
    bias_block = tl.load(bias + offset_co)
    accumulator += bias_block[None, :]

在 Implicit GEMM 中，每个 (N, Co) tile 都会直接加一次 bias。而在 SplitK 中，同一个 (N, Co) tile 可能被多个 program 计算，如果 bias 在每个分段都加一次，结果就会重复。因此这里加了限制：只在 block_id_k == 0 时加 bias。

5. 输出写回到分段缓冲区

out_ptr = output + block_id_k * N * Co + (out_offset_n[:, None] * Co + out_offset_co[None, :])

在 Implicit GEMM 中，结果直接写回到 [N, Co]。在 SplitK 中，每个 block_id_k 会把结果写到独立的缓冲区段（第 block_id_k 份）。最终的输出张量形状相当于 [SPLITK, N, Co]，需要在 kernel 外做一次规约（reduce sum），才能得到真正的 [N, Co]。

性能比较

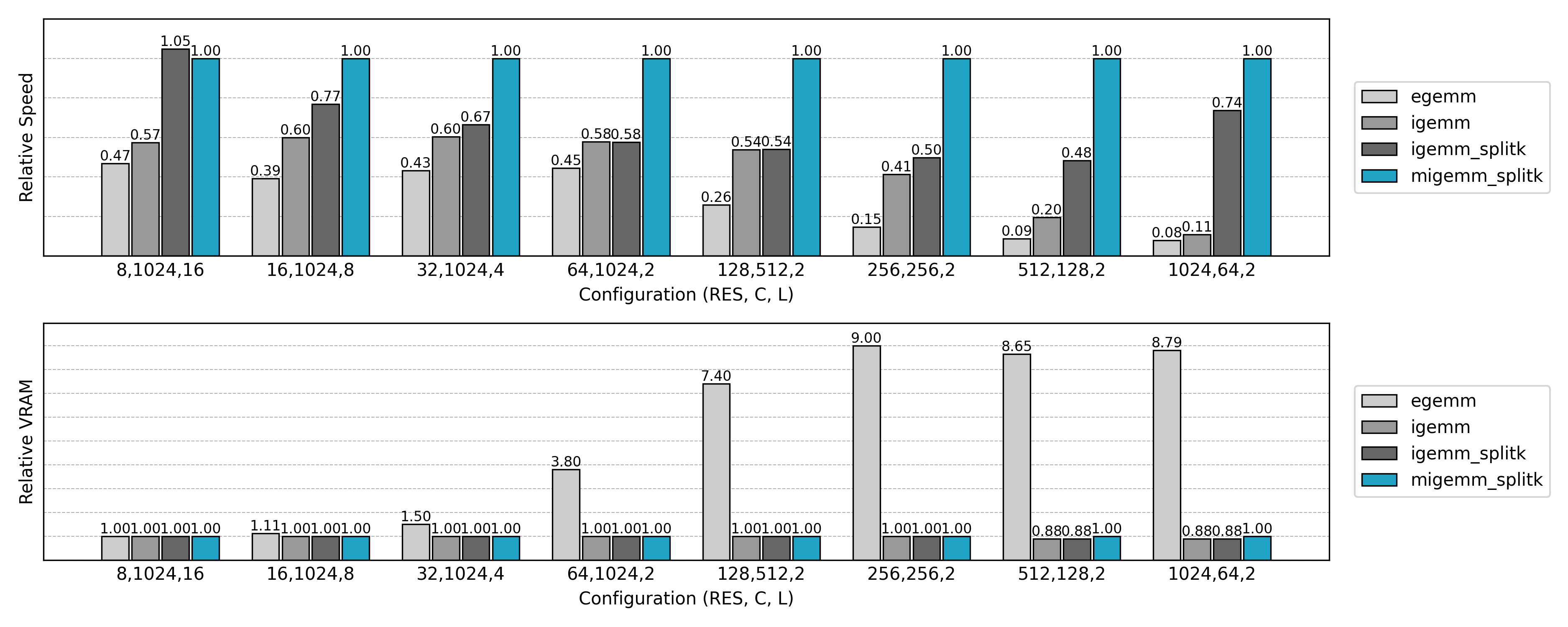
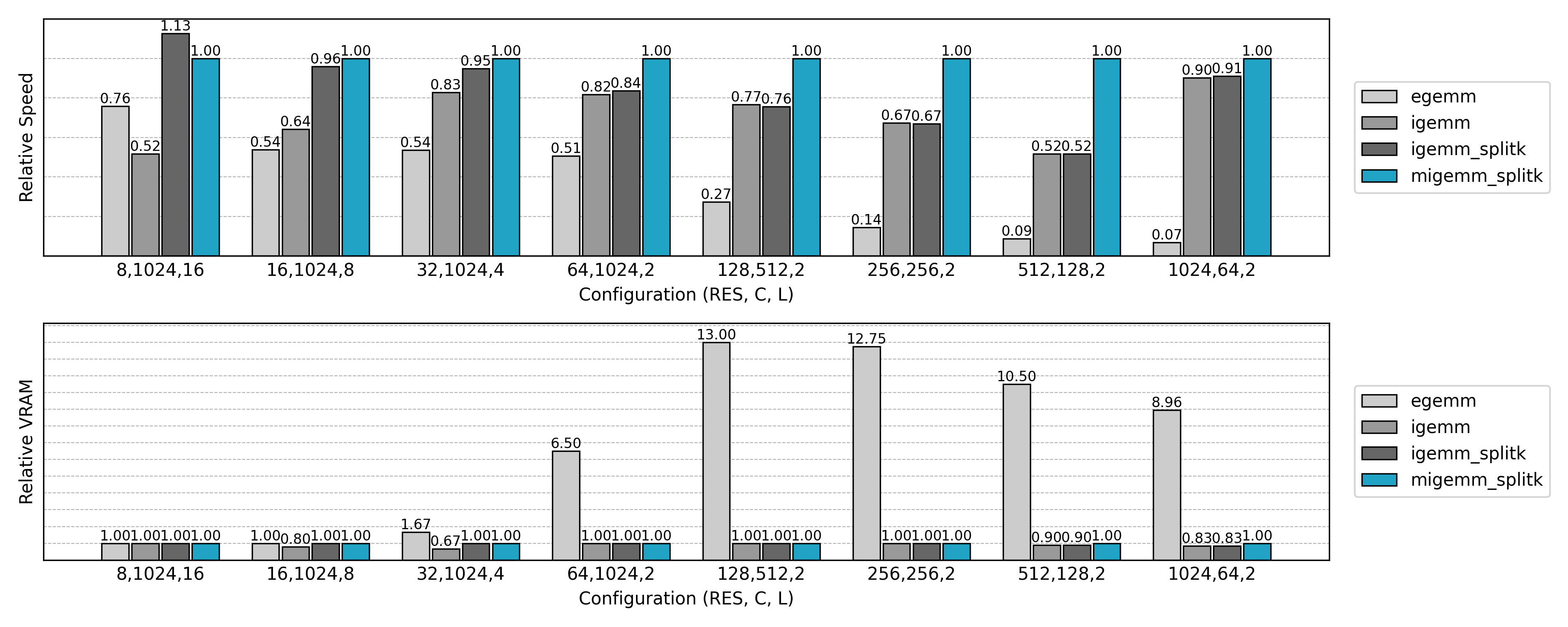
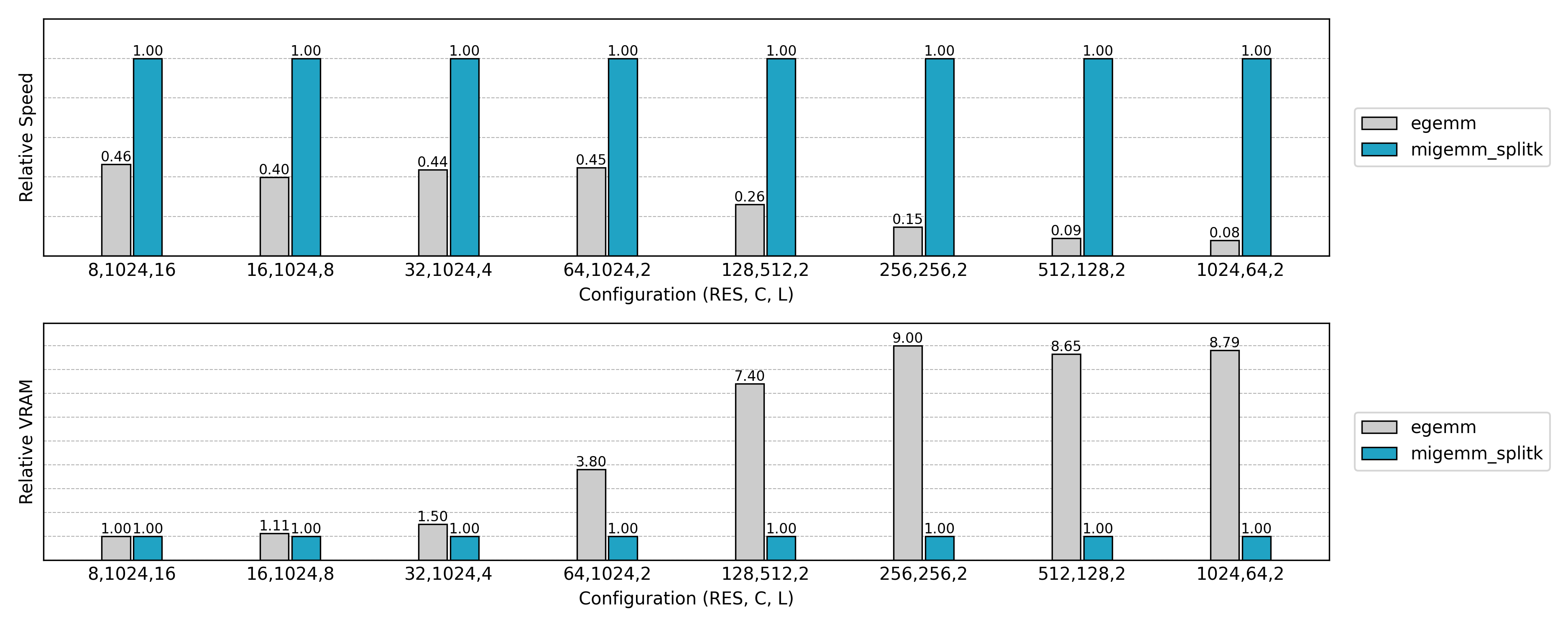
与先前实现的非 Split K 版本比较，可见小 N 或小 Co 场景下的 GPU 利用率显著提升。

减少对空邻域的计算：Masked Implicit GEMM

在稀疏卷积中，很多活跃体素的某些邻域位置实际上是“空”的（即没有有效邻居，代码中用 0xffffffff 表示）。如果仍按照完整的 V 遍历所有邻域位置，我们会在这些“空”上做大量无用的加载与乘加，浪费内存带宽与算力。这就引出了下一步优化的目标——跳过（或最小化）这些空邻域的计算，把计算资源集中在真实存在的邻居上，从而在高度稀疏的场景下获得明显加速。

在 CPU 上实现这一优化很简单：遍历邻居时，遇到无效索引直接 continue。

但在 GPU 上，由于 单指令多数据（SIMD） 的执行模型，每个 warp 内的线程必须保持一致的执行路径。只有所有进程中的某个邻居都为空时，我们才能跳过这一邻居对应的访存和计算，实现加速。如果不同线程在某些邻居位置上「分支不同」（一些有邻居，一些没有），则 GPU 会按照有邻居的情况执行，不会得到加速。

单指令多数据（SIMD）
在 GPU 上，一个 warp（通常 32 个线程）只能同时执行同一条指令，只是操作的数据不同。
如果 warp 内的线程遇到分支条件（有的执行 if 分支，有的执行 else 分支），GPU 会把这两个分支顺序执行，再把结果合并，这就是所谓的 warp divergence（分支发散）。
因此，在高效的 GPU kernel 中，需要尽量保证同一线程块中的所有线程执行相同的命令来最大化效率

更好的任务分配

在这种情况下，一个关键问题就出现了：如何把邻居 mask 更合理地分配到计算 block 中？

设想我们有很多个活跃体素，每个体素的邻居 mask 是一个二进制向量（1 表示该邻居存在，0 表示空）。如果把这些 mask 随意分配到 block 里，就可能出现某个 block 内的邻居模式差异巨大：

有的线程在某个邻居位置上为 1，需要做访存和乘加；
有的线程在同一个邻居位置上为 0，其实不需要算。

结果就是整个 warp 依然得执行这一步计算，空邻居线程也被迫「陪跑」，导致效率下降。

换句话说，每个 block 内的所有线程邻居 mask 的并集决定了这个 block 必须执行多少邻居位置。于是我们的优化目标可以抽象成：

将所有邻居 mask 分组，每组大小固定（对应 block 大小），最小化所有组内的 mask 的并集的大小之和。

从算法角度看，这是一个难以求解的划分问题，但我们可以借助一些启发式方法来逼近最优。

格雷码排序

在实际实现中，一个非常简单但有效的方法是 格雷码排序（Gray Code Ordering）。

格雷码有一个重要性质：相邻编码之间只相差一位。这意味着如果我们按照格雷码顺序对体素的邻居 mask 进行重新排列，相邻元素的二进制模式会尽量相似。

于是我们可以利用这一点：

首先把所有体素的邻居 mask 映射到格雷码序；
按照格雷码顺序排列这些体素；
再按照固定的 block 大小依次切分。

这样得到的分组有一个自然的好处：每个 block 内的 mask 在比特空间上“邻近”，它们的差异集中在少量比特位上。这样一来，同一个 block 内的线程间执行逻辑的不一致性更低，浪费的计算更少，从而减少 GPU 需要执行的邻居访存与乘加操作。

邻域缓存信息

后续 Masked Implicit GEMM kernel 将依赖以下缓存信息：

neighbor_map：与 Explicit/Implicit GEMM 相同，用于记录体素与其邻域索引的映射关系，空位置以 0xffffffff 标记；
sorted_idx：在格雷码顺序重新排序后，得到的活跃体素索引序列；
valid_kernel_{block_size} 与 valid_kernel_seg_{block_size}：在指定 block 大小下，每个 block 对应的有效邻居集合。该索引会排除所有进程均为空的邻居位置，因此表现为一个变长数组列表，供后续 kernel 高效索引；
valid_signal_i / valid_signal_o 与 valid_signal_seg：记录每个邻居位置对应的有效输入张量与输出张量索引对，用于卷积权重的梯度反向传播。

总体而言，这些缓存信息可以理解为 在算子执行前构建的执行计划。借助这些计划，Masked Implicit GEMM kernel 在运行时既能保持 SIMD 友好性，又能最大限度地跳过空邻域计算，从而在高度稀疏的输入上实现显著加速。

这部分的 CUDA 实现相对简单，读者可参考 flex_gemm\kernels\cuda\spconv\neighbor_map.cu (L255) 获取具体代码，并结合 flex_gemm\ops\spconv\submanifold_conv3d.py (L9) 了解 Python 侧的接口。

前向过程

利用重新组织的计算计划和保存的邻域缓存信息，这里展示子流形卷积前向过程的 Masked Implicit GEMM 算法的 triton 实现：

@triton.jit
def sparse_submanifold_conv_fwd_masked_implicit_gemm_splitk_kernel(
    input,
    weight,
    bias,
    neighbor,
    sorted_idx,
    output,
    # Tensor dimensions
    N, Ci, Co, V: tl.constexpr,
    # Meta-parameters
    B1: tl.constexpr,   # Block size for N dimension
    B2: tl.constexpr,   # Block size for Co dimension
    BK: tl.constexpr,   # Block size for K dimension (V * Ci)
    SPLITK: tl.constexpr,  # Split K dimension into multiple sub-dimensions
    allow_tf32: tl.constexpr,  # Allow TF32 precision for matmuls
    # Huristic parameters
    valid_kernel,
    valid_kernel_seg,
):
    """
    Sparse submanifold convolution forward kernel using masked implicit GEMM split-k.
    
    Args:
        input (pointer): A pointer to the input tensor of shape (N, Ci)
        weight (pointer): A pointer to the weight tensor of shape (Co, V, Ci)
        bias (pointer): A pointer to the bias tensor of shape (Co)
        neighbor (pointer): A pointer to the neighbor tensor of shape (N, V)
        sorted_idx (pointer): A pointer to the sorted index tensor of shape (N)
        valid_kernel (pointer): A pointer to the valid neighbor index tensor of shape (L)
        valid_kernel_seg (pointer): A pointer to the valid neighbor index segment tensor of shape (BLOCK_N + 1)
        output (pointer): A pointer to the output tensor of shape (N, Co)
    """
    block_id_k = tl.program_id(axis=1)  # SplitK dimension
    block_id = tl.program_id(axis=0)
    block_dim_co = tl.cdiv(Co, B2)
    block_id_co = block_id % block_dim_co
    block_id_n = block_id // block_dim_co
    
    # Create pointers for submatrices of A and B.
    num_k = tl.cdiv(Ci, BK)  # Number of blocks in K dimension
    valid_kernel_start = tl.load(valid_kernel_seg + block_id_n)
    valid_kernel_seglen = tl.load(valid_kernel_seg + block_id_n + 1) - valid_kernel_start
    k_start = tl.cdiv(num_k * valid_kernel_seglen * block_id_k, SPLITK)
    k_end = tl.cdiv(num_k * valid_kernel_seglen * (block_id_k + 1), SPLITK)
    offset_n = block_id_n * B1 + tl.arange(0, B1)
    n_mask = offset_n < N
    offset_sorted_n = tl.load(sorted_idx + offset_n, mask=n_mask, other=0)  # (B1,)
    offset_co = (block_id_co * B2 + tl.arange(0, B2)) % Co                  # (B2,)
    offset_k = tl.arange(0, BK)                                             # (BK,)
    
    # Create a block of the output matrix C.
    accumulator = tl.zeros((B1, B2), dtype=tl.float32)
    
    # Iterate along V*Ci dimension.
    for k in range(k_start, k_end):
        v = k // num_k
        bk = k % num_k
        v = tl.load(valid_kernel + valid_kernel_start + v)
        # Calculate pointers to input matrix.
        neighbor_offset_n = tl.load(neighbor + offset_sorted_n * V + v)                             # (B1,)
        input_ptr = input + bk * BK + (neighbor_offset_n[:, None] * Ci + offset_k[None, :])         # (B1, BK)
        # Calculate pointers to weight matrix.
        weight_ptr = weight + v * Ci + bk * BK + (offset_co[None, :] * V * Ci + offset_k[:, None])  # (BK, B2)
        # Load the next block of input and weight.
        neigh_mask = neighbor_offset_n != 0xffffffff
        k_mask = offset_k < Ci - bk * BK
        input_block = tl.load(input_ptr, mask=neigh_mask[:, None] & k_mask[None, :], other=0.0)
        weight_block = tl.load(weight_ptr, mask=k_mask[:, None], other=0.0)
        # Accumulate along the K dimension.
        accumulator = tl.dot(input_block, weight_block, accumulator,
                             input_precision='tf32' if allow_tf32 else 'ieee')                      # (B1, B2)
            
    # add bias
    if bias is not None and block_id_k == 0:
        bias_block = tl.load(bias + offset_co)
        accumulator += bias_block[None, :]
                
    # Write back the block of the output matrix with masks.
    out_offset_n = offset_sorted_n
    out_offset_co = block_id_co * B2 + tl.arange(0, B2)
    out_ptr = output + block_id_k * N * Co + (out_offset_n[:, None] * Co + out_offset_co[None, :])
    out_mask = n_mask[:, None] & (out_offset_co[None, :] < Co)
    tl.store(out_ptr, accumulator, mask=out_mask)

下面我们逐段来看优化后 Masked Implicit GEMM 配合 Split K 的实现：

1. Block ID 与维度划分

block_id_k = tl.program_id(axis=1)  # SplitK dimension
block_id = tl.program_id(axis=0)
block_dim_co = tl.cdiv(Co, B2)
block_id_co = block_id % block_dim_co
block_id_n = block_id // block_dim_co

这里与普通 SplitK 版本类似：

block_id_n 控制输入点的分块
block_id_co 控制输出通道的分块
block_id_k 控制 K 维的拆分

2. 有效邻域范围

valid_kernel_start = tl.load(valid_kernel_seg + block_id_n)
valid_kernel_seglen = tl.load(valid_kernel_seg + block_id_n + 1) - valid_kernel_start
k_start = tl.cdiv(num_k * valid_kernel_seglen * block_id_k, SPLITK)
k_end = tl.cdiv(num_k * valid_kernel_seglen * (block_id_k + 1), SPLITK)

这里是 Masked 算法的关键区别：

每个输入点 block_id_n 对应的有效 kernel 范围，通过 valid_kernel_seg 分段获取；
遍历范围 k_start ~ k_end 不再是全量的 V * Ci，而是 只覆盖有效的卷积核位置。

相比普通版本，这里减少了大量空迭代。

3. 邻域点索引 & 输入块加载

v = tl.load(valid_kernel + valid_kernel_start + v)
neighbor_offset_n = tl.load(neighbor + offset_sorted_n * V + v)    # (B1,)
input_ptr = input + bk * BK + (neighbor_offset_n[:, None] * Ci + offset_k[None, :])

这里的 v 来自 valid_kernel（有效卷积核索引），而不是原始 0 ~ V-1 的全范围。并且对 input 的访问按格雷码顺序重排，来减少无效邻居并缩小访存和计算冗余。

另外 neigh_mask = neighbor_offset_n != 0xffffffff 用来屏蔽无效点。

4. 权重块加载 & 乘法累积

weight_ptr = weight + v * Ci + bk * BK + (offset_co[None, :] * V * Ci + offset_k[:, None])
input_block = tl.load(input_ptr, mask=neigh_mask[:, None] & k_mask[None, :], other=0.0)
weight_block = tl.load(weight_ptr, mask=k_mask[:, None], other=0.0)
accumulator = tl.dot(input_block, weight_block, accumulator,
                     input_precision='tf32' if allow_tf32 else 'ieee')

这里与普通 SplitK 类似：

tl.dot 进行矩阵乘累积
利用 mask 保证越界位置不被访问

不同点在于：

权重只针对 valid_kernel 的位置取值，而非全量 V。

5. 写回结果

out_offset_n = offset_sorted_n
out_offset_co = block_id_co * B2 + tl.arange(0, B2)
out_ptr = output + block_id_k * N * Co + (out_offset_n[:, None] * Co + out_offset_co[None, :])
tl.store(out_ptr, accumulator, mask=out_mask)

写回过程与普通 SplitK 相同。如果 SPLITK > 1，后续会在归约 kernel 中对同一输出块的不同 block_id_k 结果做额外求和。

反向过程

Masked Implicit GEMM 的前向过程通过 有效邻域索引 跳过了空邻域，减少了无用计算，反向过程的设计逻辑类似。这里简要的介绍下实现的要点，具体代码读者可移步代码仓库查看。

对输入特征的梯度： 只需将权重翻转后再做一次与输出梯度的卷积即可，代码中只需反向加载权重：
```
weight_ptr = weight + (((offset_k[:, None] + bk * BK) * V + V - 1 - v) * Ci + offset_ci[None, :])
```
对卷积权重的梯度： 使用缓存阶段保存的 valid_signal_i/o 加载输入特征和输出梯度，进行矩阵乘法的累积即可，必要时做 Split K 优化。

性能比较

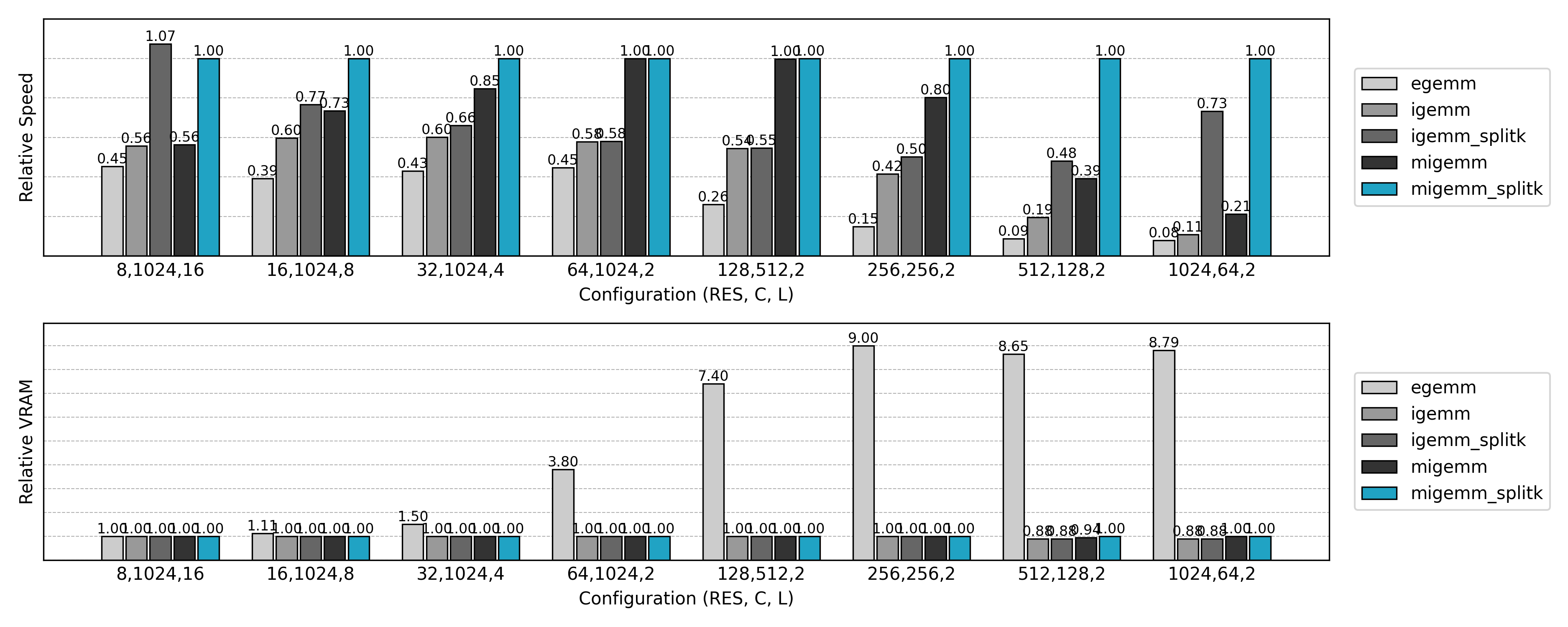
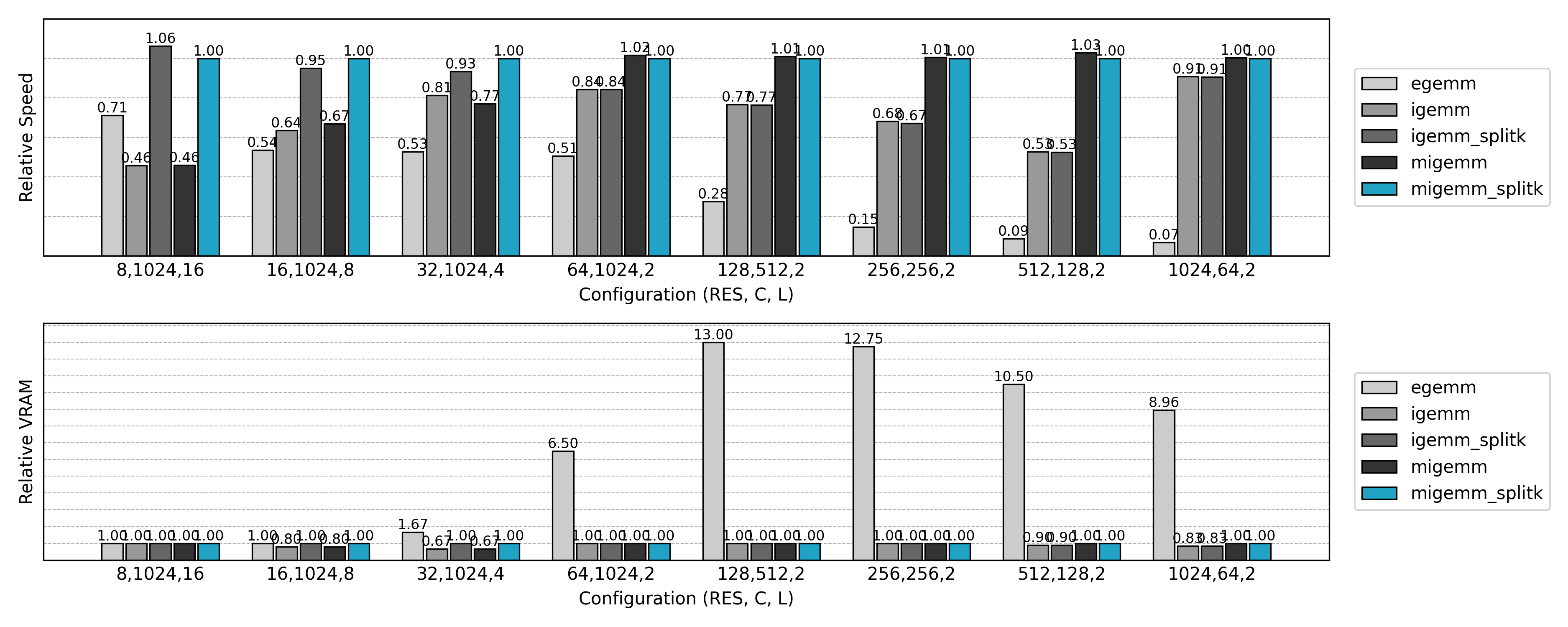
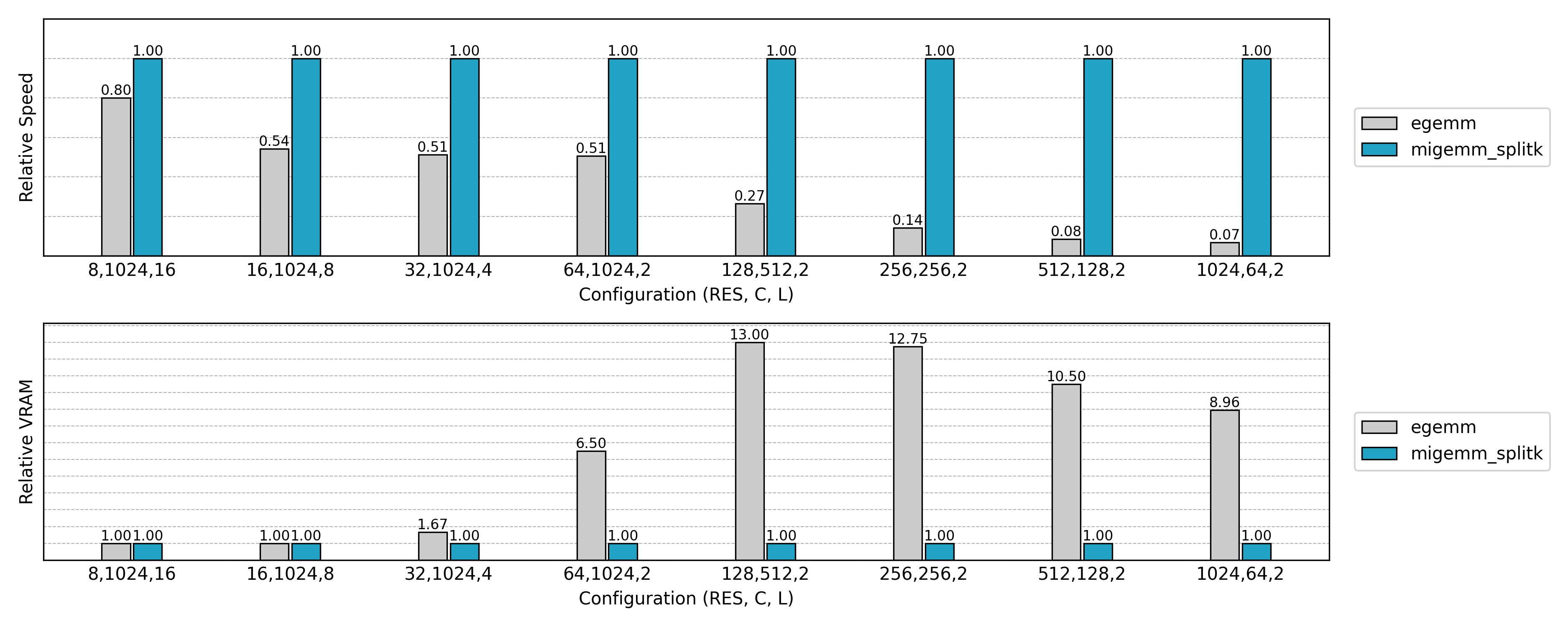
从速度测试结果可知，Masked Implicit GEMM 往往能比普通 Implicit GEMM 再提升 20%~40% 的速度。

总结

FlexGEMM 中稀疏卷积的高效实现，经历了一段持续演进的过程。

作为一切的基石，哈希表被用来实现邻域查询，从而在稀疏场景下快速建立卷积所需的邻接关系。

最初的思路是将卷积运算转化为标准的矩阵乘法。Explicit GEMM 通过类似 im2col 的展开方式，最大化利用了现有高性能矩阵库的计算能力，但由于大量的全局内存使用，其效率和其显存开销均不够理想。

为缓解这一问题，Implicit GEMM 被提出：避免显式展开，直接在核函数中按需计算，减少了内存占用。然而，它在并行调度上仍存在 warp divergence 的冗余，因线程间的邻居访问模式不一致而浪费了计算能力。

为进一步提升算力利用率，Masked Implicit GEMM 在此基础上引入了掩码机制，通过跳过无效计算和优化线程调度，取得了更理想的性能。

与之正交的另一项改进 SplitK 将矩阵乘法中的累加维度再拆分为许多子任务，最后再进行规约，极大提升了特定情况下算法的并行度和执行效率。

这条演进路径清晰地展示了稀疏卷积从“可行”到“高效”的逐步过渡：每一代方法都在解决前一代的不足。最终，Masked Implicit GEMM 与 SplitK 的结合通常能带来最佳性能。但与此同时，早期的 Explicit 与 Implicit 实现依然保留了重要价值——它们完整呈现了思路演进的脉络，也为后续研究与优化提供了参考。

在我们的 3D 生成模型 Trellis。2 中，FlexGEMM 已经成为核心算子之一。它让我们能够在有限的硬件环境下，仍然支撑起更高分辨率的实验，并保证推理过程的高效稳定。

FlexGEMM 已经完全开源，期待社区在实际使用中进一步拓展这些思路，推动稀疏卷积算子的持续优化。