代码重构
为了方便后续的代码编写与维护,我们采用面向对象的思想,将不同的图形抽象成类,而所有的图形共有一父类——Figure。这个父类规定了子类,即不同图形,需完成的接口(这里就是符号距离函数),也储存子类所共有的属性,如颜色、模糊、透明度等。而各个特定图形子类拥有各自的属性来决定其形状,并完成父类遗留的符号距离函数接口。
下面是上述结构的UML图
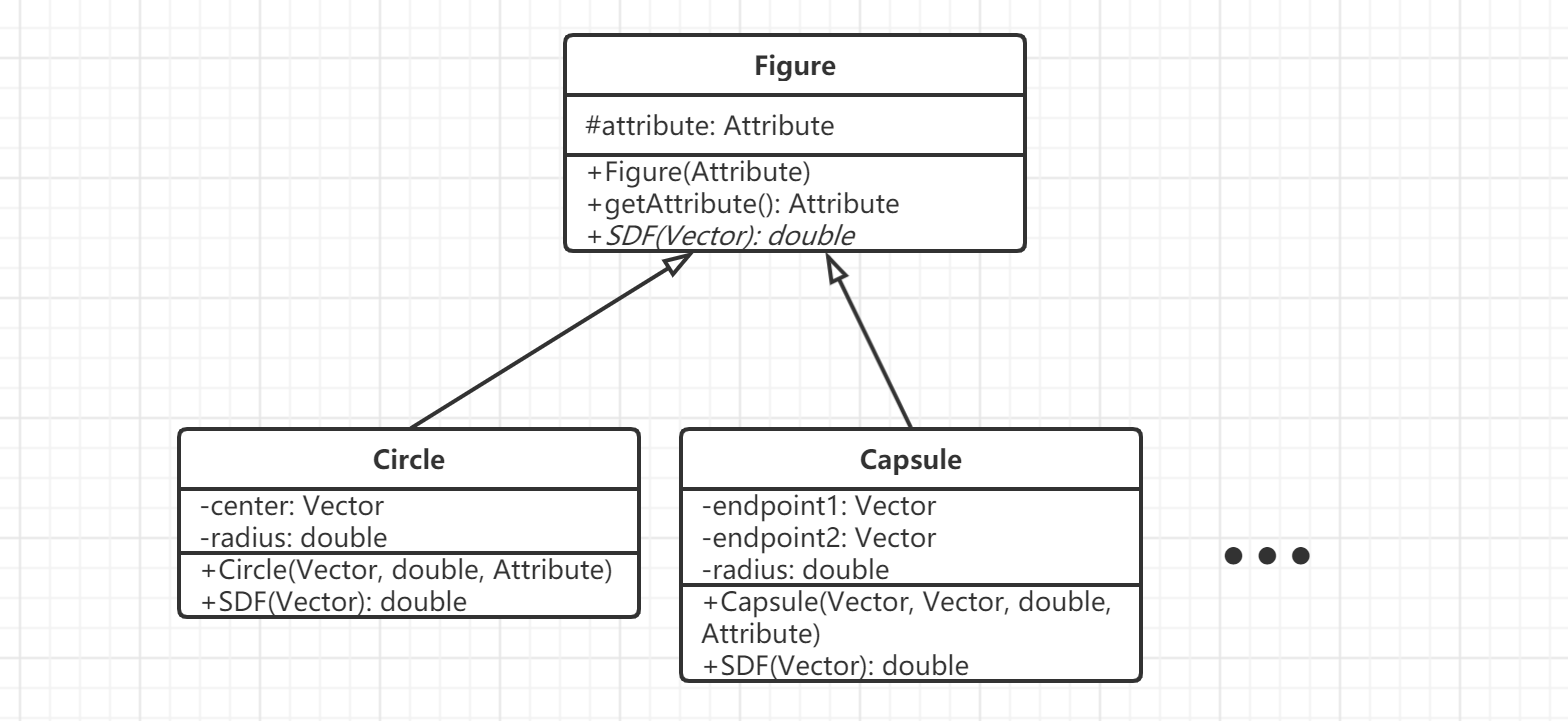
按照上述结构,我们可以重构一下上一篇博文中圆与胶囊的SDF函数:
//父类:所有图形
class Figure
{
public:
//图形的共有属性
typedef struct Attribute
{
Color color;
}Attribute;
protected:
Attribute attribute;
public:
//构造函数,注意各个子类图形在构造时需调用父类的构造函数
Figure(Attribute attribute)
{
this->attribute = attribute;
}
Attribute getAttribute()
{
return attribute;
}
//SDF接口
virtual double SDF(Vector pos) = 0;
};
//圆,继承图形
class Circle : public Figure
{
private:
Vector center; //圆心
double radius; //半径
public:
//构造函数,注意需调用父类构造函数
Circle(Vector center, double radius, Attribute attribute) : Figure(attribute)
{
this->center = center;
this->radius = radius;
}
//实现计算SDF的接口
double SDF(Vector pos)
{
return (pos - center).module() - radius;
}
};
//胶囊,继承图形
class Capsule : public Figure
{
private:
Vector endpoint1; //端点1
Vector endpoint2; //端点2
double radius; //半径
public:
Capsule(Vector endpoint1, Vector endpoint2, double radius, Attribute attribute) : Figure(attribute)
{
this->endpoint1 = endpoint1;
this->endpoint2 = endpoint2;
this->radius = radius;
}
double SDF(Vector pos)
{
Vector V1 = endpoint2 - endpoint1;
Vector V2 = pos - endpoint1;
if (V1 * V2 <= 0)
return V2.module() - radius;
else
{
Vector V3 = pos - endpoint2;
if (V1 * V3 >= 0)
return V3.module() - radius;
else
return fabs(V1.normalVector() * V2) - radius;
}
}
};
这样让所有图形继承一个父类的好处就是,绘图函数不需要针对特定的图形,而只需根据父类 Figure 及其方法即可。
绘图函数可以这样写:(伪代码)
void draw(Figure figure)
{
for (int i = 0; i < width; i++)
for (int j = 0; j < height; j++)
if (figure.SDF() < 0) setPixel();
}
基本图形
下面我们将列举一些常用的基本图形的符号距离函数。(注:下面类的实现中均省略构造函数)
基本图形SDF的部分算法与图片来源于 Inigo Quilez :: fractals, computer graphics, mathematics, shaders, demoscene and more,作者在学习时也是参考的这个网站所列举的实现。
圆
推导见上一篇中 圆的有符号距离场。

class Circle : public Figure
{
private:
Vector center; //圆心
double radius; //半径
public:
//实现计算SDF的接口
double SDF(Vector pos)
{
return (pos - center).module() - radius;
}
};
线段(胶囊)
推导见上一篇中 直线(胶囊)的有符号距离场。

class Capsule : public Figure
{
private:
Vector endpoint1; //端点1
Vector endpoint2; //端点2
double radius; //半径
public:
double SDF(Vector pos)
{
Vector V1 = endpoint2 - endpoint1;
Vector V2 = pos - endpoint1;
if (V1 * V2 <= 0)
return V2.module() - radius;
else
{
Vector V3 = pos - endpoint2;
if (V1 * V3 >= 0)
return V3.module() - radius;
else
return fabs(V1.normalVector() * V2) - radius;
}
}
};
变宽胶囊
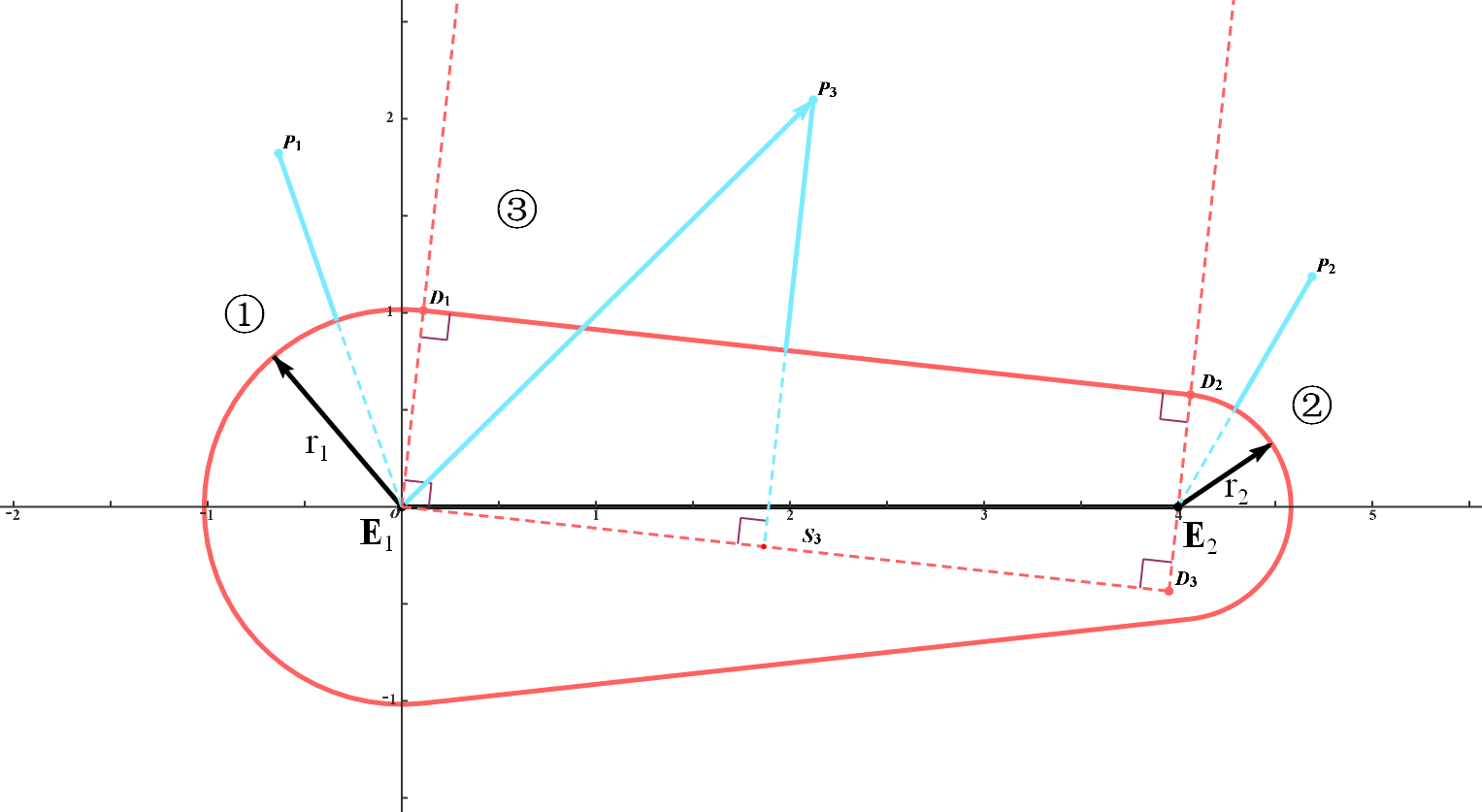
变宽胶囊指两端半径不同,宽度沿线段均匀变化的胶囊的变种,如图:

可知变宽胶囊有6个自由度:两个端点占4个、两端的半径占2个。此图形可以使用四个量确定:端点 $\boldsymbol E_1,\boldsymbol E_2$、半径 $r_1,r_2$。
为了便于计算,我们将图形旋转平移,使得 $\boldsymbol E_1$ 位于原点,$\boldsymbol E_2$ 位于 $x$ 轴正半轴,对应的平移矢量为 $-\boldsymbol E_1$,旋转角度为 $\alpha=-\mathrm{atan2}(\boldsymbol E_{2y}-\boldsymbol E_{1y},\boldsymbol E_{2x}-\boldsymbol E_{1x})$,如图
令 $d_x=\boldsymbol E_{2x}-\boldsymbol E_{1x},d_y=\boldsymbol E_{2y}-\boldsymbol E_{1y}$,则
\[\cos\alpha=\frac{d_x}{\sqrt{d_x^2+d_y^2}},\sin\alpha=-\frac{d_y}{\sqrt{d_x^2+d_y^2}}\]与此同时,目标点 $\boldsymbol P$ 的坐标变换为
\[\boldsymbol P'=\left(\begin{matrix} \cos\alpha&-\sin\alpha\\ \sin\alpha&\cos\alpha\\ \end{matrix}\right)(\boldsymbol P-\boldsymbol E_1) =\frac1{\sqrt{d_x^2+d_y^2}}\left(\begin{matrix} d_x&d_y\\ -d_y&d_x\\ \end{matrix}\right)(\boldsymbol P-\boldsymbol E_1)\]从图中容易看出该图形按 $x$ 轴轴对称,于是我们只考虑上半平面的部分,由对称即可得到下半平面。
图中 $E_1D_3$ 平行于图形的上边界 $D_1D_2$,且位于被考察区域外,故可用于区域③中距离的计算。这是 $r_1>r_2$ 的情况下,若 $r_2>r_1$,$E_1D_3$ 就不再位于考察区域外了,故在初始化时建议先将两个端点按半径排好序。
图中
\[\begin{gather} E_1E_2=\|\boldsymbol E_2-\boldsymbol E_1\|\\ E_2D_3=D_2D_3-E_2D_2=E_1D_1-E_2D_2=r_1-r_2\\ \end{gather}\]故
\[\begin{gather} \sin\angle E_2E_1D_3=\frac{E_2D_3}{E_1E_2}=\frac{r_1-r_2}{\|\boldsymbol E_2-\boldsymbol E_1\|}\\ \cos\angle E_2E_1D_3=\sqrt{1-\sin^2\angle E_2E_1D_3} \end{gather}\]令 $a=\sin\angle E_2E_1D_3=\frac{r_1-r_2}{|\boldsymbol E_2-\boldsymbol E_1|},b=\cos\angle E_2E_1D_3=\sqrt{1-a^2}$,可以得到
$E_1D_3$ 的长度为 $b|\boldsymbol E_2-\boldsymbol E_1|$ 方向的单位向量为 $\boldsymbol L=(b,-a)$,其逆时针转90°的单位法向量为 $\boldsymbol N=(a,b)$,类似胶囊SDF函数有
\[f_{uneven\ capsule}(\boldsymbol P)=\left\{\begin{split} &\|\boldsymbol P'-\boldsymbol E_1\|-r_1&(\boldsymbol P'-\boldsymbol E_1)\cdot\boldsymbol L\le0\\ &\|\boldsymbol P'-\boldsymbol E_2\|-r_2&(\boldsymbol P'-\boldsymbol E_1)\cdot\boldsymbol L\ge b\|\boldsymbol E_2-\boldsymbol E_1\|\\ &(\boldsymbol P'-\boldsymbol E_1)\cdot\boldsymbol N-r_1\quad\quad&0<(\boldsymbol P'-\boldsymbol E_1)\cdot\boldsymbol L<b\|\boldsymbol E_2-\boldsymbol E_1\| \end{split}\right.\]算法为:

class UnevenCapsule : public Figure
{
private:
Vector endpoint1;
Vector endpoint2;
double radius1;
double radius2;
public:
double SDF(Vector pos)
{
double dx = endpoint2.x - endpoint1.x;
double dy = endpoint2.y - endpoint1.y;
double h = sqrt(dx * dx + dy * dy);
double cos_ = dx / h;
double sin_ = -dy / h;
Vector E1 = {0, 0};
Vector E2 = {h, 0};
double a = (radius1 - radius2) / h;
double b = sqrt(1 - a * a);
Vector L = {b, -a};
Vector N = {a, b};
pos = pos - endpoint1;
Vector pos_ = {cos_ * pos.x - sin_ * pos.y, fabs(sin_ * pos.x + cos_ * pos.y)};
double jdg = (pos_ - E1) * L;
if (jdg <= 0)
return (pos_ - E1).module() - radius1;
else if (jdg >= b * h)
return (pos_ - E2).module() - radius2;
else
return (pos_ - E1) * N - radius1;
}
};
矩形
矩形有五个自由度:长、宽、中心x、中心y、旋转角度。在这里我们使用三个量表示:中心 $\boldsymbol C$、尺寸 $\boldsymbol S$、旋转角 $\theta$
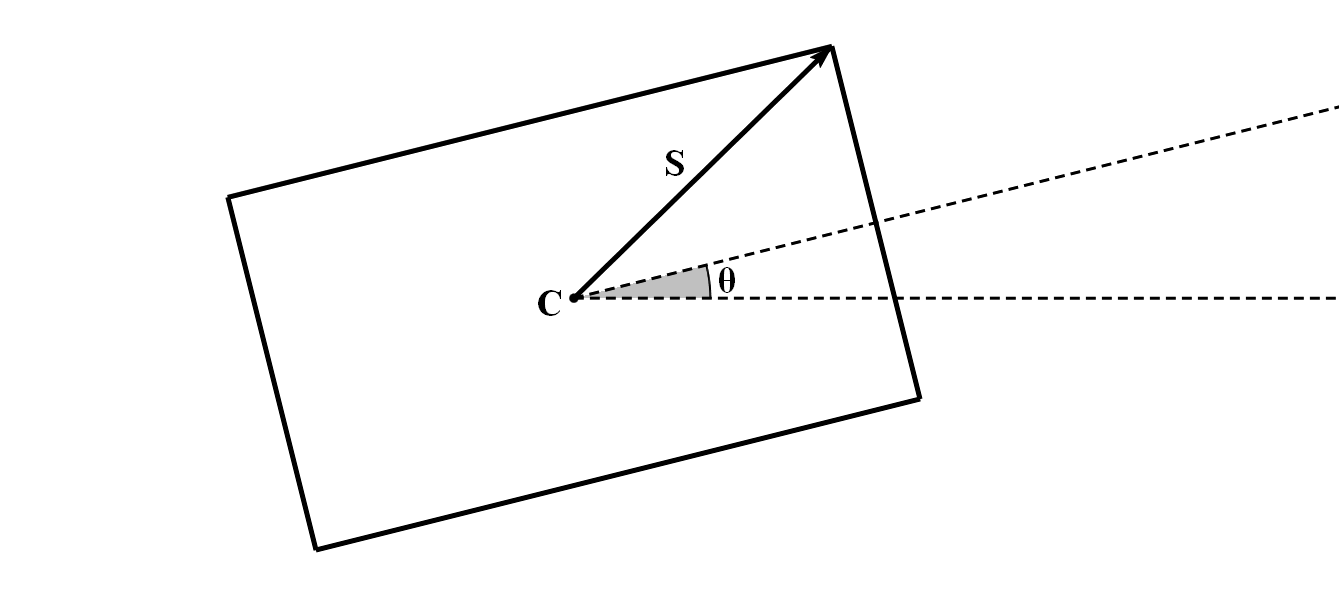
其中中心 $\boldsymbol C$、旋转角 $\theta$ 可以靠坐标的平移和旋转变换使之为 $0$,与此同时,目标点 $\boldsymbol P$ 的坐标变换为
\[\boldsymbol P'=\left(\begin{matrix} \cos\theta&\sin\theta\\ -\sin\theta&\cos\theta\\ \end{matrix}\right)(\boldsymbol P-\boldsymbol C)\]考虑到矩形拥有四等分对称性,我们只考虑第一象限的部分,由对称即可得到其余部分,如图
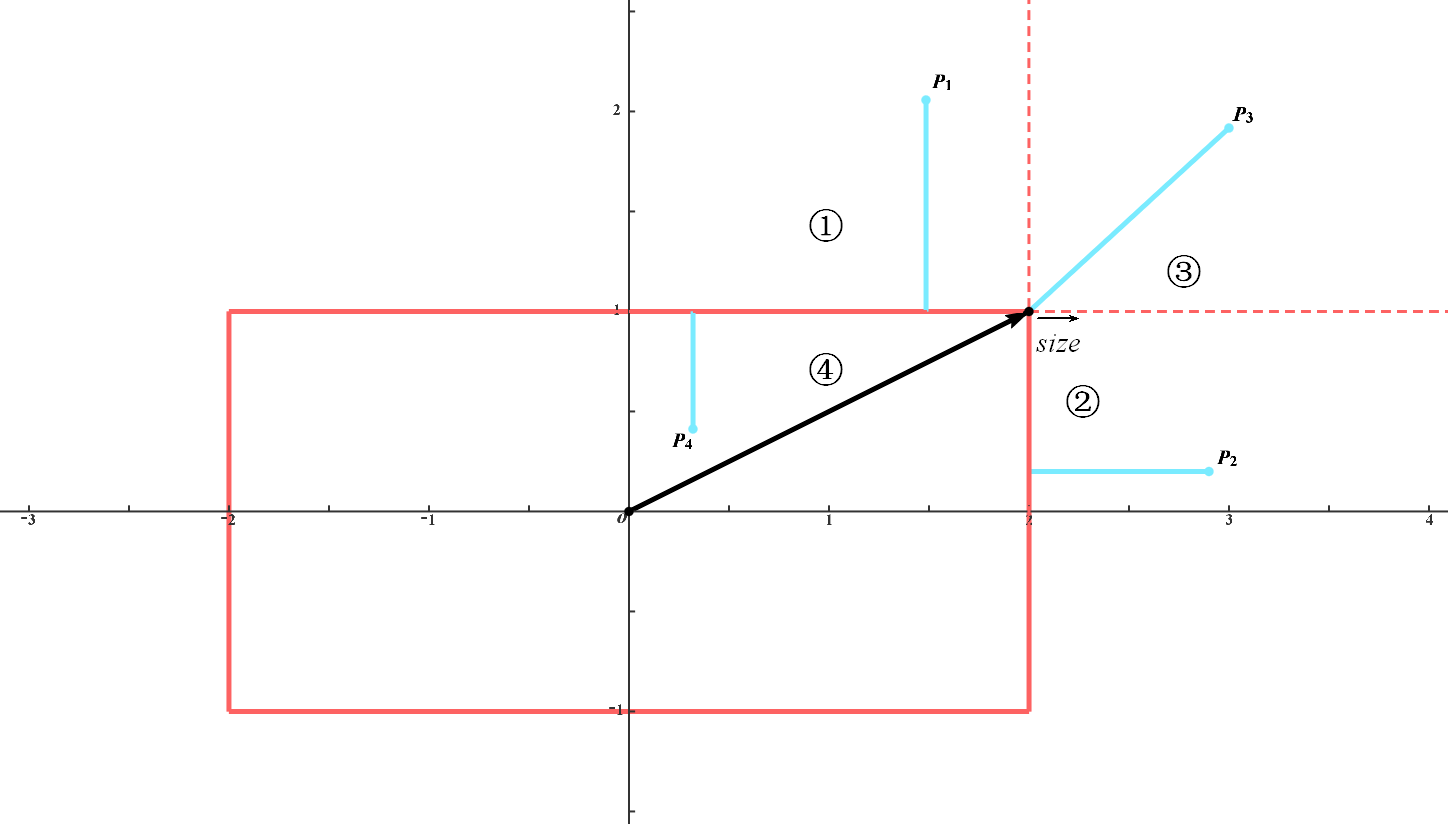
在图中标识出了四个区域,在每个区域中距离的计算方法是不同的,易知
\[f_{Rectangle}(\boldsymbol P)=\left\{\begin{split} &\boldsymbol P'_y-\boldsymbol S_y&\boldsymbol P'\in①\\ &\boldsymbol P'_x-\boldsymbol S_x&\boldsymbol P'\in②\\ &\|\boldsymbol P'-\boldsymbol S\|&\boldsymbol P'\in③\\ &\mathrm{max}\{\boldsymbol P'_x-\boldsymbol S_x,\boldsymbol P'_y-\boldsymbol S_y\}\quad\quad&\boldsymbol P'\in④ \end{split}\right.\]在考虑上各区域的条件
\[f_{Rectangle}(\boldsymbol P)=\left\{\begin{split} &\boldsymbol P'_y-\boldsymbol S_y&\boldsymbol P'_x<\boldsymbol S_x,\boldsymbol P'_y>\boldsymbol S_y\\ &\boldsymbol P'_x-\boldsymbol S_x&\boldsymbol P'_x>\boldsymbol S_x,\boldsymbol P'_y<\boldsymbol S_y\\ &\|\boldsymbol P'-\boldsymbol S\|&\boldsymbol P'_x>\boldsymbol S_x,\boldsymbol P'_y>\boldsymbol S_y\\ &\mathrm{max}\{\boldsymbol P'_x-\boldsymbol S_x,\boldsymbol P'_y-\boldsymbol S_y\}\quad\quad&\boldsymbol P'_x<\boldsymbol S_x,\boldsymbol P'_y<\boldsymbol S_y \end{split}\right.\]算法为:

class Rectangle : public Figure
{
private:
Vector center;
Vector size;
double theta;
public:
double SDF(Vector pos)
{
double cos_ = cos(theta);
double sin_ = sin(theta);
pos = pos - center;
Vector pos_ = {fabs(cos_ * pos.x + sin_ * pos.y), fabs(-sin_ * pos.x + cos_ * pos.y)};
if (pos_.x > size.x)
{
if (pos_.y > size.y)
return (pos_ - size).module();
else
return pos_.x - size.x;
}
else
{
if (pos_.y > size.y)
return pos_.y - size.y;
else
return max(pos_.y - size.y, pos_.x - size.x);
}
}
};
三角形
三角形显然是由三个顶点 $\boldsymbol V_1,\boldsymbol V_2,\boldsymbol V_3$ 所决定的,如图
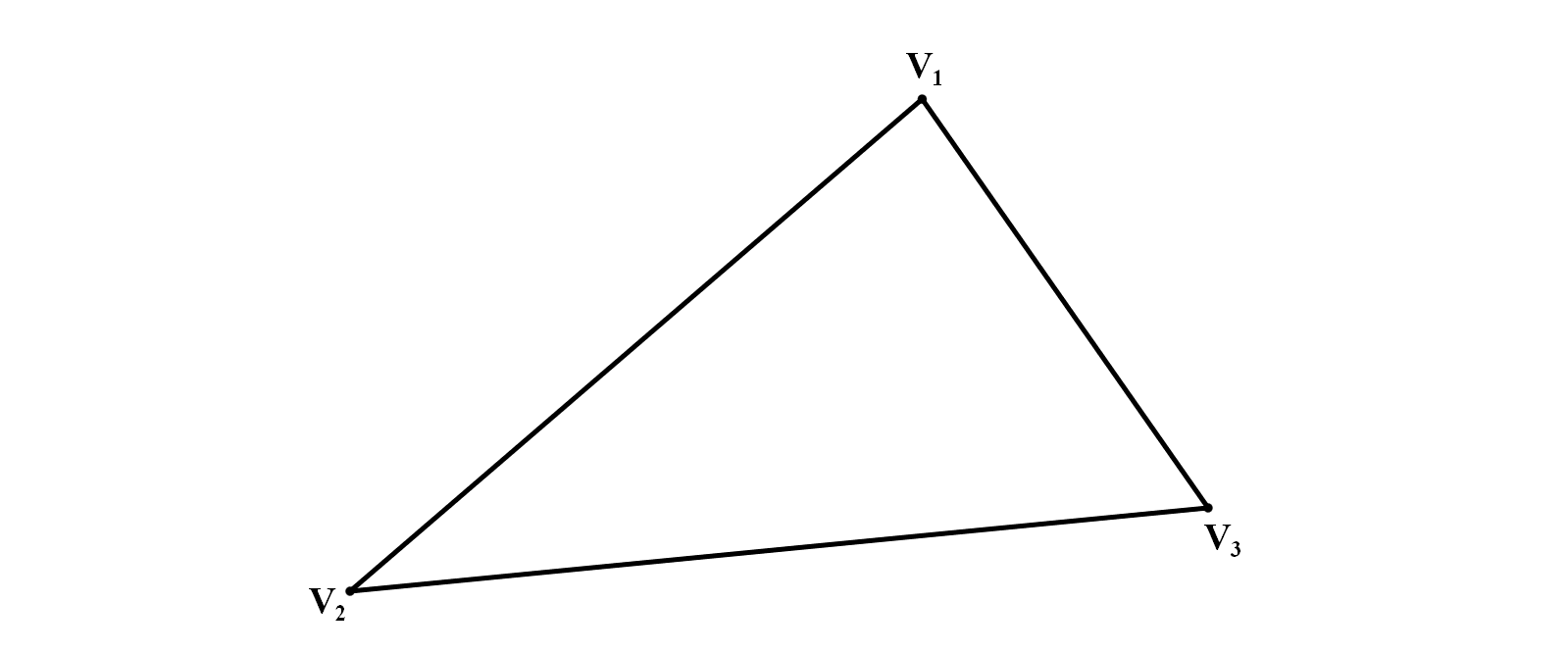
为计算三角形的SDF,可以将三条边单独考虑,求出目标点到三条边的距离的最小值,即为SDF的绝对值。求一点到线段的距离在胶囊图形已经讲过。
剩下的问题在于:如何判断目标点是不是在三角形内部?
一个可行的方法是利用凸多边形与叉乘的性质。
沿一个方向遍历凸多边形的所有边,则对于位于凸多边形内部的点,它总在被考察有向边的同一侧。而三角形必然是一个凸多边形。
例如上图中,三角形内部的点位于 $V_1V_2,V_2V_3,V_3V_1$ 的左侧。
根据右手定则,若点 $P$ 在有向线段 $V_iV_j$ 左侧,则
\[[(\boldsymbol V_j-\boldsymbol V_i)\times(\boldsymbol P-\boldsymbol V_i)].z>0\]反之
\[[(\boldsymbol V_j-\boldsymbol V_i)\times(\boldsymbol P-\boldsymbol V_i)].z<0\]综上,在三角形中,令
\[\begin{gather} \boldsymbol L_1=\boldsymbol V_2-\boldsymbol V_1,\quad\boldsymbol L_2=\boldsymbol V_3-\boldsymbol V_2,\quad\boldsymbol L_3=\boldsymbol V_1-\boldsymbol V_3\\ \boldsymbol P_1=\boldsymbol P-\boldsymbol V_1,\quad\boldsymbol P_2=\boldsymbol P-\boldsymbol V_2,\quad\boldsymbol P_3=\boldsymbol P-\boldsymbol V_3 \end{gather}\]若点 $P$ 在三角形内部,则
\[\boldsymbol L_{1x}\boldsymbol P_{1y}-\boldsymbol L_{1y}\boldsymbol P_{1x},\quad\boldsymbol L_{2x}\boldsymbol P_{2y}-\boldsymbol L_{2y}\boldsymbol P_{2x},\quad\boldsymbol L_{3x}\boldsymbol P_{3y}-\boldsymbol L_{3y}\boldsymbol P_{3x}\]三者同号。算法为:

class Triangle : public Figure
{
private:
Vector vertex1;
Vector vertex2;
Vector vertex3;
public:
double SDF(Vector pos)
{
double d1 = segmentSDF(vertex1, vertex2, pos);
double d2 = segmentSDF(vertex2, vertex3, pos);
double d3 = segmentSDF(vertex3, vertex1, pos);
double d = min(min(d1, d2), d3);
if ((((vertex2.x - vertex1.x) * (pos.y - vertex1.y) - (vertex2.y - vertex1.y) * (pos.x - vertex1.x) > 0) &&
((vertex3.x - vertex2.x) * (pos.y - vertex2.y) - (vertex3.y - vertex2.y) * (pos.x - vertex2.x) > 0) &&
((vertex1.x - vertex3.x) * (pos.y - vertex3.y) - (vertex1.y - vertex3.y) * (pos.x - vertex3.x) > 0)) ||
(((vertex2.x - vertex1.x) * (pos.y - vertex1.y) - (vertex2.y - vertex1.y) * (pos.x - vertex1.x) < 0) &&
((vertex3.x - vertex2.x) * (pos.y - vertex2.y) - (vertex3.y - vertex2.y) * (pos.x - vertex2.x) < 0) &&
((vertex1.x - vertex3.x) * (pos.y - vertex3.y) - (vertex1.y - vertex3.y) * (pos.x - vertex3.x) < 0)))
return -d;
else
return d;
}
};
多边形
在上篇博文中我们提到过使用扫描线算法绘制多边形,那么我们来看看怎样构建多边形的SDF。
多边形由 $n$ 个顶点 $V_1,V_2,\cdots,V_n$ 所描述,其中 $n\ge3$。
有了三角形SDF的经验,我们知道,多边形的SDF的绝对值即为目标点到多边形所有边的距离的最小值。问题来到了怎样判断一个点是不是在多边形内。在扫描线算法中,两两一对的交点所构造的线段位于图形的内部。这说明若一个点位于图形的内部,则在与它同高的扫描线与图形的交点中有奇数个位于此点的同一侧。如图
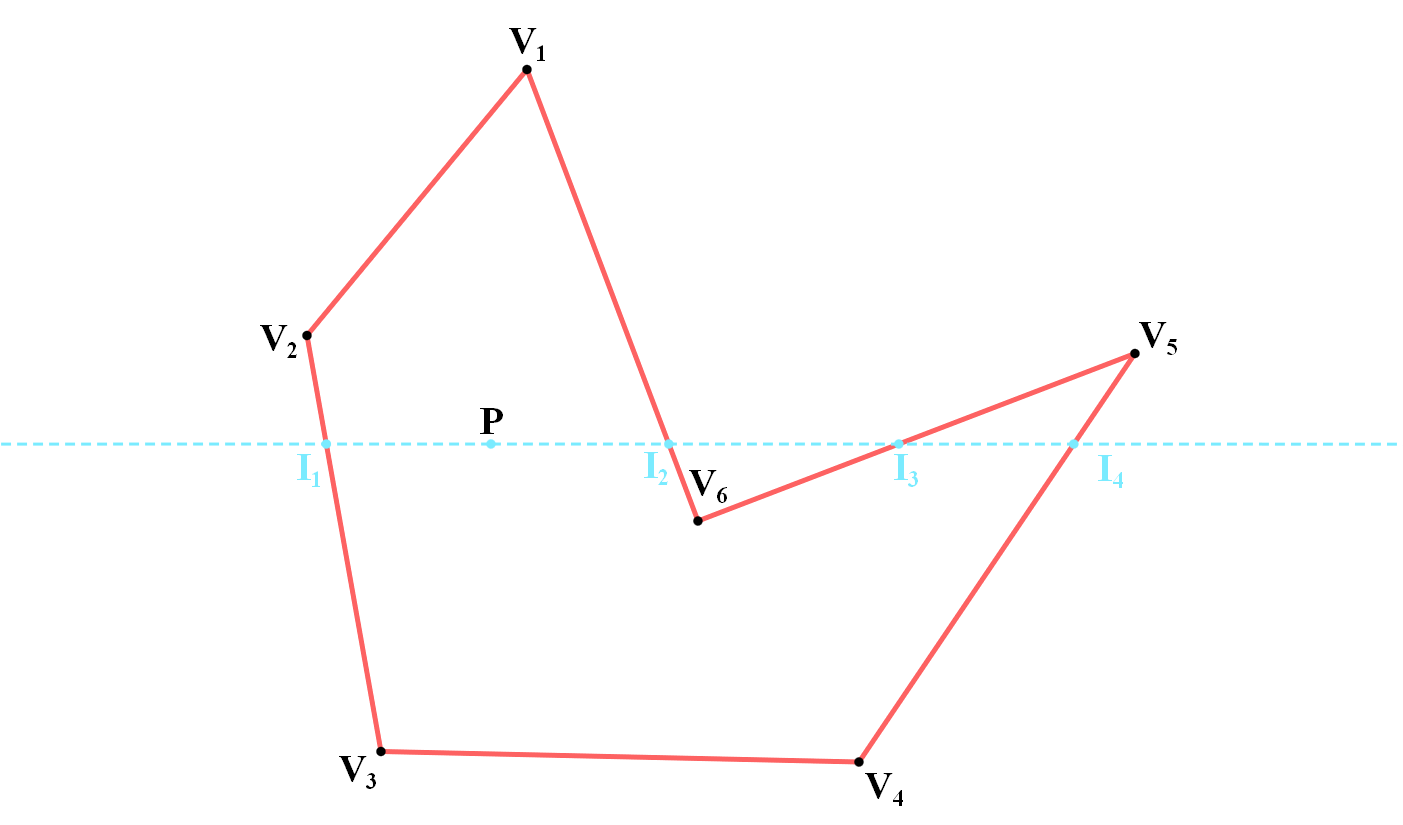
可见图中 $P$ 点左侧有1个交点,右侧有3个交点,都为奇数。由此我们的目的很明确了:计算出位于目标点左侧的交点的个数,以此来判断目标点是否在多边形内部。
这个问题可以分解为两个子问题:
- 判断一条边是否与目标点高度的扫描线有交点
- 判断交点在目标点的哪一侧
第一个问题容易解决,判断 $P$ 的纵坐标是否在这条边的两个端点的纵坐标之间即可。
第二个问题我们需要反过来考虑,可以判断目标点在交点的哪一侧,即目标点在这条边的哪一侧。在三角形SDF的推导中,我们提到利用向量叉乘判断点在有向边的哪一侧,我们沿用这个方法。但是注意,在有向边向上的时候,它的左侧才与屏幕的左侧一致,若有向边向下,它的右侧才是屏幕的左侧。
写成公式即为
\[\begin{gather} \boldsymbol E_1=\boldsymbol V_2-\boldsymbol V_1,\quad\boldsymbol E_2=\boldsymbol V_3-\boldsymbol V_2,\cdots,\boldsymbol E_n=\boldsymbol V_1-\boldsymbol V_n\\ \boldsymbol W_1=\boldsymbol P-\boldsymbol V_1,\quad\boldsymbol W_2=\boldsymbol P-\boldsymbol V_2,\cdots,\boldsymbol W_n=\boldsymbol P-\boldsymbol V_n\\ f_{polygon}(\boldsymbol P)=(-1)^j\min\{d(P,V_1V_2),d(P,V_2V_3),\cdots,d(P,V_nV_1)\}\\ j=\sum_{i=1}^n((\boldsymbol E_i\times\boldsymbol W_i).z>0\land \boldsymbol E_{iy}>\boldsymbol W_{iy}\land\boldsymbol W_{iy}>0)\lor((\boldsymbol E_i\times\boldsymbol W_i).z<0\land \boldsymbol E_{iy}<\boldsymbol W_{iy}\land\boldsymbol W_{iy}<0) \end{gather}\]算法为

class Polygon : public Figure
{
private:
Vector* vertex;
int vertexNummber;
public:
double SDF(Vector pos)
{
Vector E, W;
double d = 1e10;
int s = 1;
for (int i = 0, j; i < vertexNummber; i++)
{
j = (i + 1) % vertexNummber;
d = min(d, segmentSDF(vertex[i], vertex[j], pos));
if ((vertex[j].y >= pos.y && vertex[i].y < pos.y &&
(vertex[j].x - vertex[i].x) * (pos.y - vertex[i].y) -
(vertex[j].y - vertex[i].y) * (pos.x - vertex[i].x) > 0) ||
(vertex[i].y >= pos.y && vertex[j].y < pos.y &&
(vertex[j].x - vertex[i].x) * (pos.y - vertex[i].y) -
(vertex[j].y - vertex[i].y) * (pos.x - vertex[i].x) < 0))
s *= -1;
}
return s * d;
}
};
扇形
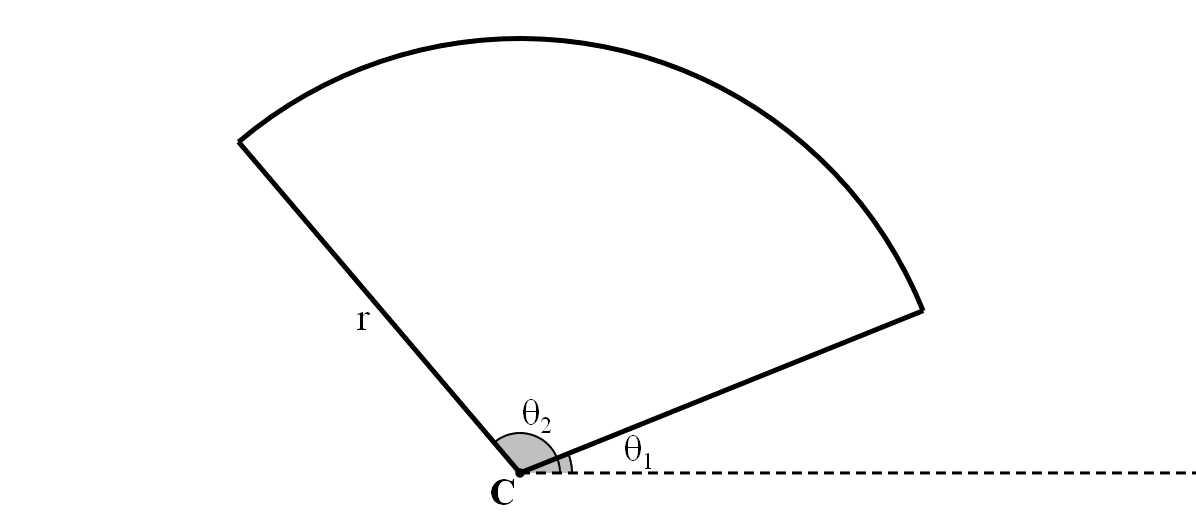
扇形也是常用的图形之一,它由4个量表征:圆心 $\boldsymbol C$,半径 $r$ 以及起始角度 $\theta_1,\theta_2$,如图
处理它的SDF仍需根据对称性将其平移旋转:圆心与坐标原点重合,角平分线与 $x$ 轴重合。则平移向量为 $-\boldsymbol C$,旋转角为 $-\frac{\theta_1+\theta_2}2$
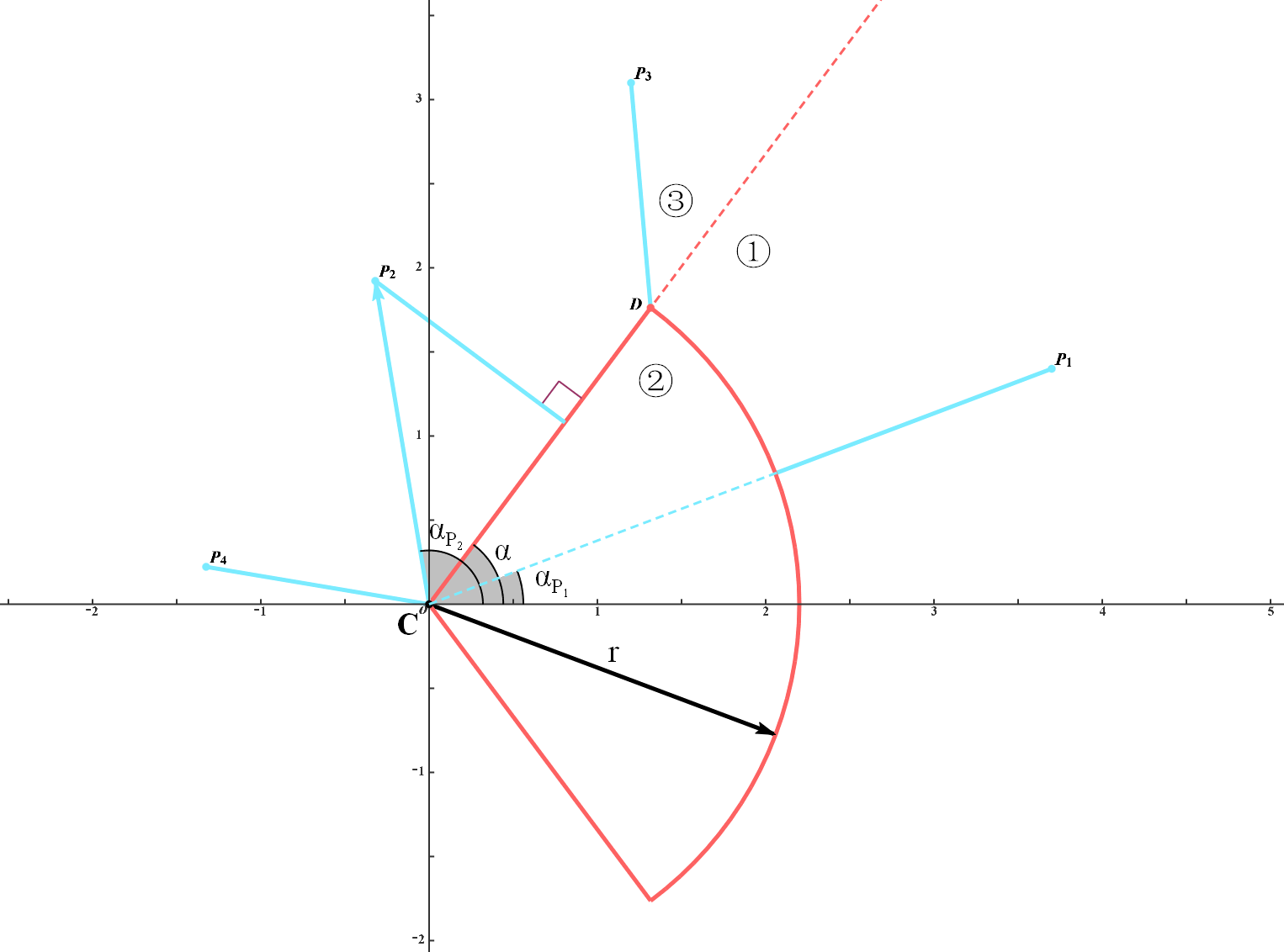
$\boldsymbol P’$ 的坐标与前文一样变换。由于扇形的轴对称性,我们只需考察上半平面即可。沿上半平面中的径向边与圆弧可将被考察区域分为三部分。
在①中,SDF即为到圆弧的距离,也就是到圆心的距离减去半径。
\[f_{pie}=\|\boldsymbol P'\|-r\quad\quad\boldsymbol P'\in①\]在②中,SDF为到圆弧的距离与到径向边的距离中较小的那个的相反数。
\[f_{pie}=\mathrm{max}\{\|\boldsymbol P'\|-r,-d(P',CD)\}\quad\quad\boldsymbol P'\in②\]在③中,SDF为到径向边的距离
\[f_{pie}=d(P',CD)\quad\quad\boldsymbol P'\in③\]算法为:

class Pie : public Figure
{
private:
Vector center;
double radius;
double theta1;
double theta2;
public:
double SDF(Vector pos)
{
double cos_ = cos((theta1 + theta2) / 2);
double sin_ = sin((theta1 + theta2) / 2);
Vector O = {0, 0};
Vector D = {radius * cos((theta2 - theta1) / 2), radius * sin((theta2 - theta1) / 2)};
pos = pos - center;
Vector pos_ = {cos_ * pos.x + sin_ * pos.y, fabs(-sin_ * pos.x + cos_ * pos.y)};
double l = pos_.module();
if (D.x * pos_.y - D.y * pos_.x > 0)
return segmentSDF(O, D, pos_);
else if (l >= radius)
return l - radius;
else
return max(l - radius, -segmentSDF(O, D, pos_));
}
};
弧
与扇形有关系的有另一个图形——圆弧,它由5个量表示:圆心 $\boldsymbol C$,弧半径 $r_1$,弧半宽 $r_2$ 以及起始角度 $\theta_1,\theta_2$,如图
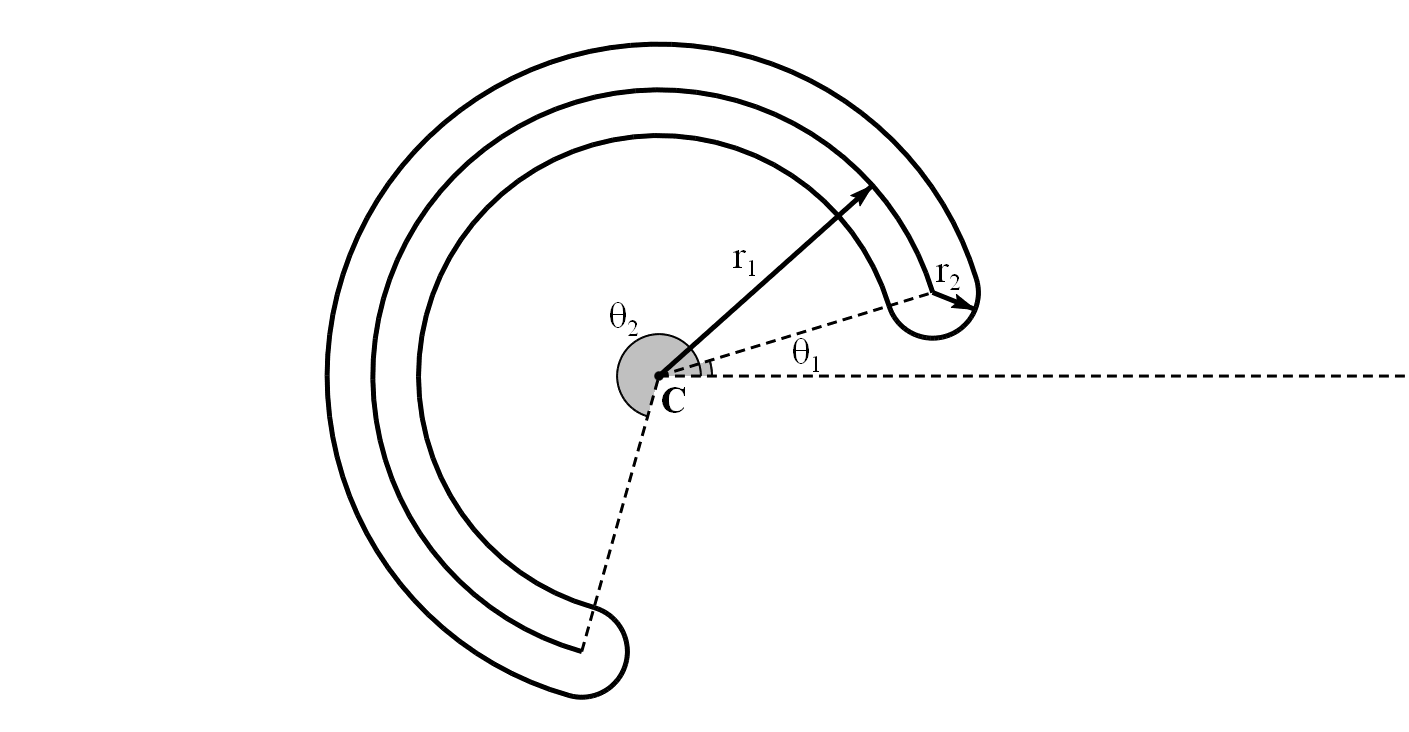
它的SDF与扇形类似,有一点小改动
在①或②中,SDF即为到圆弧的距离减去半宽
\[f_{pie}=\|\|\boldsymbol P'\|-r_1\|-r_2\quad\quad\boldsymbol P'\in①\cup②\]在③中,SDF为到弧的端点的距离减去半宽
\[f_{pie}=\|\boldsymbol P'-\boldsymbol D\|-r_2\quad\quad\boldsymbol P'\in③\]算法为:

class Arc : public Figure
{
private:
Vector center;
double radius1;
double radius2;
double theta1;
double theta2;
public:
double SDF(Vector pos)
{
double cos_ = cos((theta1 + theta2) / 2);
double sin_ = sin((theta1 + theta2) / 2);
Vector O = {0, 0};
Vector D = {radius1 * cos((theta2 - theta1) / 2), radius1 * sin((theta2 - theta1) / 2)};
pos = pos - center;
Vector pos_ = {cos_ * pos.x + sin_ * pos.y, fabs(-sin_ * pos.x + cos_ * pos.y)};
double l = pos_.module();
if (D.x * pos_.y - D.y * pos_.x > 0)
return (pos_ - D).module() - radius2;
else
return fabs(l - radius1) - radius2;
}
};
椭圆
为求椭圆SDF,关键在于找到椭圆上哪一点到目标点距离最短,这不是那么容易的。
考虑进行平移和旋转变换,我们只需考虑一个标准的中心在原点,焦点在 $x$ 轴上的椭圆,满足
\[\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\]由对称性,只需考虑第一象限。容易想到,当目标点到椭圆上一点的连线与椭圆过这点的切线垂直时,这点就是我们要找的最近点,可列方程
\[\left\{\begin{split} &\frac{y_p-y}{x_p-x}\frac{b^2x}{a^2y}=1\\ &y=\frac ba\sqrt{a^2-x^2} \end{split}\right.\]最终会得到一个四次方程。。。
\[\frac{(a^2-b^2)^2}{a^2}x^4-2(a^2-b^2)x_px^3+(b^2y_p^2+a^2x_p^2-(a^2-b^2)^2)x^2+2a^2(a^2-b^2)x_px-a^4x_p=0\]参考椭圆的参数方程,令 $x=a\cos\theta,u=\cos\theta$
\[(a^2-b^2)^2u^4-2a(a^2-b^2)x_pu^3+(b^2y_p^2+a^2x_p^2-(a^2-b^2)^2)u^2+2a(a^2-b^2)x_pu-a^2x_p=0\]再令 $m=\frac{a}{a^2-b^2}x_p,n=\frac{b}{a^2-b^2}y_p$
\[u^4-2mu^3+(m^2+n^2-1)u^2+2mu-m^2\]四次方程的求解非常复杂…(可以参考:Quartic Equation – from Wolfram MathWorld,distance to an ellipse - iquilezles),最后我们直接给出算法:

class Ellipse : public Figure
{
private:
Vector center;
double a;
double b;
double theta;
public:
double SDF(Vector pos)
{
double cos_ = cos(theta);
double sin_ = sin(theta);
pos = pos - center;
Vector p = {fabs(cos_ * pos.x + sin_ * pos.y), fabs(-sin_ * pos.x + cos_ * pos.y)};
double a = this->a, b = this->b;
if(p.x > p.y)
{
swap(p.x, p.y);
swap(a, b);
}
double l = b * b - a * a;
double m = a * p.x / l;
double m2 = m * m;
double n = b * p.y / l;
double n2 = n * n;
double c = (m2 + n2 - 1.0) / 3.0;
double c3 = c * c * c;
double q = c3 + m2 * n2 * 2.0;
double d = c3 + m2 * n2;
double g = m + m * n2;
double co;
if( d < 0.0 )
{
double h = acos(q / c3) / 3.0;
double s = cos(h);
double t = sin(h) * sqrt(3.0);
double rx = sqrt(-c * (s + t + 2.0) + m2);
double ry = sqrt(-c * (s - t + 2.0) + m2);
co = (ry + (l > 0 ? 1 : -1) * rx + fabs(g) / (rx * ry) - m) / 2.0;
}
else
{
double h = 2.0 * m * n * sqrt(d);
double s = (q + h > 0 ? 1 : -1) * pow(fabs(q + h), 1.0 / 3.0);
double u = (q - h > 0 ? 1 : -1) * pow(fabs(q - h), 1.0 / 3.0);
double rx = -s - u - c * 4.0 + 2.0 * m2;
double ry = (s - u) * sqrt(3.0);
double rm = sqrt(rx * rx + ry * ry);
co = (ry / sqrt(rm - rx) + 2.0 * g / rm - m) / 2.0;
}
Vector r = {a * co, b * sqrt(1 - co * co)};
return (r - p).module() * (p.y - r.y > 0 ? 1 : -1);
}
};
二阶贝塞尔曲线
定义与推导参考 二阶贝塞尔曲线与 cc.Bezier - 简书
求其SDF与求椭圆SDF类似考虑,求出切线垂直点,最后是一个三次方程,解它也比较困难,参考 Cubic Equation – from Wolfram MathWorld
直接给出算法:

class QuadraticBezier : public Figure
{
private:
Vector A;
Vector B;
Vector C;
public:
double SDF(Vector pos)
{
Vector a = B - A;
Vector b = A - B * 2.0 + C;
Vector c = a * 2.0;
Vector d = A - pos;
double kk = 1.0 / (b * b);
double kx = kk * (a * b);
double ky = kk * (2.0 * (a * a) + (d * b)) / 3.0;
double kz = kk * (d * a);
double p = ky - kx * kx;
double p3 = p * p * p;
double q = kx * (2.0 * kx * kx - 3.0 * ky) + kz;
double h = q * q + 4.0 * p3;
double res = 0.0;
if(h >= 0)
{
h = sqrt(h);
double x = (h - q) / 2.0;
double y = (-h - q) / 2.0;
double u = (x > 0 ? 1 : -1) * pow(fabs(x), 1.0 / 3.0);
double v = (y > 0 ? 1 : -1) * pow(fabs(y), 1.0 / 3.0);
double t = u + v - kx;
t = (t < 0 ? 0 : (t > 1 ? 1 : t));
Vector e = d + (c + b * t) * t;
res = e * e;
}
else
{
double z = sqrt(-p);
double v = acos(q / (p * z * 2.0)) / 3.0;
double m = cos(v);
double n = sin(v) * sqrt(3);
double x = (m + m) * z - kx;
x = (x < 0 ? 0 : (x > 1 ? 1 : x));
double y = (-n - m) * z - kx;
y = (y < 0 ? 0 : (y > 1 ? 1 : y));
Vector e = d + (c + b * x) * x;
Vector f = d + (c + b * y) * y;
res = min(e * e, f * f);
}
return sqrt(res);
}
};
更多
更多其他图形请前往 Inigo Quilez :: fractals, computer graphics, mathematics, shaders, demoscene and more 探索。
基本操作
基本操作即可以对所有图形所作的操作,即为可以在父类 Figure 中完成的操作,本文中介绍两种:圆化,环化。
圆化




圆化意为将图形中原来的转角变成圆弧,例如将矩形变成圆角矩形。实现也非常简单,将SDF减去圆化半径即可。
为实现此操作,在 Figure::Attribute 中加入属性 double roundedRadius;,变换函数:
double rSDF(Vector pos)
{
return SDF(pos) - attribute.roundedRadius;
}
环化
环化意为以原来图形的边界形成环,例如将矩形变成矩形框。实现为:取SDF的绝对值减去环化半径。




为实现此操作,在 Figure::Attribute 中加入属性 double annularRadius;,变换函数:
double aSDF(Vector pos)
{
return fabs(SDF(pos)) - attribute.annularRadius;
}
代码
本节代码请查看:🔗Github: JeffreyXiang/DrawWithCpp
总结
本章我们给出了许多基本图形的SDF,并介绍了两个基本操作来拓展他们的应用,后续这些基本图形元素将组成我们的图片。求解过程中,我们运用(复习)了一些解析几何与向量的知识,并了解了一些高次方程的解法(虽然我还是不会)。
预告
下一章我将介绍如何使用今天所编写的基本图形合成更复杂的图形——构造实体几何(CSG)。
