前言
在本篇文章中,我将介绍几种绘画直线和圆的算法。
Bresenham 算法
Bresenham算法是一种非常经典的高效率绘画直线和圆的算法。
此算法的基本思路是:以可能被填充的两个像素的中心与直线的距离谁近为依据,利用此前已绘制的像素的信息,递推得下一个像素的位置,从而大量减少计算。
Bresenham 画直线算法
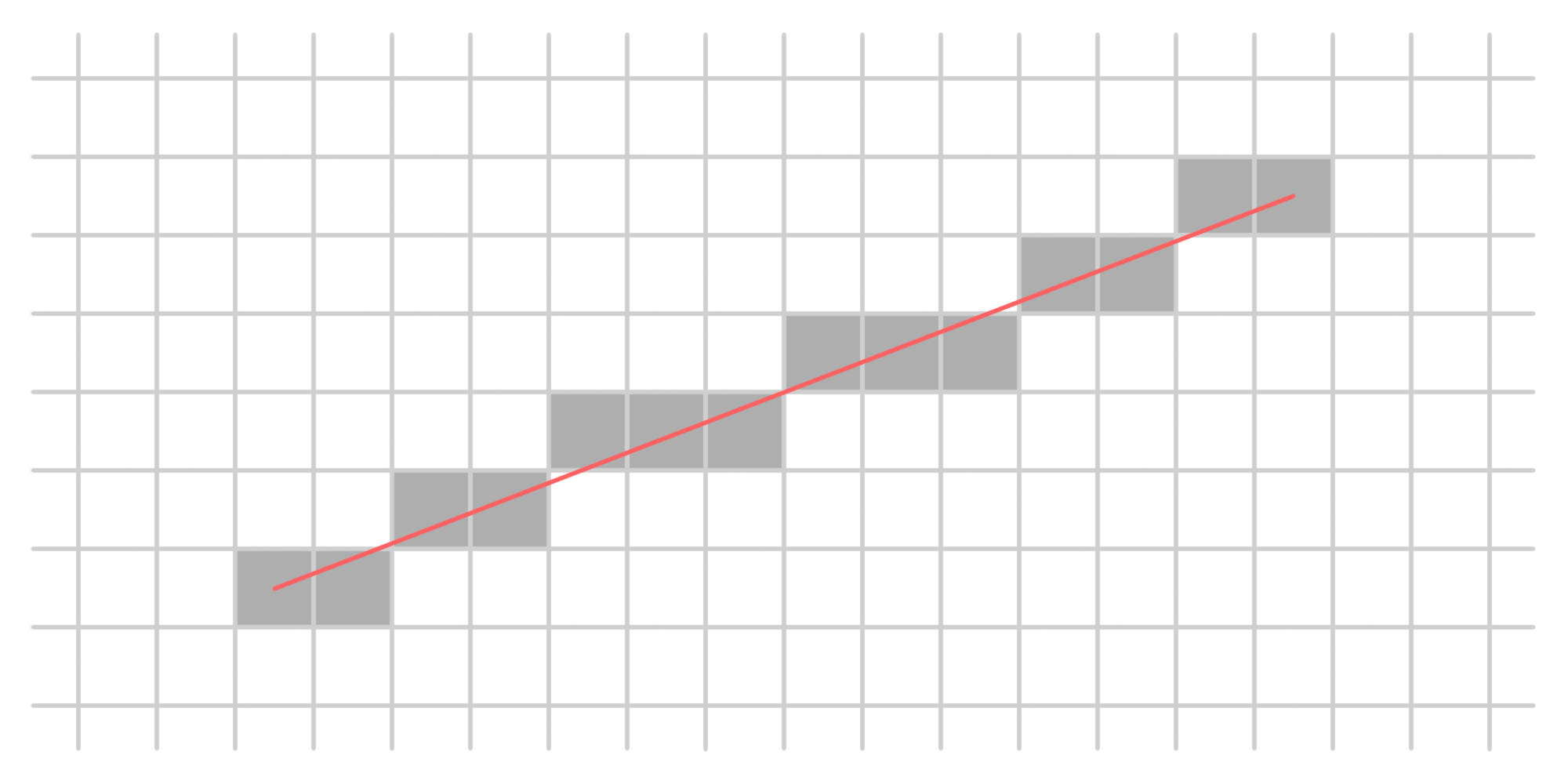
效果如图。先考虑直线的斜率在 0 到 1 之间的情况,即上图中的情况。约定从左向右填充,此时若已知 $(x, y)$ 像素是上一个被填充的像素,则下一个像素只可能为 $(x+1, y)$ 或 $(x+1, y+1)$。
我们将其中一部分放大,并加上判据辅助线。
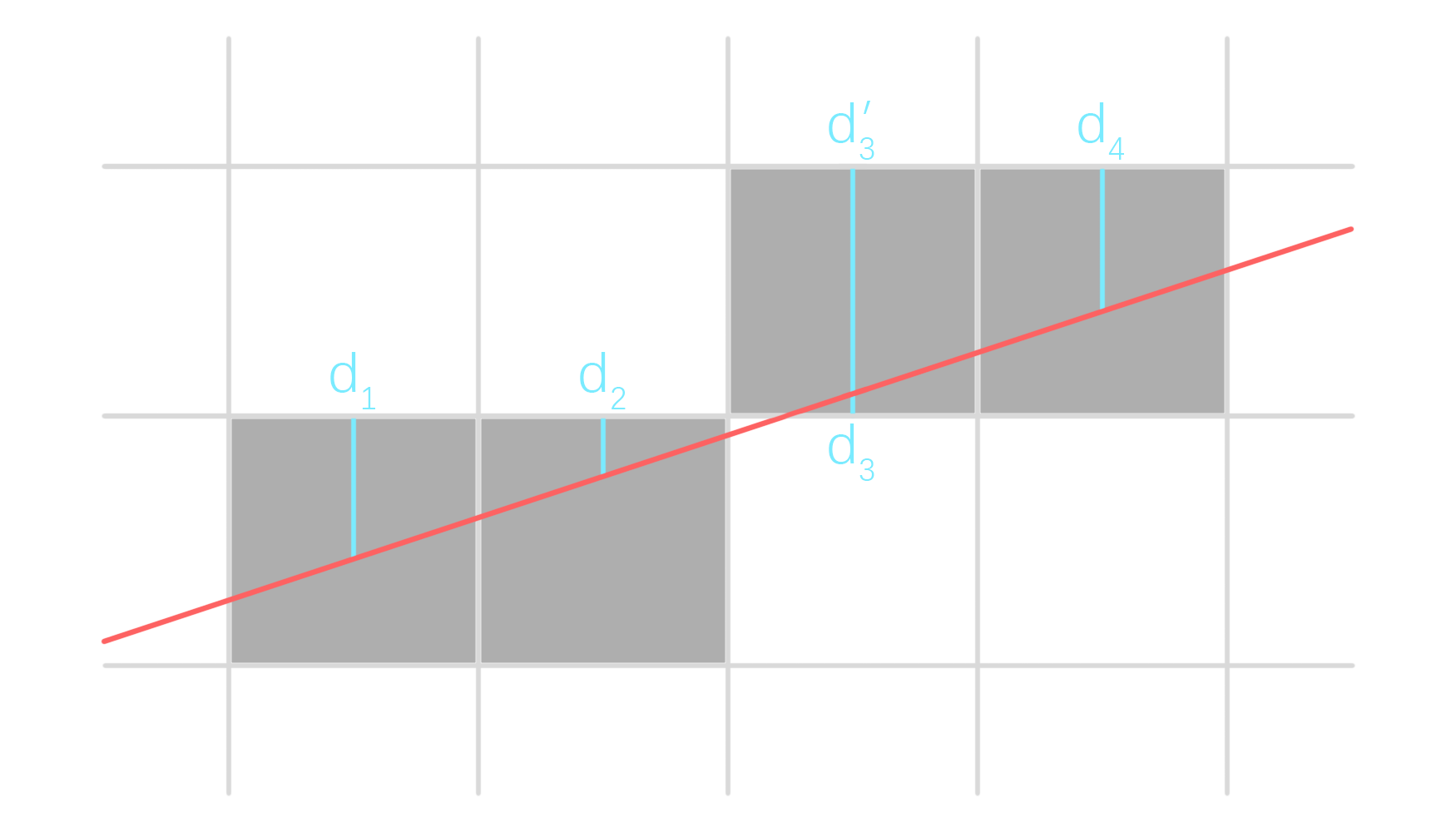
令 $y_x$ 为横坐标为 $x$ 的像素对应的纵坐标值。
由图可知,判断 $(x+1,y_x)$ 和 $(x+1,y_x+1)$ 中哪一个像素被填充取决于这两个像素的中点 $(x+1,y_x+0.5)$ 在目标直线之上还是目标直线之下,即 $d\le0$ 还是 $d>0$(也可以是 $d<0$ 与 $d\ge0$)。若 $d\le0$ 则填 $(x+1,y_x)$,若 $d>0$ 则填 $(x+1,y_x+1)$。
设横坐标 $x$ 的像素填充时算出的中点到目标直线竖直距离为 $d_x$。分情况得递推式
若 $d_x\le0$,说明上一个被填充的像素为 $(x,y_{x-1})$,$d_x$计算为 $(x,y_{x-1}+0.5)$ 到目标直线的竖直距离。则 $d_{x+1}$ 计算为 $(x+1,y_{x}+0.5)$ 即 $(x+1,y_{x-1}+0.5)$ 到目标直线的竖直距离
\[d_{x+1}=d_x+k=d_x+\frac{y_2-y_1}{x_2-x_1}\]若 $d_x>0$,说明上一个被填充的像素为 $(x,y_{x-1}+1)$,$d_x$计算为 $(x,y_{x-1}+0.5)$ 到目标直线的竖直距离。而 $d_{x+1}$ 计算为 $(x+1,y_{x}+0.5)$ 即 $(x+1,y_{x-1}+1.5)$ 到目标直线的竖直距离
\[d_{x+1}=d_x+k-1=d_x+\frac{y_2-y_1}{x_2-x_1}-1\]由算得的 $d_{x+1}$ 即可选择像素填充。
在上图中,由 $d_1$ 到 $d_2$、由 $d_2$ 到 $d_3$ 满足第一个递推式,而由 $d_3$ 到 $d_4$ 满足第二个递推式,即
\[\begin{gather} d_3>0\\ d_3'=-(1-d_3)=d_3-1\\ d_4=d_3'+k=d_3+k-1 \end{gather}\]第二个递推式也可像这样分部理解。
可是这种形式的递推式有浮点数除法 $\frac{y_2-y_1}{x_2-x_1}$ 的参与,而浮点数除法是比较慢的。为避免浮点数除法运算,令 $x_2-x_1=\Delta x,y_2-y_1=\Delta y$,这里 $x_2>x_1,y_2\ge y_1$(因为斜率 $0$ 到 $1$),在递推式两边同乘 $\Delta x$ ,则有
\[\Delta xd_{x+1}=\left\{\begin{split} &\Delta xd_x+\Delta y&d_x\le 0\\ &\Delta xd_x+\Delta y-\Delta x\quad&d_x>0\\ \end{split}\right.\]此式仅含浮点数乘法。
还能继续化简吗?
可以的。若限制 $x_1,y_1;x_2,y_2$ 都为整数,在此限制条件下
\[\begin{gather}\Delta x,\Delta y\in\mathbb{Z}\\ 2\Delta xd_{x_1}=2(y_1-(y_{x_1}+0.5))\Delta x=2(y_1-(y_1+0.5))\Delta x=-\Delta x\in\mathbb{Z} \end{gather}\]将递推式两边同乘 $2$
\[2\Delta xd_{x+1}=\left\{\begin{split} &2\Delta xd_x+2\Delta y&d_x\le 0\\ &2\Delta xd_x+2\Delta y-2\Delta x\quad&d_x>0\\ \end{split}\right.\]令 $f_x=2\Delta xd_x$,以之为判据,即
若 $f_{x+1}\le0$ 则填 $(x+1,y_x)$,若 $f_{x+1}>0$ 则填 $(x+1,y_x+1)$。
\[f_{x+1}=\left\{\begin{split} &f_x+2\Delta y&f_x\le 0\\ &f_x+2\Delta y-2\Delta x\quad&f_x>0\\ \end{split}\right.\]并且,若 $f_n\in\mathbb{Z}$,因为 $\Delta x,\Delta y\in\mathbb{Z}$,则 $f_{n+1}\in\mathbb{Z}$
又 $f_{x_1}=-\Delta x\in\mathbb{Z}$,由数学归纳法 $f_k,(k=x_1,x_1+1,\cdots,x_2)\in\mathbb{Z}$
于是最终的递推式只有整数运算,非常快速。
此算法便称为 Bresenham 画直线算法。
算法实现如下:
//Bresenham 直线算法
void BresenhamLine(int x1, int y1, int x2, int y2, Image& image)
{
int dx = abs(x1 - x2);
int dy = abs(y1 - y2);
int x = x1;
int y = y1;
int xStep, yStep, f;
Color color;
if (dy <= dx)
{
if (x2 < x1)
xStep = -1;
else
xStep = 1;
if (y2 < y1)
yStep = -1;
else
yStep = 1;
f = - dx;
image.setPixel(x, y, color.rgb(0, 0, 0));
while (x != x2)
{
x += xStep;
f += 2 * dy;
if (f > 0)
{
y += yStep;
f -= 2*dx;
}
image.setPixel(x, y, color.rgb(0, 0, 0));
}
}
else
{
if (x2 < x1)
xStep = -1;
else
xStep = 1;
if (y2 < y1)
yStep = -1;
else
yStep = 1;
f = - dy;
image.setPixel(x, y, color.rgb(0, 0, 0));
while (y != y2)
{
y += yStep;
f += 2 * dx;
if (f > 0)
{
x += xStep;
f -= 2*dy;
}
image.setPixel(x, y, color.rgb(0, 0, 0));
}
}
}
实现过程中,我将 f_x>0 情况下的递推式中 -2Δx 拆解到上个循环的末尾计算,可以少一次比较,提升速度。若全依照递推式,则算法为:
while (x != x2)
{
x += xStep;
if (f <= 0)
f += 2 * dy;
else
f += 2 * dy - 2 * dx;
if (f > 0)
y += yStep;
image.setPixel(x, y, color.rgb(0, 0, 0));
}
我绘制了一个样例图像来检验其效果:


可见其毛刺较为明显,图像不是很平滑,但是速度尤其快,耗时仅为:
Elapsed time: 0.026s
Bresenham 画圆算法

效果如图。与 Bresenham 画直线算法一致,画圆算法的思想仍是递推。将上图的局部放大得:
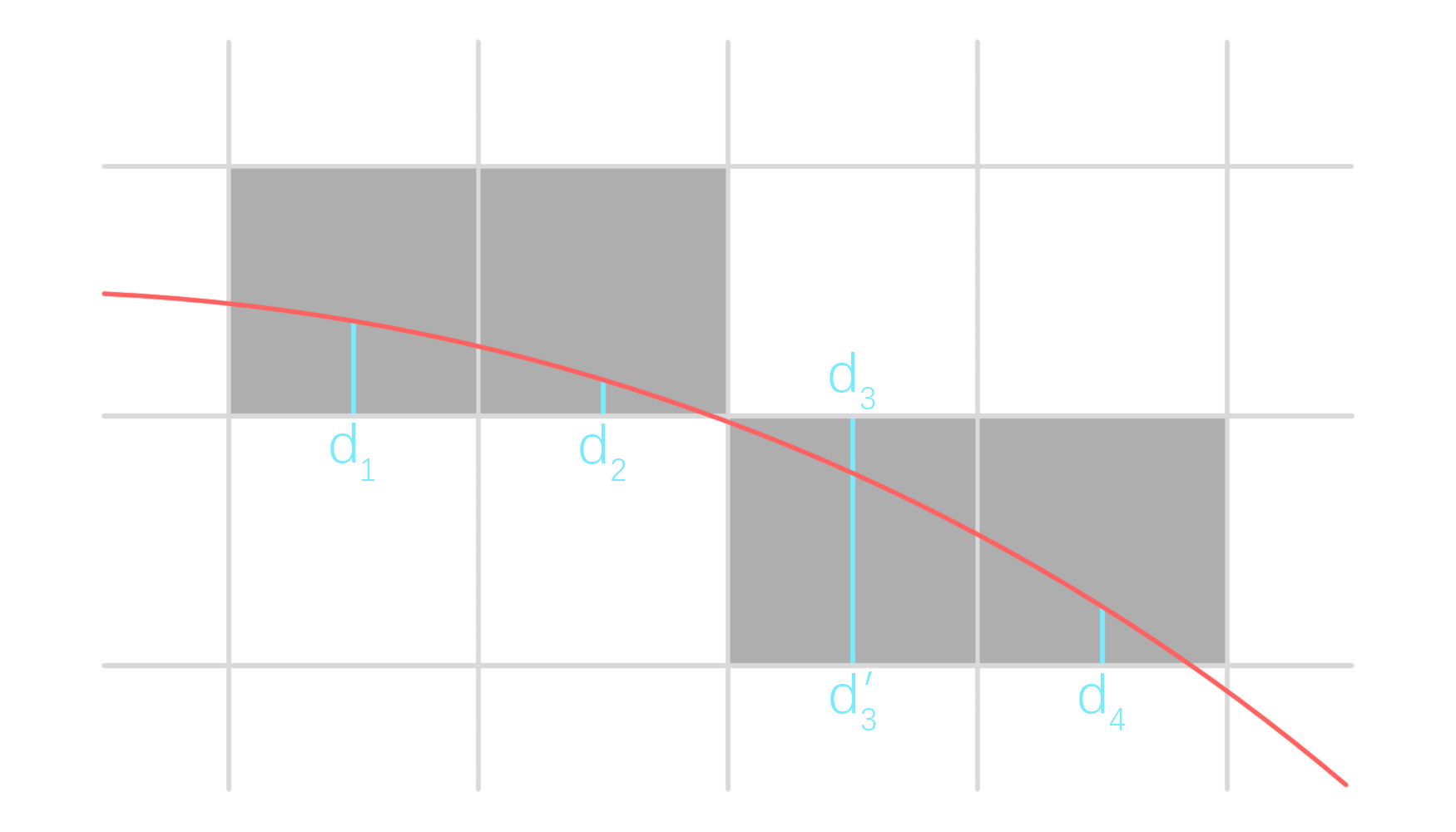
可以看出,被放大部分位于圆的上偏右 45° 区域。由圆被光栅化时的 8 等分对称性,我们只要绘制出上偏右 45° 区域,就能藉此画出整个圆。
一个圆由圆心 $(x_c,y_c)$ 与半径 $r$ 所表征,这里的 $x_c,y_c,r\in\mathbb{Z}$。
与 Bresenham 画直线算法类似,判据依然是待填充的两个像素的中点在目标圆弧之上还是目标圆弧之下,即竖直距离 $d$ 的正负。不过这里的两个待填充像素分别为 $(x+1,y_x)$ 和 $(x+1,y_x-1)$ ,两个像素的中点为 $(x+1,y_x-0.5)$ 。这种情况下
\[d_{x+1}=\sqrt{r^2-(x+1-x_c)^2}-(y_x-0.5-y_c)\]可见公式中含有程序员最讨厌的开方运算,耗时爆炸。不过有一个方法可以规避它:
定义
\[\delta_{x+1}=\left(\sqrt{r^2-(x+1-x_c)^2}\right)^2-(y_x-0.5-y_c)^2=r^2-(x+1-x_c)^2-(y_x-0.5-y_c)^2\]易知 $\delta$ 与 $d$ 的符号是一致的,故也可以作为判据。
下面计算递推式
\[\begin{split} \delta_{x+1}-\delta_x&=r^2-(x+1-x_c)^2-(y_x-0.5-y_c)^2-r^2+(x-x_c)^2+(y_{x-1}-0.5-y_c)^2\\ &=-2(x-x_c)-1-(y_x-0.5-y_c)^2+(y_{x-1}-0.5-y_c)^2 \end{split}\]若 $\delta_x\ge0$,$y_x=y_{x-1}$;若 $\delta_x<0$,$y_x=y_{x-1}-1$,故
\[\delta_{x+1}=\left\{\begin{split} &\delta_x-2(x-x_c)-1&\delta_x\ge0\\ &\delta_x-2(x-x_c)+2(y_x-y_c)-1\quad&\delta_x<0\\ \end{split}\right.\]考虑起始值 $\delta_{x_c}=r^2-(r-0.5)^2=r-0.25$
为规避浮点数,令 $x_r=(x-x_c),\ x_r=(y-y_c),\ f_{x_r}=4\delta_{x}$
所以
\[\begin{gather} f_0=4\delta_{x_c}=4r-1\\ f_{x_r+1}=\left\{\begin{split} &f_{x_r}-8x_r-4&\delta_x\ge0\\ &f_{x_r}-8x_r+8y_r-4\quad&\delta_x<0\\ \end{split}\right. \end{gather}\]得到了递推式,而且显然只包含整数计算!利用这个递推式与判据,即可绘制出上偏右45°圆弧,利用8等分对称性,就可以得到整个圆。
算法实现如下:
//Bresenham 画圆算法
void BresenhamCircle(int xc, int yc, int r, Image& image)
{
int xr = 0;
int yr = r;
int f = 4 * r - 1;
Color color;
image.setPixel(xc + r, yc, color.rgb(0, 0, 0));
image.setPixel(xc - r, yc, color.rgb(0, 0, 0));
image.setPixel(xc, yc + r, color.rgb(0, 0, 0));
image.setPixel(xc, yc - r, color.rgb(0, 0, 0));
while (xr <= yr)
{
f += -8 * xr - 4;
xr++;
if (f < 0)
{
f += 8 * yr;
yr--;
}
image.setPixel(xc + xr, yc + yr, color.rgb(0, 0, 0));
image.setPixel(xc + xr, yc - yr, color.rgb(0, 0, 0));
image.setPixel(xc - xr, yc + yr, color.rgb(0, 0, 0));
image.setPixel(xc - xr, yc - yr, color.rgb(0, 0, 0));
image.setPixel(xc + yr, yc + xr, color.rgb(0, 0, 0));
image.setPixel(xc + yr, yc - xr, color.rgb(0, 0, 0));
image.setPixel(xc - yr, yc + xr, color.rgb(0, 0, 0));
image.setPixel(xc - yr, yc - xr, color.rgb(0, 0, 0));
}
}
实现时与 Bresenham 画直线算法实现一样,将 y 变化时递推式的附加项放到上一个循环尾部计算来减少比较次数。
绘制样例图像以检验其效果:

与 Bresenham 画直线算法一样,其输出的图像其毛刺较为明显,不平滑,而且由于半径只能为整数,在绘制内部的圆时出现了间隔不降反增的现象,但输出速度快,耗时仅为:
Elapsed time: 0.033s
扫描线算法 (Scan-Line Filling)
顾名思义,扫描线算法的基本思想就是:用水平扫描线从上到下(或从下到上)扫描闭合图形,每根扫描线与图形的某些边产生一系列交点。交点有两类:穿入图形与穿出图形,且穿入图形交点之后必然跟着一个穿出图形交点。于是将这些交点按照 x 坐标排序,将排序后的点两两成对,作为线段的两个端点,这个线段必然在图形内部。以所填的颜色填充线段,多边形被扫描完毕后,颜色填充也就完成了。
扫描线算法绘制三角形示意:
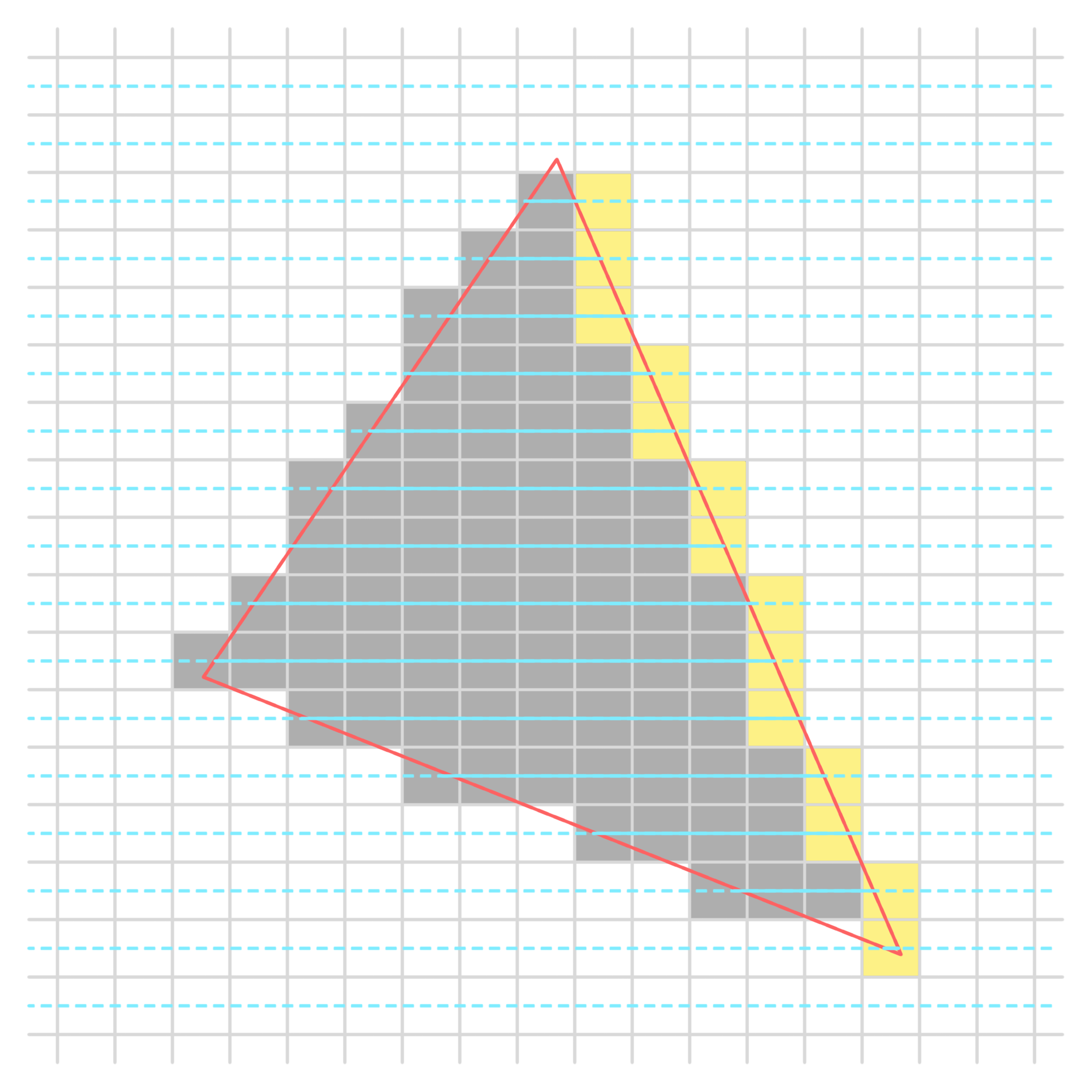
扫描线多边形填充算法
扫描线多边形填充算法是最常用的扫描线算法,尤其是三角形的扫描线填充算法。因为现在的 3D 模型大都以三角形作为面元,渲染器绘制模型时是基于面元绘制的,自然会大量使用三角形填充算法。
根据扫描线算法的基本思想,最容易想到的算法就是:
- 计算出扫描线能与多边形相交的范围;
- 对于每条扫描线算出其与多边形的交点;
- 按排序后交点,两两成对组成线段并填充;
如图:
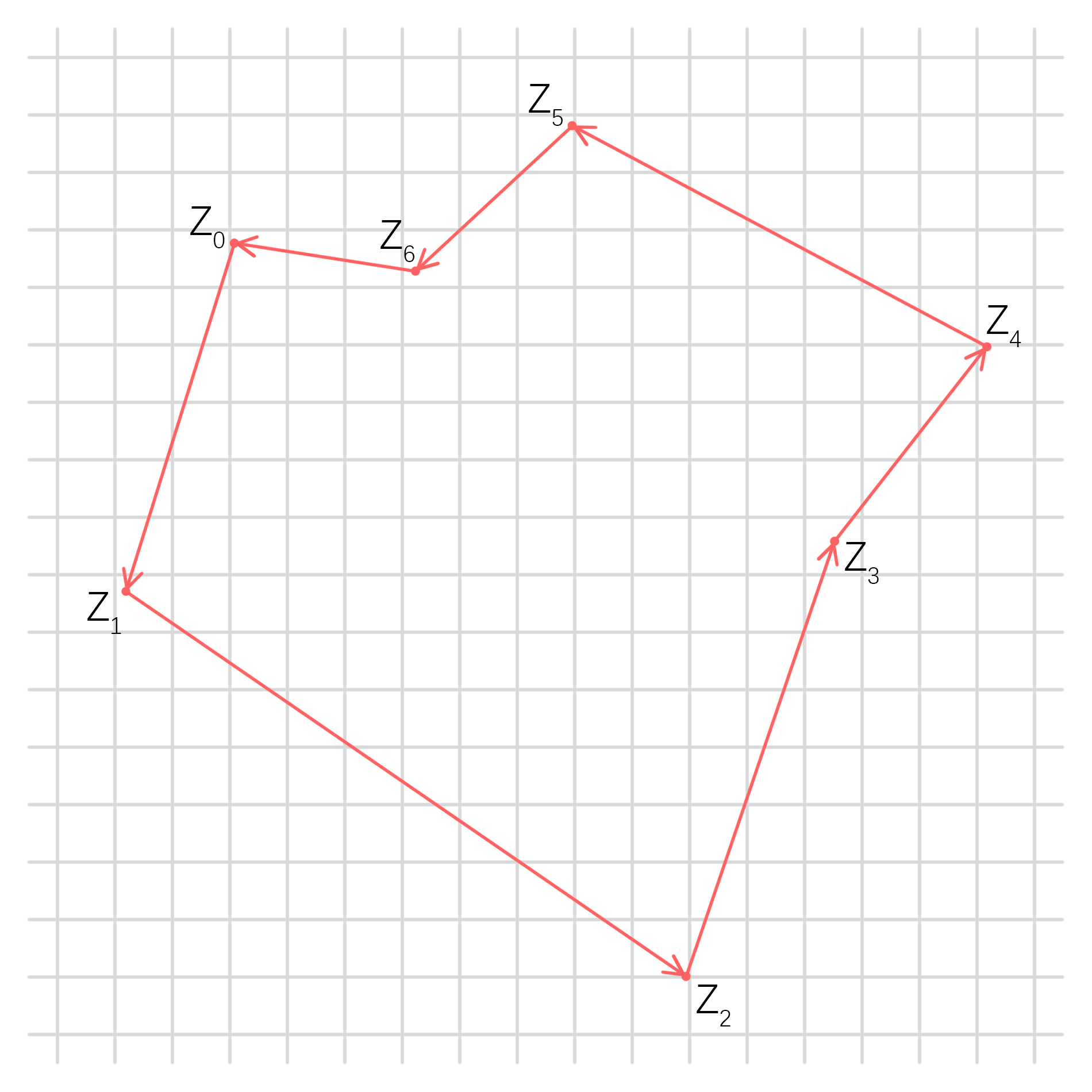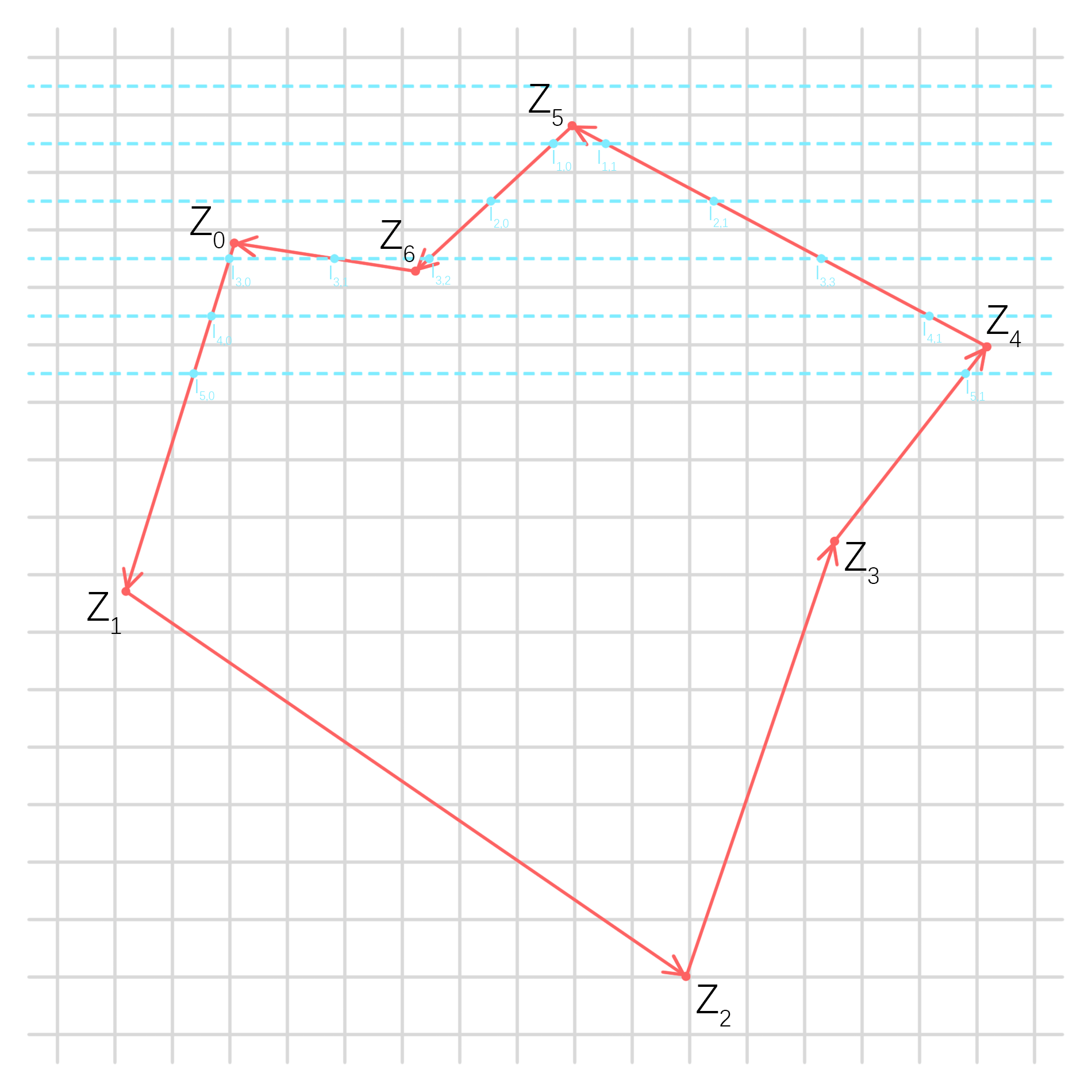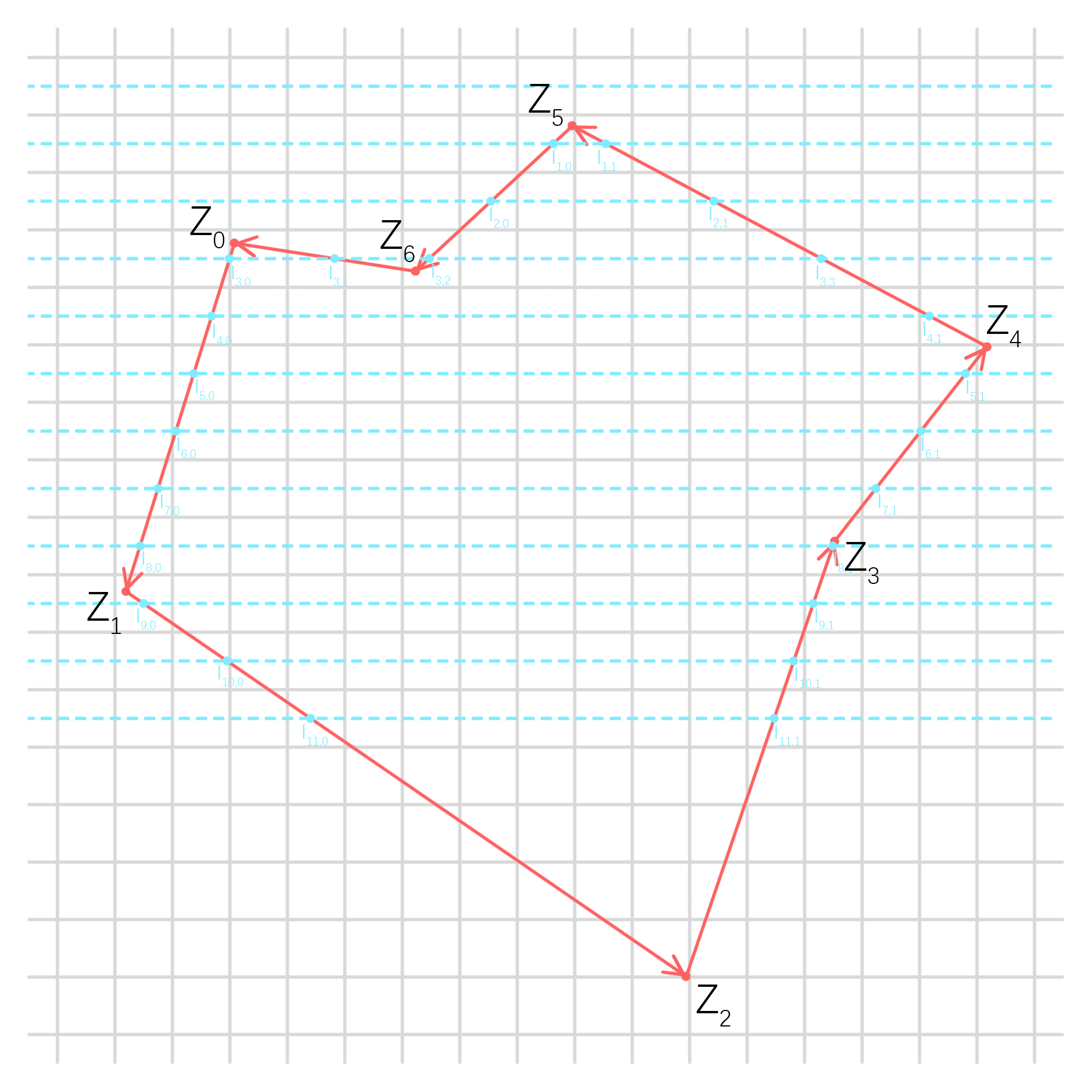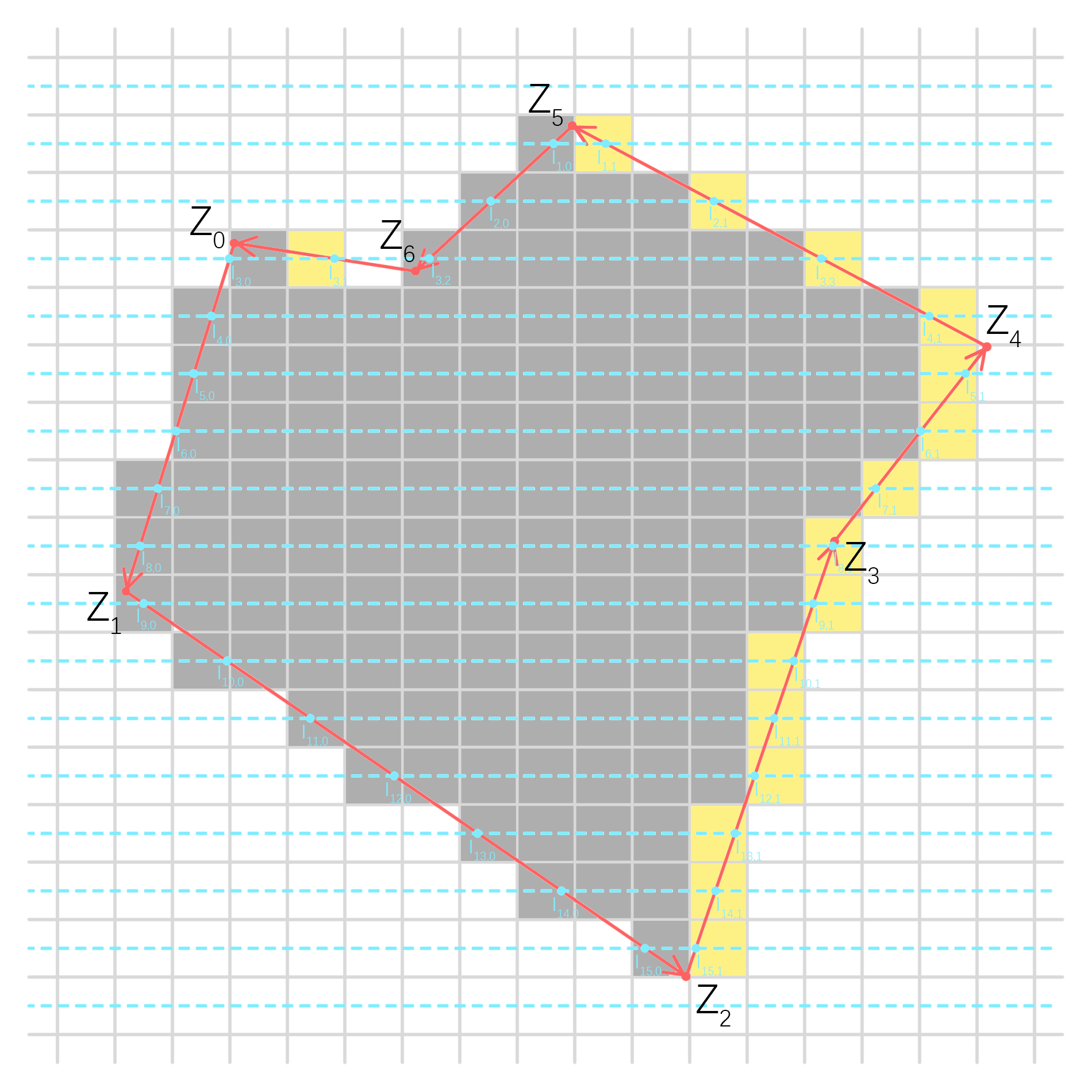
注意到扫描线穿出图形的交点是不填充的,这是为了处理一种很常见的情况:两个多边形共用一条边。此时,如果穿出点也填充,那么会导致一条边被两次填充的问题,这称为“左闭右开”准则。
这种朴素的算法虽然直观,但时间复杂度较高。对于每一条扫描线,都要对多边形的每一条边遍历求交点,含有大量的浮点数乘除法。而且多边形边的数据复杂度高于扫描线,应该减少对多边形边的重复计算。
更好的算法应该是:
- 计算出扫描线能与多边形相交的范围,生成一个表格来储存这些能相交的扫描线的交点;
- 对于多边形的每一条边,求出有几条扫描线与之相交,并求出这些扫描线对应的交点并填入存储交点的表格;
- 按排序后交点,两两成对组成线段并填充;
如图:
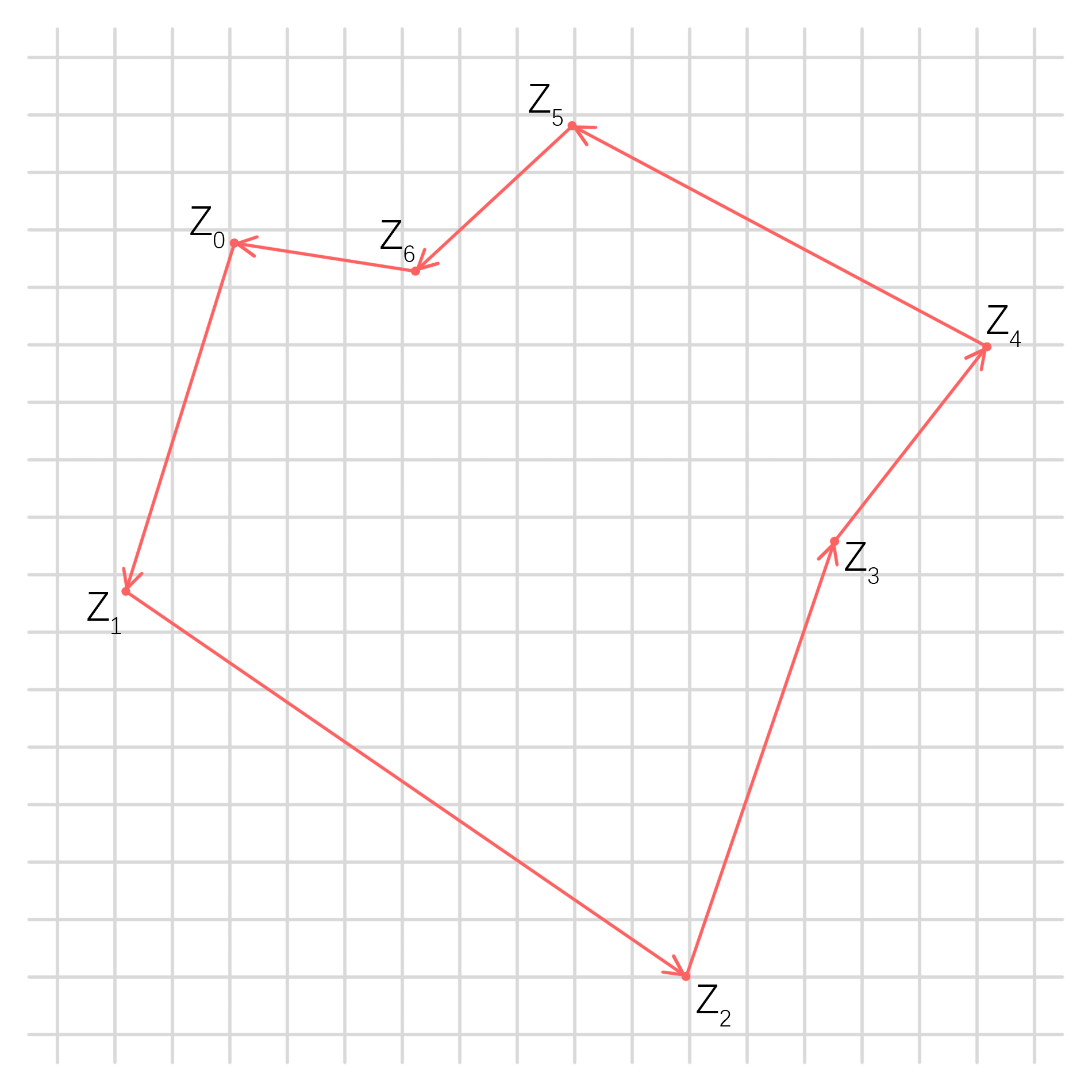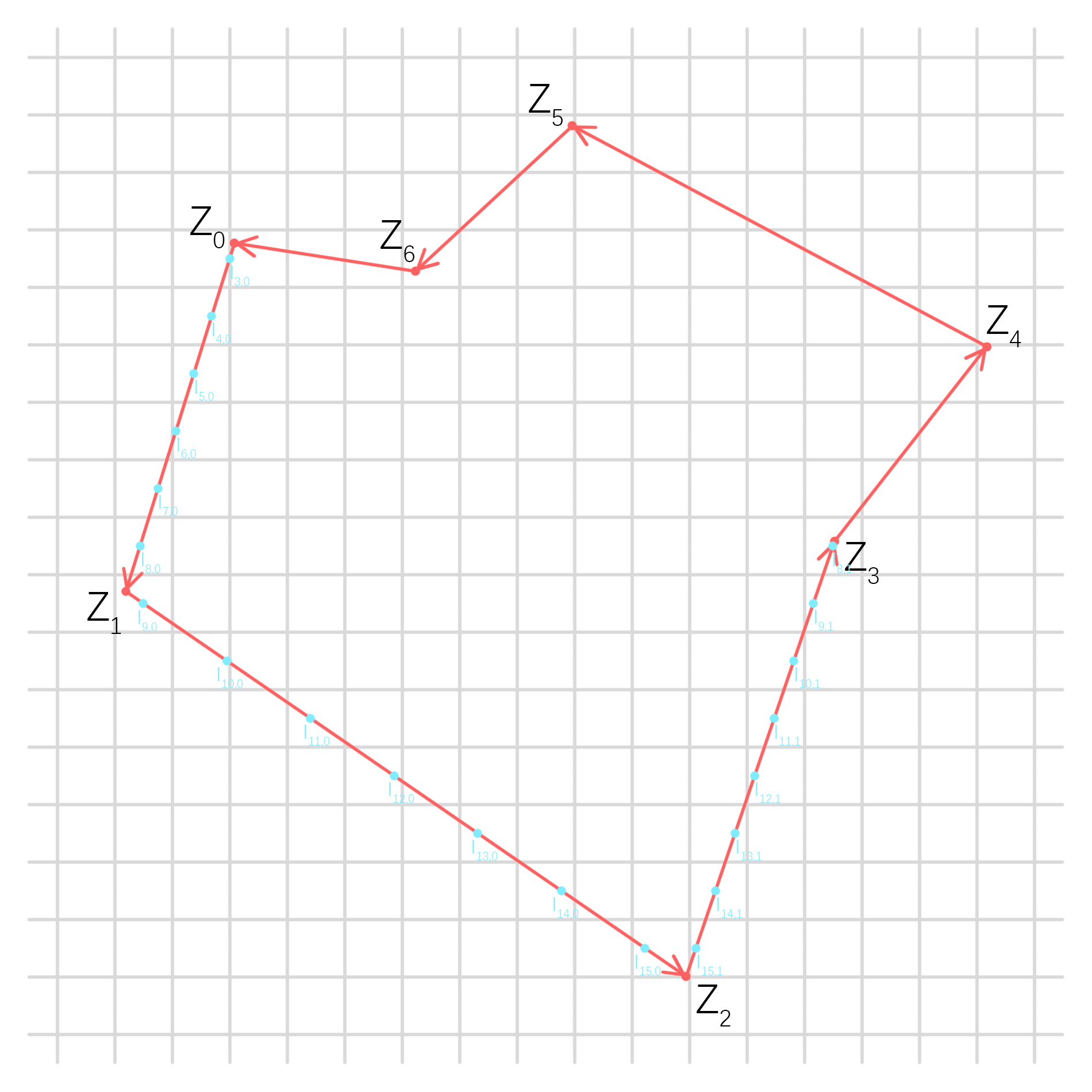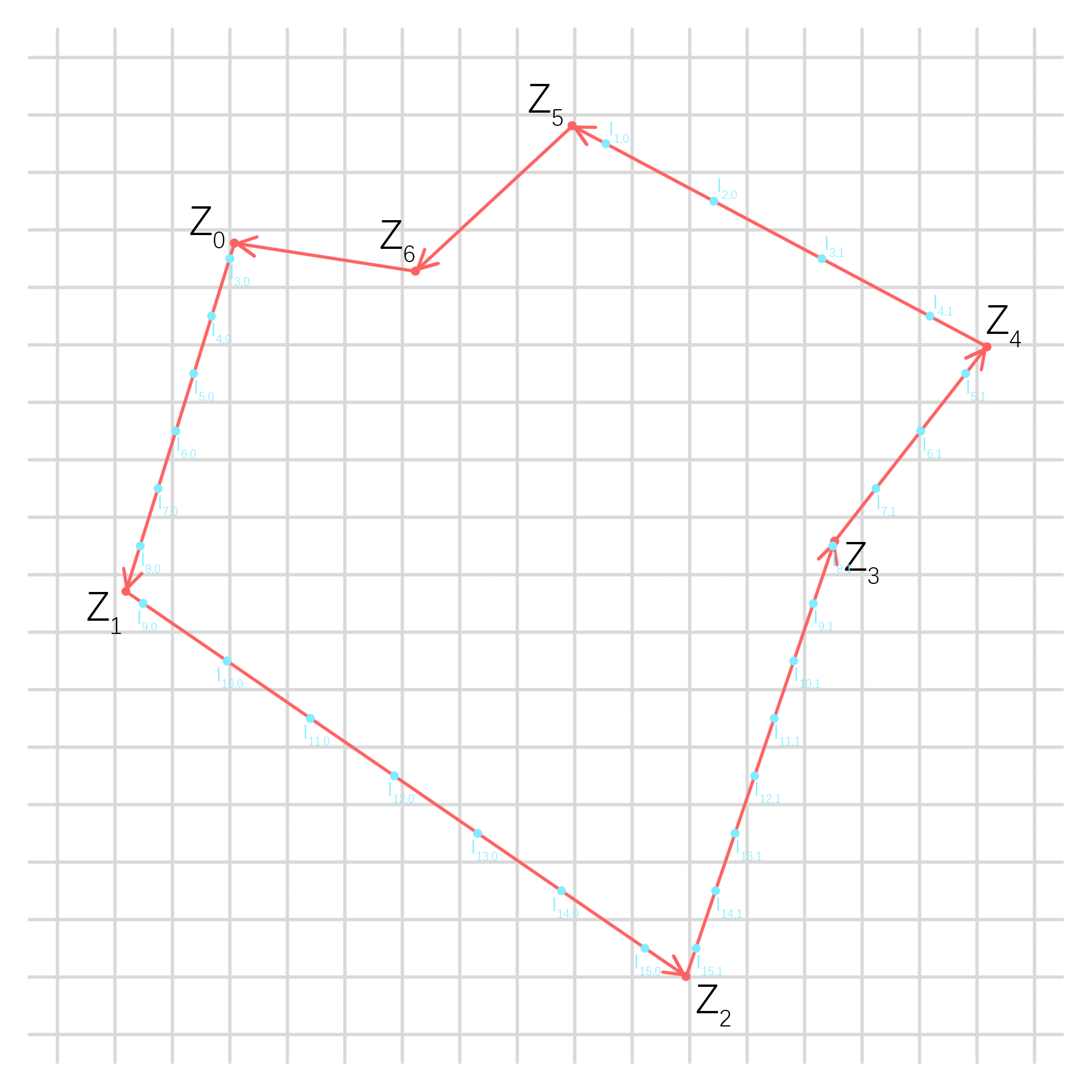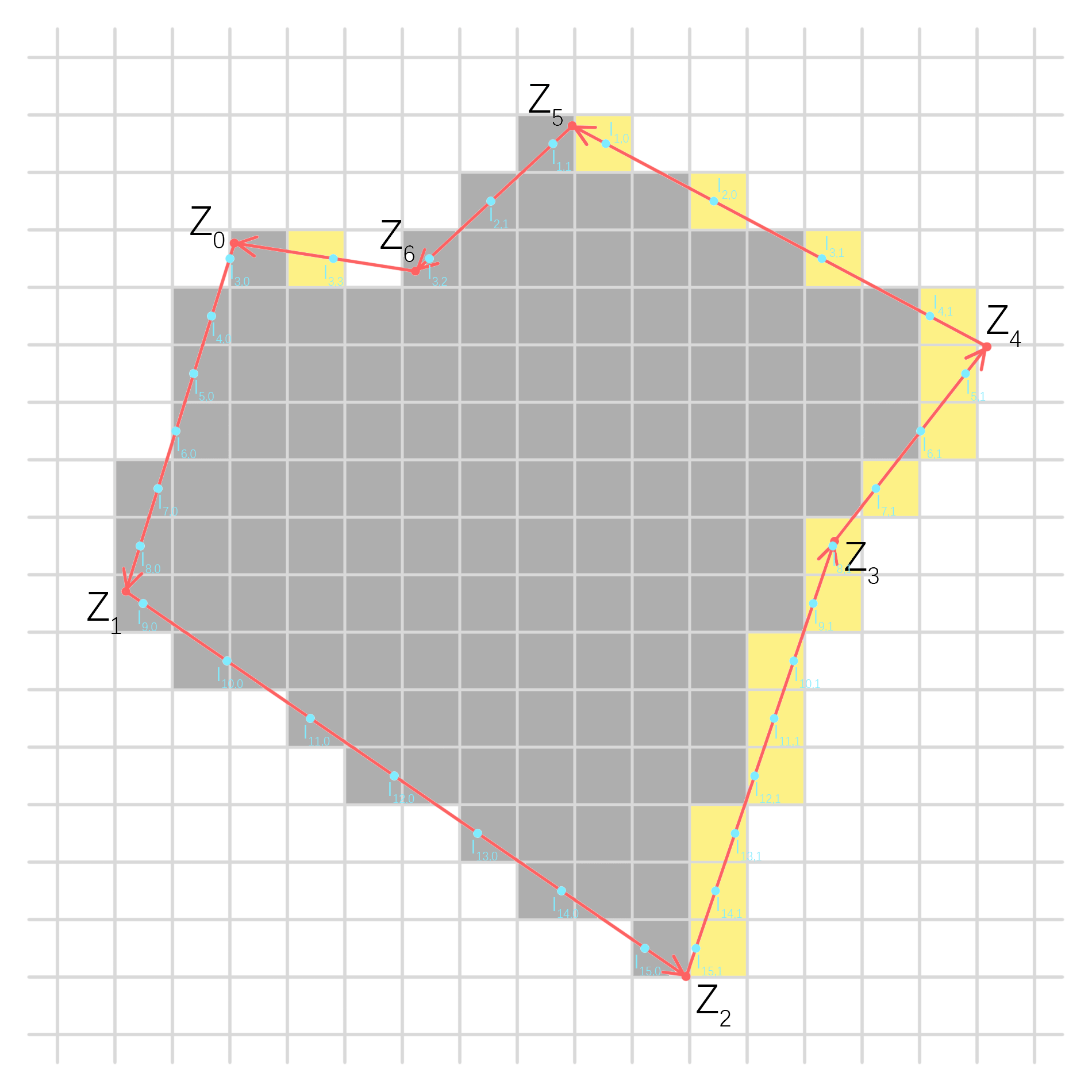
整个多边形由有向边表表示,围绕一圈形成一个环。
这种算法有一个显而易见的优势:在同一条边上的交点不用单独计算,而可以递推。我们只需求出最靠该边起点的第一个交点即可。
取其中一条边放大(右图):
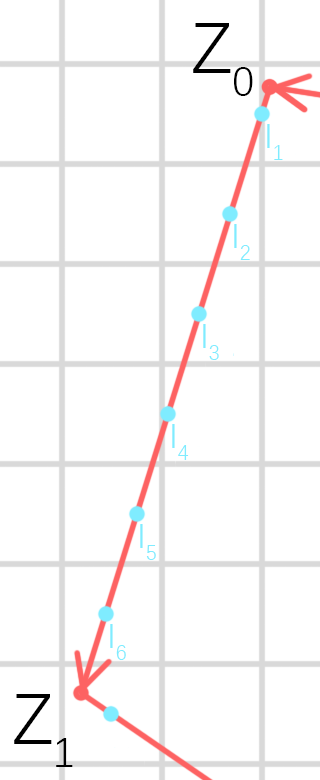
若边的起点的纵坐标比终点小,调换扫描顺序即可。
当然上面考虑的是一般情况,还有一些特殊情况要考虑:
1. 扫描线经过多边形顶点
这一点很重要,我们需要知道在这种情况下,应该有两个交点、一个交点还是没有交点?不然容易造成交点失配,导致这一整条扫描线的填色出错。试想在黑色色块中一道突兀的白线…
除了“左闭右开”准则,填充过程还需满足另外一个“上闭下开”准则。即:对于每一条边,起点和终点中纵坐标较高的点包含于这条边,而纵坐标较低的不包含于此边。这样一来,若扫描线经过纵坐标较高的端点,则这是一个交点;若扫描线经过纵坐标较低的端点,则这不是一个交点。
扫描线经过多边形顶点有三种情况:
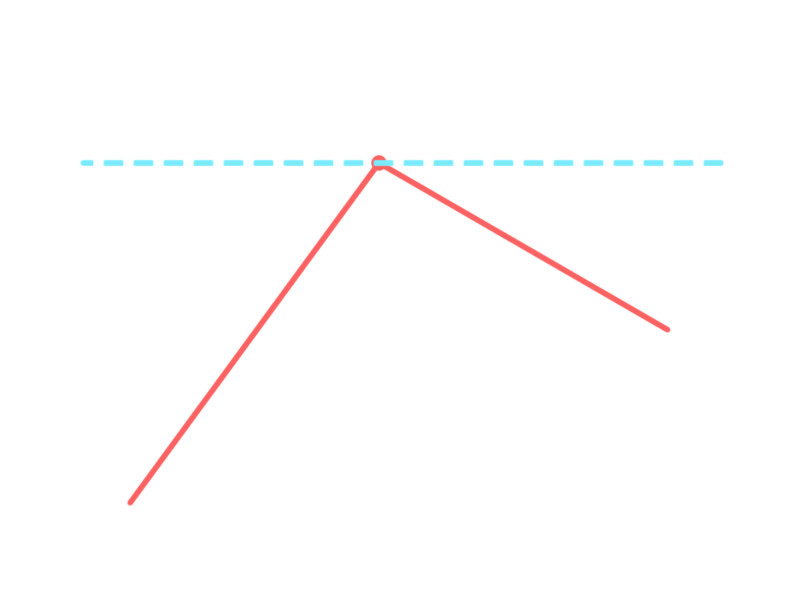
两条边都在扫描线下侧:
则两条边都认为相交,得到两个横坐标相同的交点。再由“左闭右开”准则,该点不会填色。
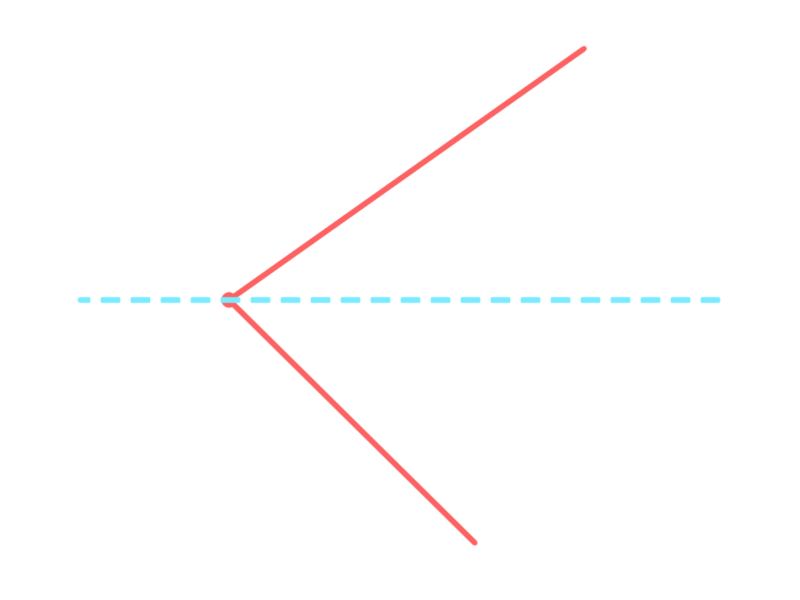
两条边分别位于扫描线两侧:
其中位于下侧的边认为相交,位于上侧的边认为不相交,得一个交点。
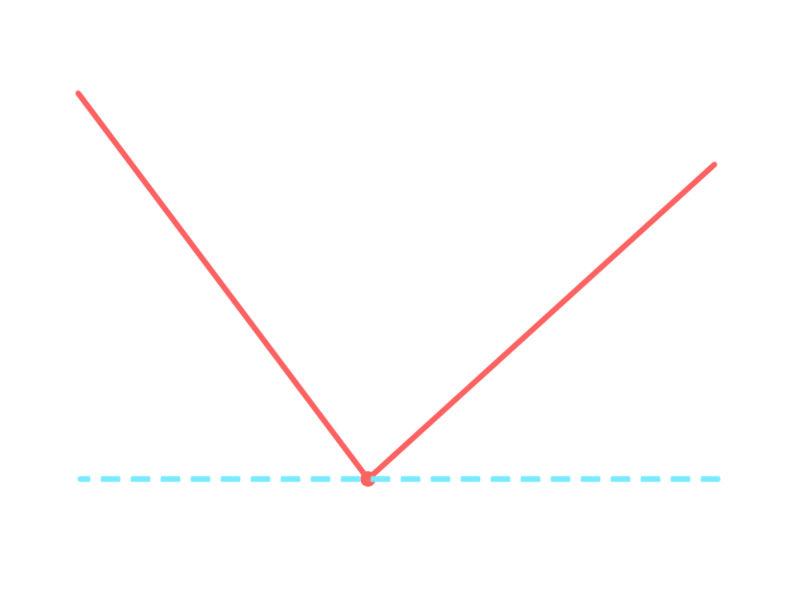
两条边都在扫描线上侧:
则两条边都认为不相交,不得到交点,该点不会填色。
可见有效解决扫描线经过多边形顶点时交点判断的问题。
2. 水平边如何处理
水平的边不参与求交点,直接省略即可。
接下来讨论一下算法所需的数据结构。
整个多边形由有向边表表示,对应数据结构要表示出每个顶点的坐标和顶点的逻辑联系(序偶)。
可用的数据结构有数组和循环单链表:
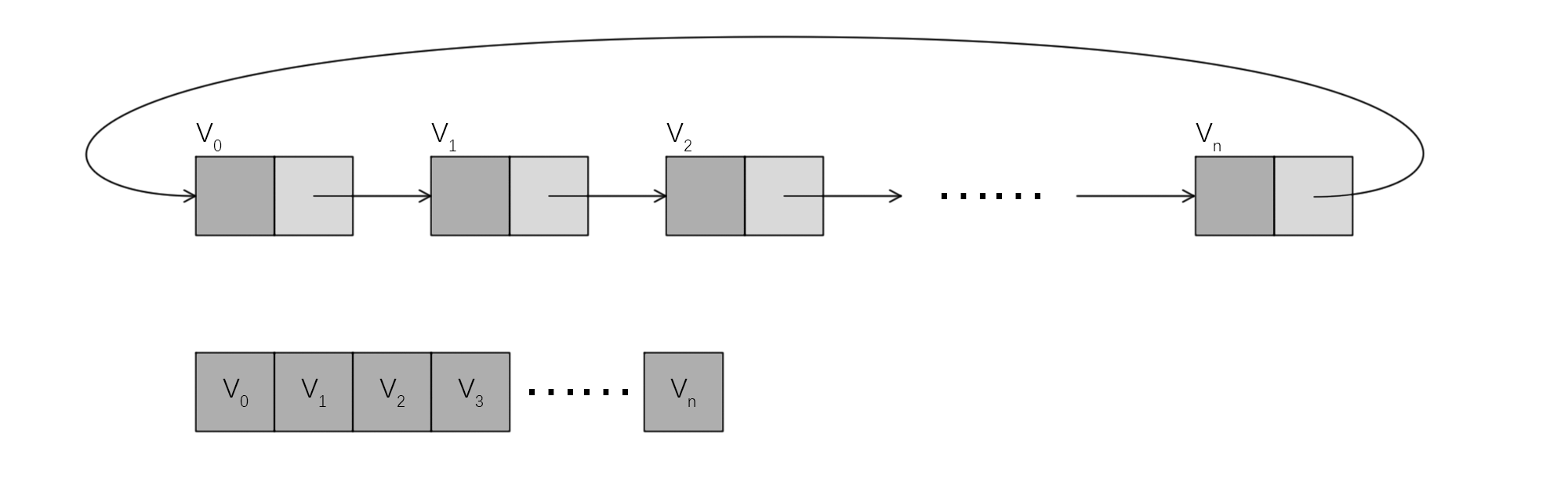
如果多边形是一次生成的,在初始化之后不会再加入顶点了,那么使用数组比较好。倒不是因为它具有随机访问的性质(因为本算法用不到随机访问,是顺序遍历各边的),而是因为它创建方便。如果多边形创建后还要插入顶点,可以使用循环单链表,链表具有较好的插入和拓展性质。
而对于用来保存每一条扫描线的交点的交点表,由于此表是在遍历有向边表的过程中不断插入排序生成的,使用插入与拓展性质优越的链表相较于数组更有优势。而且可能相交的扫描线条数是已知的,即为顶点中最大纵坐标的向下取整减去最小纵坐标的向上取整,考虑到“上闭下开”准则,若最小纵坐标为整值,还应减 1。这样一来,链表条数固定,一个链表数组应该是最优的选择:
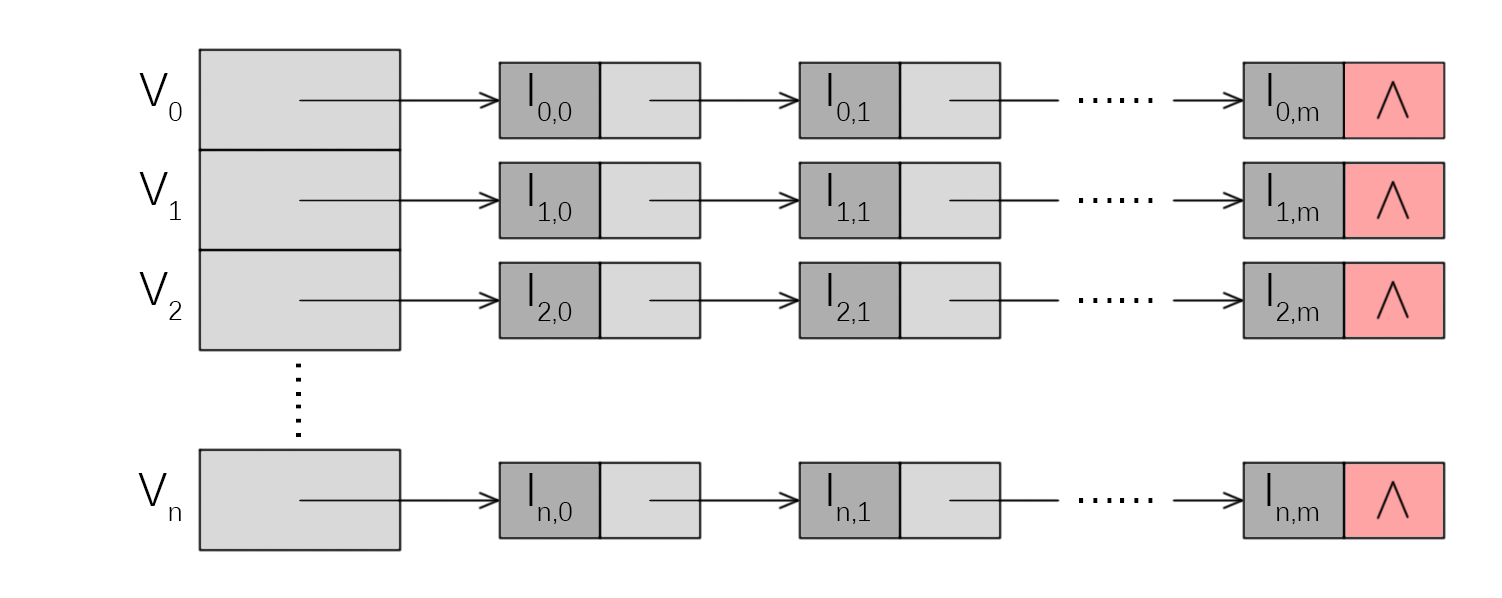
算法实现如下。
先编写一个工具类:向量(Vector),并定义其运算
// 二维向量,比较易懂,就不注释了
class Vector {
public:
double x;
double y;
Vector() { x = 0; y = 0; }
Vector(double x, double y) { this->x = x; this->y = y; }
Vector(const Vector& V) { x = V.x; y = V.y; }
~Vector() {}
Vector& operator=(const Vector& V) { x = V.x; y = V.y; return *this; }
Vector operator-() { return Vector(-x, -y); }
Vector operator+(const Vector& V) { return Vector(x + V.x, y + V.y); }
Vector operator-(const Vector& V) { return Vector(x - V.x, y - V.y); }
double operator*(const Vector& V) { return x * V.x + y * V.y; }
Vector operator*(double k) { return Vector(x * k, y * k); }
double module() { return sqrt(x * x + y * y); }
Vector unitVector() { return *this * (1.0 / module()); }
Vector normalVector() { return Vector(-y, x).unitVector(); }
};
接着完成扫描线多边形填充算法
// 扫描线多边形填充算法
void scanLinePolygon(std::initializer_list<Vector> vertexes, Image& image) {
// initializer_list 是 C++11 的新特性,本质上就是一个能表示其长度的数组
// 它有 3 个成员函数:size()、begin() 和 end(),意义与一般数组一致
Color color;
// 交点链表类型定义
typedef struct intersection {
double x;
struct intersection* next;
} intersection;
// ... 代码省略(保持与原文一致)
}
绘制一个五角星试试:


扫描线直线填充算法
此算法即为上文多边形填充算法的特例,根据直线端点与宽度计算出对应矩形即可。
// 扫描线直线填充算法
void scanLineLine(Vector E1, Vector E2, double width, Image& image) {
scanLinePolygon({
E1 + (E2 - E1).normalVector() * (width / 2),
E2 + (E2 - E1).normalVector() * (width / 2),
E2 - (E2 - E1).normalVector() * (width / 2),
E1 - (E2 - E1).normalVector() * (width / 2)}, image);
}
绘图样例:


可见由于支持绘制不同宽度的直线,图像立体感更强了。
绘制过程也非常迅速:
Elapsed time: 0.036s
扫描线圆填充算法
用扫描线填充圆会造成畸形的问题,对越小的圆越严重(如下图),所以就不再使用了:

有符号距离场算法 (SDF)
有符号距离场,即 Signed Distance Field,缩写 SDF。也有称之为符号距离函数的,下面是 百度百科 对符号距离函数的定义:
符号距离函数(sign distance function),简称 SDF,又可以称为定向距离函数(oriented distance function),在空间中的一个有限区域上确定一个点到区域边界的距离并同时对距离的符号进行定义:点在区域边界内部为正,外部为负,位于边界上时为 0。
不过我更愿意将它定义为内部为负,外部为正,问题不大。
例如一个圆的 SDF,我们用颜色使它可视化:红色代表距离为负,蓝色代表距离为正,颜色的深度代表距离的长短。那么它长这样:

很显然白色的那一圈就是圆周的位置。
因为是“距离”的标量场,所以用“距离”保留了空间信息,这些额外的信息能够在进行一些其他算法,如光线步进(光线追踪的一种)时带来方便。
这个算法也很简单,在得到了 SDF 之后,只要对每个像素的位置计算距离值,为负填色,为正不填即可。所以说,关键在于怎样得到或计算 SDF。
圆的有符号距离场
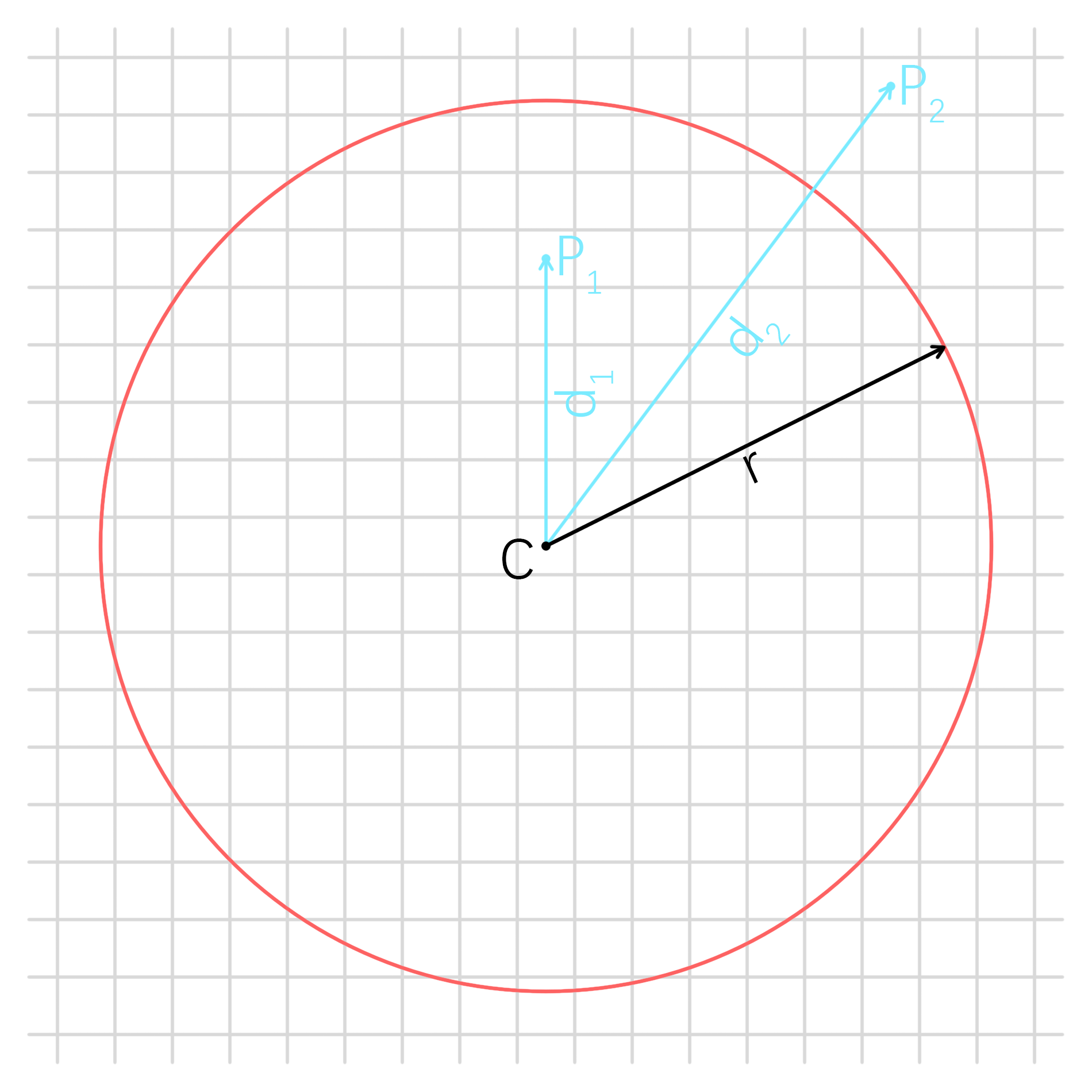
圆的 SDF 非常简单,即为目标点到圆心的距离减去半径:
\[f_{Circle}(\boldsymbol P)=d(\boldsymbol P,\boldsymbol C)-r\]而圆环呢?也很容易就能想到,对于圆环来说,圆的内部就是它的外部,它的 SDF 就是对应圆的 SDF 取绝对值,考虑上圆环的宽度,应为:
\[f_{Ring}(\boldsymbol P)=\|d(\boldsymbol P,\boldsymbol C)-r\|-\frac w2\]在这里我们实现一下圆环的 SDF 填充算法:
//有符号距离场圆环填充算法
void SDFRing(Vector C, double r, double w, Image& image)
{
Color color;
Vector P;
//不用遍历整个画布,只要遍历可能被填充的像素
for (P.x = floor(C.x - r - w); P.x <= ceil(C.x + r + w); P.x++)
for (P.y = floor(C.y - r - w); P.y <= ceil(C.y + r + w); P.y++)
if (fabs((C - P).module() - r) - (w / 2) <= 0)
image.setPixel(P.x, P.y, color.rgb(0, 0, 0));
}
效果:
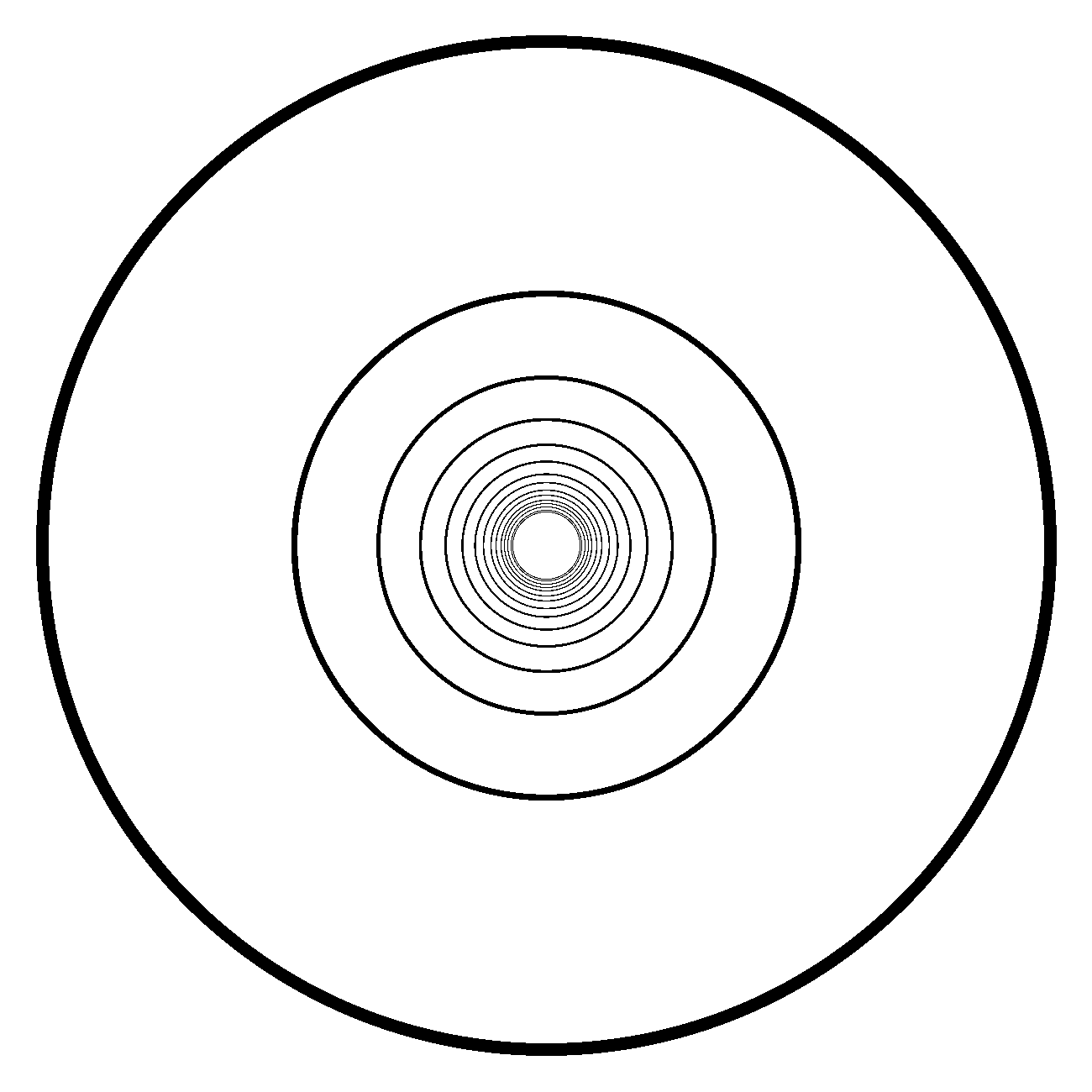

可见圆环也拥有了宽度,但由于此算法需要对每个像素计算,耗时较长:
Elapsed time: 0.198s
直线(胶囊)的有符号距离场
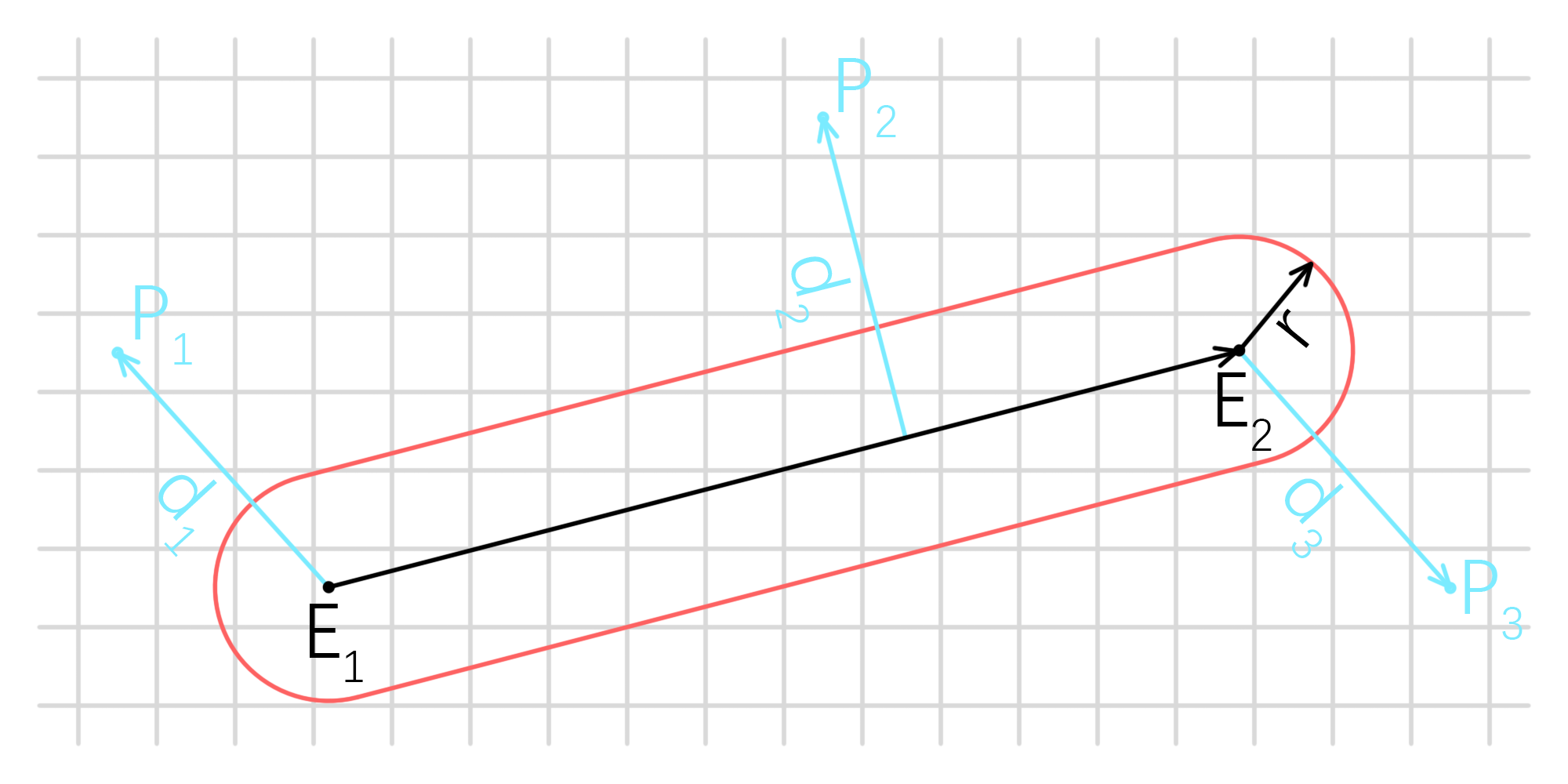
胶囊指的就是上图中红线围成的形状像 💊 的东东,这里我们用它来绘制直线。
这玩意儿的 SDF 需要分成三段讨论:
\[f_{Capsule}(\boldsymbol P)=\left\{\begin{split} &d(\boldsymbol P,\boldsymbol E_1)&(\boldsymbol P-\boldsymbol E_1)\cdot(\boldsymbol E_2-\boldsymbol E_1)\le0\\ &d(\boldsymbol P,\boldsymbol E_2)&(\boldsymbol P-\boldsymbol E_2)\cdot(\boldsymbol E_2-\boldsymbol E_1)\ge0&\\ &d(\boldsymbol P,\boldsymbol{E_1E_2})\quad\quad&otherwise \end{split}\right.\]也很容易理解。
算法实现:
//有符号距离场直线填充算法
void SDFLine(Vector E1, Vector E2, double w, Image& image)
{
Color color;
Vector P, t1, t2;
int f; //SDF值
//计算可能被填充的像素范围
int xl = floor(min(E1.x, E2.x) - w / 2);
int xh = ceil(max(E1.x, E2.x) + w / 2);
int yl = floor(min(E1.y, E2.y) - w / 2);
int yh = ceil(max(E1.y, E2.y) + w / 2);
//不用遍历整个画布,只要遍历可能被填充的像素
for (P.x = xl; P.x <= xh; P.x++)
for (P.y = yl; P.y <= yh; P.y++)
{
t1 = E2 - E1;
t2 = P - E1;
if (t1 * t2 <= 0)
f = t2.module() - w / 2;
else if ((t2 = P - E2) * t1 >= 0)
f = t2.module() - w / 2;
else
f = fabs(t1.normalVector() * t2) - w / 2;
if (f <= 0)
image.setPixel(P.x, P.y, color.rgb(0, 0, 0));
}
}
同样绘制一下测试样例:


运算时间较长,可以接受:
Elapsed time: 0.328s
代码
本节代码请查看:🔗 Github: JeffreyXiang/DrawWithCpp
总结
本文介绍了三种常见的绘图算法,分别是:
- Bresenham 算法
- 扫描线算法 (Scan-Line Filling)
- 有符号距离场算法 (SDF)
其中 Bresenham 算法与扫描线算法是非常经典的计算机图形学算法,它们的优点很明显:速度快、效率高。但缺点同样明显:不含任何空间信息,难以进行光线追踪、碰撞检测等进阶算法;只能以直线储存表面,容易造成锯齿。而有符号距离场算法尽管速度较慢,但能保留大量空间信息,且能绘制弧线(三维则为球面)。
我们的目的是一个画图程序,并不是实时渲染。对时间复杂度的要求不高,而希望图像尽可能精细。因此,我们的程序将使用 SDF 算法。
预告
下文我们将用面向对象的方法改写之前的 SDF 代码,并定义更多图形及其 SDF。
