Jianfeng Xiang | Blogs | 用 Taichi 学光线追踪（三）：光照进阶

序言

在完成了 BVH 加速结构、三角网格与材质系统之后，我们的渲染器终于能够处理复杂的几何场景，并把 glTF 模型渲染到屏幕上。虽然这已初步具备了通用渲染器的雏形，但画面效果依旧显得“生硬”：金属缺乏细腻的高光，粗糙表面显得不够自然，光线的传播也仍停留在最基础的随机反弹。

如果说第二篇为渲染器搭起了骨架与外壳，那么这一篇则是为它注入血肉与灵魂。我们将真正迈向物理正确的光传输：以渲染方程和蒙特卡洛积分为理论基石，引入更真实的材质模型（如 GGX 微平面分布），并借助直接光源采样、多重重要性采样以及环境光重要性采样，让路径跟踪在有限的计算预算下依然能够高效收敛。

在这里，渲染器将迎来一次质变：不再依赖粗糙的近似，而是从第一性原理出发，在保证物理正确性的同时追求视觉的真实，并在数学方法的加持下兼顾计算效率，逐步逼近现代光线追踪的核心。

19. 渲染方程与蒙特卡罗方法

代码：GitHub

在前面的实现中，我们的路径跟踪踪器采用了一种非常“经验化”的做法：每次相交后根据材质属性随机采样一个弹射方向，然后继续递归追踪。虽然这种方式能得到图像，但它隐含地假设所有采样贡献相同，没有考虑传输函数与采样概率在能量传输中的作用。结果就是，画面看似合理，却缺乏严格的物理意义。

要让渲染器真正具备“物理正确性”，我们需要从第一性原理出发，建立描述光能量传输的方程，并用合适的数值方法去近似解它。这就是渲染方程（Rendering Equation）与蒙特卡罗方法（Monte Carlo Integration）的由来。

19.1 辐射度量学

在进入渲染方程之前，我们需要先回答一个更基础的问题：渲染的物理本质是什么？

渲染的目标是生成一张“看起来真实”的图像。而所谓“真实”，在物理层面上就是对光与物体相互作用后进入成像设备（如人眼或相机）的过程的模拟。换句话说，一幅图像的形成，本质上是场景中物体与光源交互后，经过几何光学传播最终抵达观察者的结果。

因此，要想让渲染具备物理一致性，就必须建立在光的物理量度之上，而这一套描述和度量光能量的理论体系便是辐射度量学（Radiometry）。

辐射度量学的核心目标，是回答这样几个问题：

光有多少？ —— 用能量的形式进行度量。
光如何传播？ —— 描述方向性分布。
光与物体相互作用？ —— 描述物体的反射、折射、吸收等行为。
光如何被感知？ —— 解释相机或人眼如何将光转化为图像信号。

在继续了解辐射度量学之前，我们可以先建立一个简单的类比：把光子想象成源源不断喷射出来的小球。它们在空间中飞行、碰撞、被吸收或反射，而辐射度量学中的各种物理量，正是用来描述这些小球在时间和空间上的分布与流动方式。

下面我们依次来看几个最常用的基本物理量。

插图来源：GAMES101: 现代计算机图形学入门

辐射能（Radiant Energy, $Q$）

辐射能是最直观的量：它直接描述光所携带的能量本身。

单位：焦耳 ($\text{J}$)
符号：$Q$

\[Q\ [\text{J}]\]

如果你把光看成无数小球（光子）在飞行，那么辐射能就是这些小球的“总能量”。

辐射通量（Radiant Flux, $\Phi$）

在物理上，我们往往更关心能量随时间的流动速率。这就是辐射通量：

定义：单位时间内穿过某个区域的辐射能量总和。
单位：瓦特 ($\text{W} = \text{J}/\text{s}$)

公式为：

\[\Phi = \frac{\text{d}Q}{\text{d}t}\ [\text{W}]\]

在渲染中，辐射通量是光源“能量总量”的度量。可以把它看作所有其他辐射量的“母量”，后续的各种定义（强度、亮度、照度）其实都是它在方向、面积和角度上的细化。

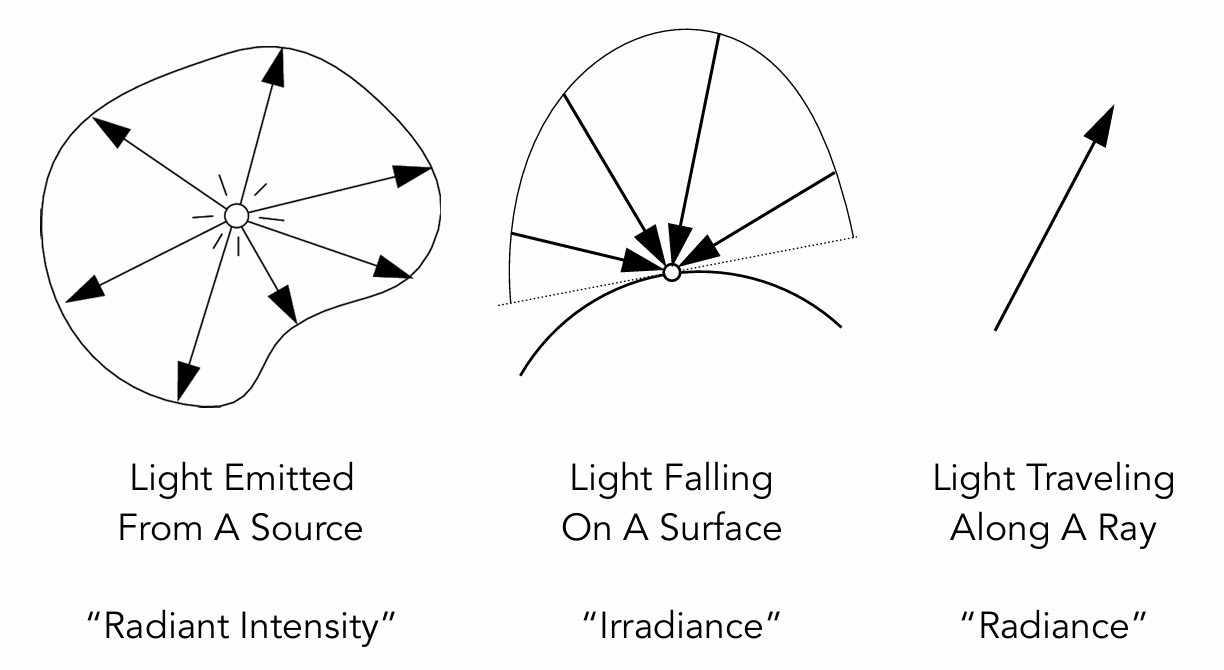
辐射强度（Radiant Intensity, $I$）

辐射强度描述的是：光源在某个方向上释放了多少能量。

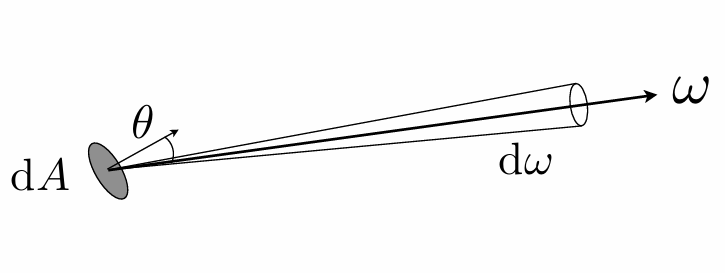
定义：单位立体角上的辐射通量
单位：瓦特每球面度 ($\text{W}/\text{sr}$)

公式为：

\[I(\boldsymbol{\omega}) = \frac{\text{d}\Phi}{\text{d}\boldsymbol{\omega}}\ \left[\frac{\text{W}}{\text{sr}}\right]\]

对各向同性点光源（各个方向都一样）来说：

\[\Phi = \int_{\mathbb{S}^2} I\ \text{d}\boldsymbol{\omega} = 4\pi I, \quad I = \frac{\Phi}{4\pi}\]

辐照度（Irradiance, $E$）

如果说辐射强度是“光源发出的多少能量”，那么辐照度就是“一个表面接收了多少能量”。

定义：单位面积上接收到的辐射通量
单位：瓦特每平方米 ($\text{W}/\text{m}^2$)

公式为：

\[E(\boldsymbol{p}) = \frac{\text{d}\Phi(\boldsymbol{p})}{\text{d}A}\ \left[\frac{\text{W}}{\text{m}^2}\right]\]

关键影响因素：

光源距离 → 离得越远，能量分散越大
入射角度 → 倾斜角度越大，投影面积越大，单位面积得到的能量越少

后者用 Lambert 余弦定律描述：

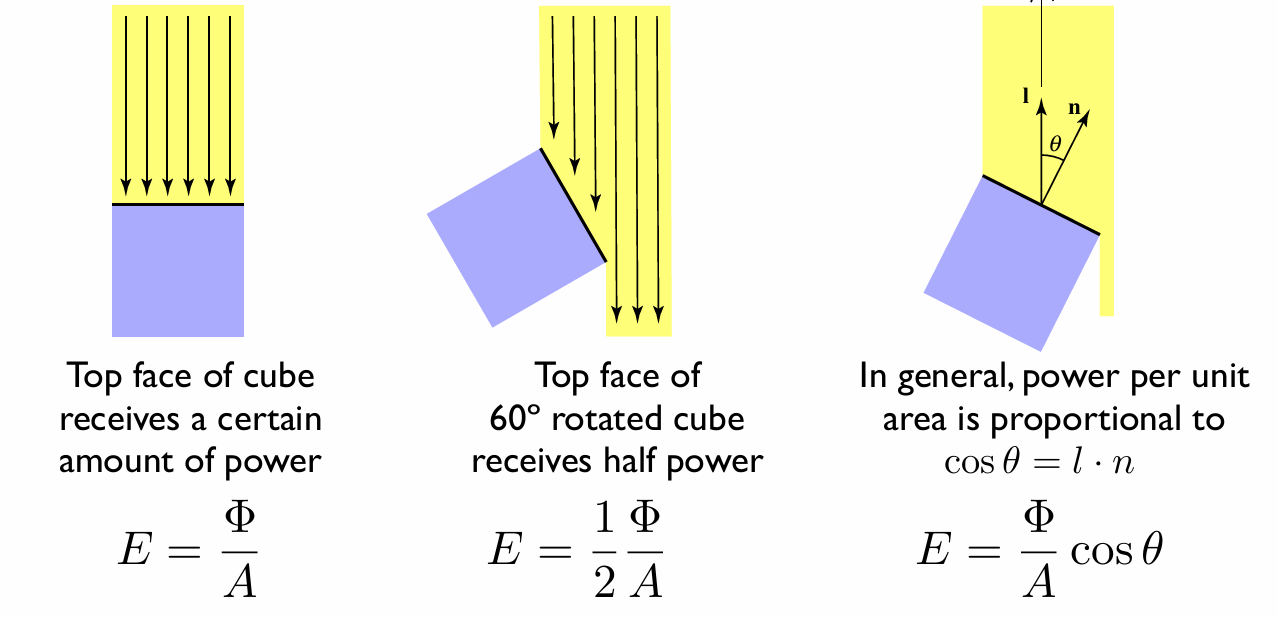
直观理解：一块表面对光“斜着摆”，看上去接住的光就更少。

辐亮度（Radiance, $L$）

最后，也是渲染中最核心的量——辐亮度。

定义：在某点、某方向上，光的通量密度。它是对辐射通量按 面积投影 和 立体角 的双重细分。
单位：瓦特每平方米每球面度 ($\text{W}/\text{m}^2 \cdot \text{sr}$)

公式为：

\[L(\boldsymbol{p}, \boldsymbol{\omega}) = \frac{\text{d}^2\Phi(\boldsymbol{p}, \boldsymbol{\omega})}{\text{d}A\cos\theta\ \text{d}\boldsymbol{\omega}}\ \left[\frac{\text{W}}{\text{m}^2\cdot sr}\right]\]

为什么辐亮度如此重要？

第一点：辐亮度是光传输过程中的守恒量，沿光线保持恒定。

可以直观证明如下：

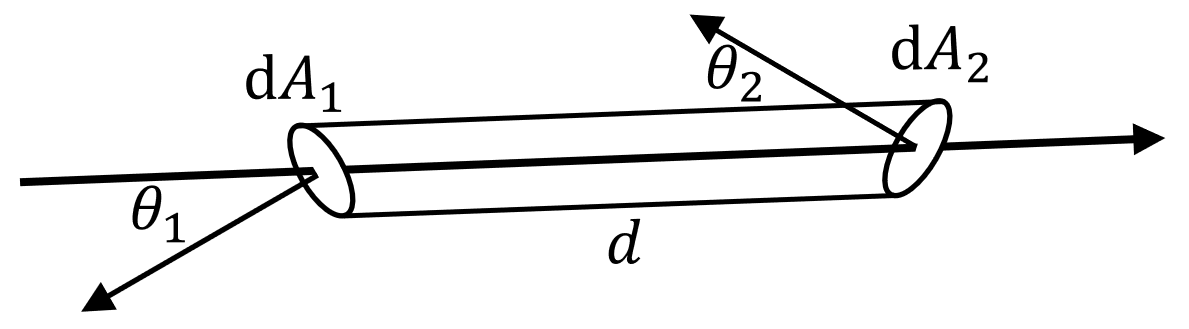
如图所示，空间中有两个面积微元 $\text{d} A_1,\ \text{d} A_2$，两个面积微元距离 $d$，与连线方向夹角分别为$\theta_1,\ \theta_2$ 。

考察通过这两个面积微元围成管道的光线（同时通过两个面积微元），则光线穿过微元 $\text{d} A_1$ 和 $\text{d} A_2$ 的通量分别为：

\[\Phi_1 = L_1\ \text{d} A_1\cos\theta_1 \text{d}\boldsymbol{\omega}_1 = L_1\ \text{d} A_1\cos\theta_1 \frac{\text{d}A_2\cos\theta_2}{d^2} = L_1\ \frac{\text{d}A_1\text{d}A_2\cos\theta_1\cos\theta_2}{d^2}\] \[\Phi_2 = L_2\ \text{d} A_2\cos\theta_2 \text{d}\boldsymbol{\omega}_2 = L_2\ \text{d} A_2\cos\theta_2 \frac{\text{d}A_1\cos\theta_1}{d^2} = L_2\ \frac{\text{d}A_1\text{d}A_2\cos\theta_1\cos\theta_2}{d^2}\]

因为光线穿过管道不会凭空消失或增加，这个两个通量应该相等，则：

\[L_1 = L_2\]

第二点：辐亮度决定了相机成像

如果说辐射通量、照度这些量有点抽象，那么对于我们日常生活最直观的感觉——看到的亮度——其实就是辐亮度在起作用。换句话说，眼睛或者相机看到的亮度，本质上就是场景中表面的辐亮度。

从相机的角度来看，一个像素的亮度取决于它在快门打开期间收到的光能量。简单来说，可以写成：

\[Q = E \cdot S \cdot T\]

$Q$ 是像素积累的光能量
$S$ 是像素的面积
$T$ 是曝光时间
$E$ 是像素表面的照度，也就是单位时间单位面积接受到的光通量

那么，照度 $E$ 又可以用辐亮度表示。直观理解是：像素接收的光是从投射方向来的各种小光束叠加而成的，每束光贡献的能量与它的辐亮度和入射角度有关：

\[E = \int_\boldsymbol{\omega} L(\boldsymbol{p}, \boldsymbol{\omega}) \cos\theta \text{d}\boldsymbol{\omega}\]

$L(\boldsymbol{p},\boldsymbol{\omega})$ 是从方向 $\boldsymbol{\omega}$ 来的辐亮度
$\theta$ 是光线与相机光轴的夹角
对像素格点对应的立体角积分

如果我们把角度积分改成对像素格点面积的积分（这样更直观理解代码中光如何通过像素发射到场景里），可以写成：

\[E = \int_{A_\text{pixel}} L(\boldsymbol{p}, \boldsymbol{\omega}) \cos\theta \frac{\cos\theta \text{d}A}{(f/\cos\theta)^2}\]

于是就自然出现了所谓的 cos⁴规律：

\[E = \int_{A_\text{pixel}} L(\boldsymbol{p}, \boldsymbol{\omega}) \cos^4 \theta \text{d}A\]

这就是为什么广角镜头边缘的亮度常常比中心暗一点，也解释了像素亮度与辐亮度之间的直接联系。

这样，我们就从数学上解释了渲染中的核心计算：像素亮度本质上是相机原点通过像素格点方向上辐亮度的积分。在推导中出现的 $\cos^4\theta$ 项揭示了成像几何带来的能量衰减，而在大多数光线追踪实现中，我们通常忽略这一项，于是计算过程就与经典的光线追踪框架完全一致。

到这里，我们已经完成了从物理量到成像的桥接：渲染要计算的，归根到底就是辐亮度的传输与积分。接下来，自然的问题就是——这些辐亮度从哪里来？它们如何在场景中产生与传播？

19.2 双向散射分布函数（BSDF）

要回答这个问题，我们必须引入一个核心概念：双向散射分布函数（Bidirectional Scattering Distribution Function，BSDF）。它是理解光传输过程的关键枢纽，用来刻画介质表面与光的交互行为。

虽然我们在前两篇文章中已经大量使用了 BSDF 这一概念，但是这里我们借着学习渲染方程，也学习一下其严格的定义。

双向散射分布函数统一描述了材质表面对光的各种散射行为，包括反射（Reflection）和透射（Transmission）。它是一个比率函数，告诉我们某个角度的对应入射光，散射到某个出射方向的比例是多少。

BSDF 可以拆解为两个部分：

双向反射分布函数（BRDF）：描述材质对入射光的反射行为。

双向透射分布函数（BTDF）：描述材质对入射光的透射行为。

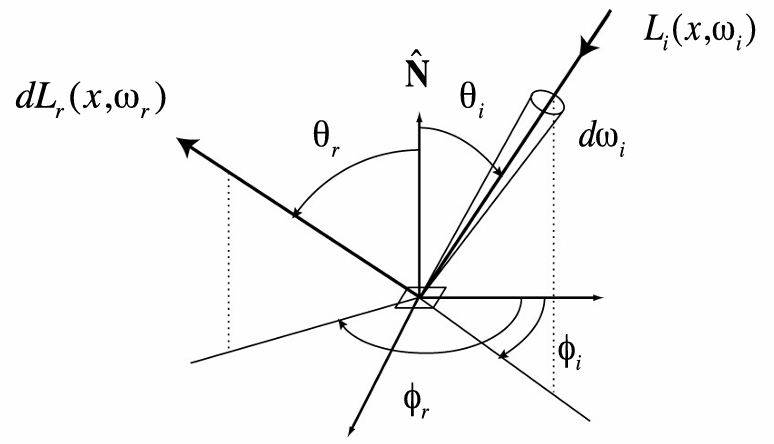
直观理解是：来自方向 $\boldsymbol{\omega}_i$ 的辐亮度，首先转化为表面微元 $\text{d}A$ 接收到的功率 $E$，然后这部分功率再通过 BSDF 分配，成为任意出射方向 $\boldsymbol{\omega}_o$ 上的辐亮度。

其严格定义如下：

对于入射方向 $\boldsymbol{\omega}_i$，表面接收到的微分辐照度为

\[\text{d}E_i(\boldsymbol{p}, \boldsymbol{\omega}_i) = L_i(\boldsymbol{p}, \boldsymbol{\omega}_i) \cos\theta_i \text{d}\boldsymbol{\omega}_i\]

接着，BSDF 决定这部分能量中有多少分配到出射方向 $\boldsymbol{\omega}_o$ 上：

\[f_s(\boldsymbol{p}, \boldsymbol{\omega}_i, \boldsymbol{\omega}_o) = \frac{\text{d}L_o(\boldsymbol{p}, \boldsymbol{\omega}_o)}{\text{d}E_i(\boldsymbol{p}, \boldsymbol{\omega}_i)} = \frac{\text{d}L_o(\boldsymbol{p}, \boldsymbol{\omega}_o)}{L_i(\boldsymbol{p}, \boldsymbol{\omega}_i) \cos\theta_i \text{d}\boldsymbol{\omega}_i}\ \left[\frac{1}{\text{sr}}\right]\]

BSDF 的几个重要性质：

能量守恒：不能凭空产生能量，即所有散射出去的光不超过入射光。
互易性（Reciprocity）：$f_s(\boldsymbol{\omega}_i, \boldsymbol{\omega}_o) = f_s(\boldsymbol{\omega}_o, \boldsymbol{\omega}_i)$，物理上光的传播路径是可逆的。
方向依赖：不同材质在不同角度可能表现完全不同，比如镜面反射、漫反射、半透明等。

在实际渲染中，我们常见的材质模型（Lambertian 漫反射、Phong 高光、GGX 微平面模型等），本质上都是对 BSDF 的具体近似。

BSDF 给出了入射光如何转化为出射光的局部规律：来自某一方向 $\boldsymbol{\omega}_i$ 的辐亮度 $L_i$，经过介质表面的作用，会贡献一部分出射到方向 $\boldsymbol{\omega}_o$ 的辐亮度。把这种关系写下来，再对所有可能的入射方向 $\boldsymbol{\omega}_i$ 进行积分，我们就得到了描述全局能量传输的核心公式——渲染方程。

19.3 渲染方程

渲染方程（Rendering Equation）由 James Kajiya 在 1986 年提出，它是描述光能传输的统一数学形式。它刻画了某点在某个方向上的出射辐亮度 $L_o$ 与该点的自发光和所有入射方向上的辐亮度之间的关系：

\[L_o(\boldsymbol{p}, \boldsymbol{\omega}_o) = L_e(\boldsymbol{p}, \boldsymbol{\omega}_o) + \int_{\mathbb{S}^2} f_s(\boldsymbol{p}, \boldsymbol{\omega}_i, \boldsymbol{\omega}_o)\, L_i(\boldsymbol{p}, \boldsymbol{\omega}_i)\, |\boldsymbol{n}\cdot \boldsymbol{\omega}_i|\, d\boldsymbol{\omega}_i\]

其中：

$\boldsymbol{p}$：空间中的表面点；
$\boldsymbol{\omega}_o$：出射方向；
$\boldsymbol{\omega}_i$：入射方向；
$L_o$：出射辐亮度（最终进入相机、决定像素亮度的量）；
$L_e$：自发光项（如灯泡或发光材质的直接贡献）；
$L_i$：入射辐亮度（来自场景中其他位置的光）；
$f_s$：BSDF（双向散射分布函数），描述从 $\boldsymbol{\omega}_i$ 入射的光中，有多少能量被散射到 $\boldsymbol{\omega}_o$ 出射方向；
$|\boldsymbol{n}\cdot \boldsymbol{\omega}_i|$：余弦项，体现入射角度对受光面积的影响；
$\mathbb{S}^2$：单位球面，即所有可能的入射方向。

这条方程的含义是：一个点向外发出的光亮度，等于它本身的自发光，加上来自所有方向的入射光经由材质散射之后的贡献。

换句话说，渲染方程就是图形学中光传输的“第一性原理”。我们接下来会看到的各种光线追踪算法、蒙特卡罗积分方法，以及后续的加速与近似技巧，都是在尝试以更高效或更可控的方式去近似求解这条积分方程。

19.4 蒙特卡罗方法

渲染方程的形式虽然简洁，但它本质上是一个积分方程。对于任意复杂场景和材质，想要解析求解几乎不可能，原因很直观：

入射辐亮度 $L_i$ 本身依赖于场景中其他点的出射辐亮度 $L_o$，需要递归计算；
场景几何和材质可能复杂到无法写成显式表达式；
积分范围是整个半球，涉及到高维积分（递归传输会进一步导致维度上升）。

这意味着我们必须使用数值方法来近似计算，而图形学中最自然的数值方法，就是蒙特卡罗积分（Monte Carlo Integration）。

蒙特卡罗积分的基本思想

设有一个积分：

\[I = \int_\boldsymbol{\omega} f(x) dx\]

如果从积分区域 $\boldsymbol{\omega}$ 中根据概率密度函数 $p(x)$ 采样 $N$ 个样本 $x_i$，则可以得到无偏估计：

\[I \approx \frac{1}{N} \sum_{i=1}^N \frac{f(x_i)}{p(x_i)}\]

这就是蒙特卡罗方法的核心思想：把积分转化为随机采样的平均值。它的方差会随样本数 $N$ 的增加而下降，最终收敛到真实结果。

换句话说，蒙特卡罗方法用随机性换来了普适性：不管积分有多复杂、多高维，只要能随机采样，就能近似它。

应用到渲染方程

把渲染方程写出来：

这正是一个典型的积分形式：积分域是半球，积分函数包含入射辐亮度、BSDF 和几何因子。我们无法解析解，但可以通过随机采样入射方向 $\boldsymbol{\omega}_i$ 来近似：

\[L_o(\boldsymbol{p}, \boldsymbol{\omega}_o) \approx L_e(\boldsymbol{p}, \boldsymbol{\omega}_o) + \frac{1}{N}\sum_{i=1}^N \frac{ f_s(\boldsymbol{p}, \boldsymbol{\omega}_i, \boldsymbol{\omega}_o)\, L_i(\boldsymbol{p}, \boldsymbol{\omega}_i)\, |\boldsymbol{n}\cdot \boldsymbol{\omega}_i| }{p(\boldsymbol{\omega}_i)}\]

其中 $p(\boldsymbol{\omega}_i)$ 就是采样入射方向的概率密度函数。

这意味着，只要我们能不断采样入射方向并估计贡献，最终就能逼近真实的出射辐亮度。

路径跟踪算法

将蒙特卡罗积分的思想应用到渲染方程，就得到了 路径跟踪（Path Tracing）。虽然在前面的实现中我们已经以较为经验性的方式使用过路径跟踪，但那时并没有严格地建立在数学公式的基础之上。这里，我们是第一次从渲染方程的数学形式出发，对路径跟踪算法进行严谨的推导和表述。其基本流程可以总结为：

从相机像素发射一条光线。
找到与场景的交点，累加该点的自发光。
随机采样一个新的入射方向（可以从任何分布，由 BSDF 决定的是重要性采样，下一节介绍）。
更新路径的权重，即乘上
\[\frac{f(\boldsymbol{p}, \boldsymbol{\omega}_o, \boldsymbol{\omega}_i)\,|\boldsymbol{n}\cdot \boldsymbol{\omega}_i|}{p(\boldsymbol{\omega}_i)},\]
其中 $f$ 为 BSDF，$p$ 为采样该方向的概率密度。
重复以上步骤，直到光线逃逸场景或达到弹射上限。

最终，一个像素的亮度就是许多条这样的随机路径的平均结果。

在代码层面，我们可以这样实现一个随机游走路径跟踪器：

@ti.data_oriented
class RandomWalkPathIntegrator(PathIntegrator):
    def __init__(self, propagate_limit, BSDF_importance_sampling=True):
        self.propagate_limit = propagate_limit
        self.BSDF_importance_sampling = BSDF_importance_sampling
                
    @ti.func
    def run(self, ray: ti.template(), world: ti.template()):
        bounce = 0
        L = Vec3f(0.0)     # 累积辐亮度
        beta = Vec3f(1.0)  # 路径权重
        
        while True:
            # 1. 相交
            record = world.hit(ray)
            if record.prim_type == PrimitiveType.UNHIT:
                # 环境光
                L += beta * world.env.sample(ray.rd)
                break
                
            # 2. 加上自发光
            L += beta * record.si.emission
            
            # 3. 终止条件
            bounce += 1
            if bounce >= self.propagate_limit:
                break
                
            # 4. BSDF 采样一个方向
            bm, wi, pdf = DiffuseBSDF.sample(
                -ray.rd, record.si,
                use_importance_sampling=self.BSDF_importance_sampling
            )
            ray.ro = record.si.point
            ray.rd = wi
            beta *= bm
            
            # 5. 权重衰减到零则终止
            if beta.norm() < 1e-8:
                break
                
        return L

与前一章“经验性弹射”的差别在于：这里每一次弹射，路径权重 beta 的更新严格遵循渲染方程，保证了算法的物理一致性。

这样，一个完整的随机游走路径跟踪器就建立起来了。

19.5 重要性采样

在路径追踪中，每次弹射时都需要随机选择一个新的入射方向 $\boldsymbol{\omega}_i$。最直接的办法是 均匀采样 半球，即每个方向出现的概率相同。这样做虽然实现简单，但问题在于：渲染方程的被积函数往往并不是均匀的，而是由 $f(\boldsymbol{p}, \boldsymbol{\omega}_o, \boldsymbol{\omega}_i)\ |\boldsymbol{n}\cdot \boldsymbol{\omega}_i|$ 决定的。在一些方向上贡献很大，而在另一些方向上几乎为零。如果仍然均匀采样，就会把大量计算浪费在贡献很小的方向上，从而导致估计方差很高、收敛很慢。

重要性采样（Importance Sampling） 的思想就是：尽量让采样分布 $p(\boldsymbol{\omega}_i)$ 与被积函数的形状接近，这样高贡献的方向会被更频繁地采到，从而降低方差。

在蒙特卡罗估计中，每次弹射时路径的权重因子为：

\[\frac{f(\boldsymbol{p}, \boldsymbol{\omega}_o, \boldsymbol{\omega}_i)\,|\boldsymbol{n}\cdot \boldsymbol{\omega}_i|}{p(\boldsymbol{\omega}_i)}.\]

因此，只要让这个因子尽可能和 $\boldsymbol{\omega}_i$ 无关，所有样本的贡献相等，积分的结果就会更加稳定，噪声显著减少。

这里我们以漫反射表面为例。之前我们提到，对于漫反射表面，BSDF 为

\[f(\boldsymbol{\omega}_o, \boldsymbol{\omega}_i) = \frac{\text{albedo}}{\pi}\quad\text{for}\ \boldsymbol{n} \cdot \boldsymbol{\omega}_i > 0，\]

为常数，对应路径积分中的权重因子为：

\[\frac{f(\boldsymbol{p}, \boldsymbol{\omega}_o, \boldsymbol{\omega}_i)\,|\boldsymbol{n}\cdot \boldsymbol{\omega}_i|}{p(\boldsymbol{\omega}_i)} = \frac{\text{albedo}\,\cos\theta_i}{\pi\ p(\boldsymbol{\omega}_i)}\]

于是理想的采样分布就是余弦加权分布 $p(\boldsymbol{\omega}_i) = \cos\theta / \pi$。

class DiffuseBSDF:
    @staticmethod
    @ti.func
    def f(wo, wi, si: ti.template()):
        # 漫反射的 BRDF：f(wo, wi) = albedo / π
        return si.albedo / ti.pi

    @staticmethod
    @ti.func
    def sample(wo, si: ti.template(), use_importance_sampling):
        bm = Vec3f(0.0)  # 当前弹射方向的路径权重贡献 (f * cosθ / p)
        wi = Vec3f(0.0)  # 采样得到的入射方向
        pdf = 0.0        # 该方向的采样概率密度
        n = si.normal
        # 建立切线空间坐标系 (t, b, n)，用于采样半球方向
        t, b = _get_tangent_space(n)

        if use_importance_sampling:
            # -----------------------------
            # 余弦加权采样（重要性采样）
            # -----------------------------
            # 采样分布：p(wi) = cosθ / π
            wi = _sample_hemisphere_cosine_weighted(t, b, n)
            pdf = max(0.0, si.normal.dot(wi)) / ti.math.pi

            # 权重因子： (f * cosθ) / p(wi)
            # = (albedo / π * cosθ) / (cosθ / π) = albedo
            bm = si.albedo

        else:
            # -----------------------------
            # 半球均匀采样
            # -----------------------------
            # 采样分布：p(wi) = 1 / (2π)
            wi = _sample_hemisphere_uniform(t, b, n)
            pdf = 1.0 / (2.0 * ti.math.pi)

            # 权重因子： (f * cosθ) / p(wi)
            # = (albedo / π * cosθ) / (1 / 2π)
            # = albedo * 2cosθ
            bm = si.albedo * (2 * max(0.0, si.normal.dot(wi)))

        # 如果采样方向落到几何法线的背面，则反射回去，避免漏光
        if wi.dot(si.geo_normal) < 0:
            wi = _reflect(wi, si.geo_normal)

        return bm, wi, pdf

19.6 效果对比

为了验证重要性采样的效果，我们在 Cornell Box 场景中分别使用 均匀采样 与 重要性采样 进行渲染。Cornell Box 是计算机图形学中最常用的测试场景之一，场景介绍与模型数据可参考 Cornell Box Data。

实验设置：

场景：Cornell Box

材质：漫反射

每像素采样数：8192 spp

路径跟踪算法：随机游走

采样策略：均匀采样 vs. 重要性采样

下图展示了在相同采样数下两种方法的效果对比。左图为 均匀采样，由于大量样本落在几乎无贡献的方向上，导致图像噪声明显；右图为 余弦加权的重要性采样，采样分布与被积函数形状相匹配，更频繁采到高贡献方向，因此噪声显著减少，收敛速度更快。

20. 微平面材质模型

在第一篇文章里，我们已经用直观的方式介绍过 微平面模型（Microfacet Model） 的主要思想：粗糙表面可以看作是由大量微小的镜面片段组成，每个微平面按照镜面反射定律反射光线。表面的整体反射效果，就来自于这些微平面的 朝向分布、几何遮挡 以及 菲涅尔效应（Fresnel Effect） 的综合作用。只是当时我们未能从 BRDF 的角度给出其严格的数学定义。这也导致了我们当时的渲染结果与 Blender 的 Cycles 有明显的不一致。

这一节中，我们将沿着这一条从物理出发的路径，去建立一个更真实的材质反射模型。

20.1 法线分布函数

在微平面模型中，我们把宏观表面想象成由无数微小的“镜面碎片”组成。每一片微平面都有自己的法线方向，而这些方向 并不完全相同——表面越粗糙，法线分布越分散；表面越光滑，法线越集中。

这种统计特性由 法线分布函数（Normal Distribution Function，NDF） $D(\boldsymbol{h})$ 来描述。它定义为单位面积表面上法线朝向 $\boldsymbol{h}$ 的微平面比例：

\[D(\boldsymbol{h}) = \lim_{\text{d}\boldsymbol{\omega}_h \to 0} \frac{\text{P}(\boldsymbol{\omega} \in \boldsymbol{h} + \text{d}\boldsymbol{\omega}_h)}{\text{d}\boldsymbol{\omega}_h}.\]

法线分布函数满足归一化条件：

\[\int_{\Omega^+} D(\boldsymbol{h})\ (\boldsymbol{n} \cdot \boldsymbol{h})\ \text{d}\boldsymbol{\omega}_h = 1,\]

其中：

$\boldsymbol{n}$：宏观表面法线
$\boldsymbol{h}$：微平面法线
$\Omega^+$：与宏观法线形成锐角的半球区域

直观地说，这意味着所有微平面在宏观表面上的投影面积总和占满了整个表面。

常见法线分布函数

1. Beckmann 分布

Beckmann 分布常用于光滑或抛光表面。它的高光尖锐集中，能够很好地模拟镜面反射：

\[D_{\text{Beckmann}}(\boldsymbol{h}) = \frac{1}{\pi \alpha^2 \cos^4\theta_h} \exp\Big(-\frac{\tan^2\theta_h}{\alpha^2}\Big),\]

其中 $\theta_h$ 为微平面法线与宏观法线的夹角，$\alpha$ 为粗糙度参数，值越小表示表面越光滑。

2. GGX / Trowbridge-Reitz 分布

GGX 分布在现代 PBR 渲染中应用广泛。相比 Beckmann，它的高光更柔和，具有长尾效果，更适合表现粗糙表面：

\[D_{\text{GGX}}(\boldsymbol{h}) = \frac{\alpha^2}{\pi \big[(\cos^2\theta_h)(\alpha^2 - 1) + 1\big]^2}.\]

GGX 的特点是高光柔和、尾部长，计算效率高，非常适合实时渲染和游戏引擎使用。

20.2 几何遮挡函数

在微平面模型中，并非每一个微平面都能完全反射光线到观察方向。微平面之间可能会 互相遮挡或自遮挡：当一个微平面被邻近微平面挡住时，它对宏观表面的反射贡献就会减小。为了描述这种现象，我们引入 几何遮挡函数（Geometric Attenuation Function） $G(\boldsymbol{\omega}_i, \boldsymbol{\omega}_o)$。

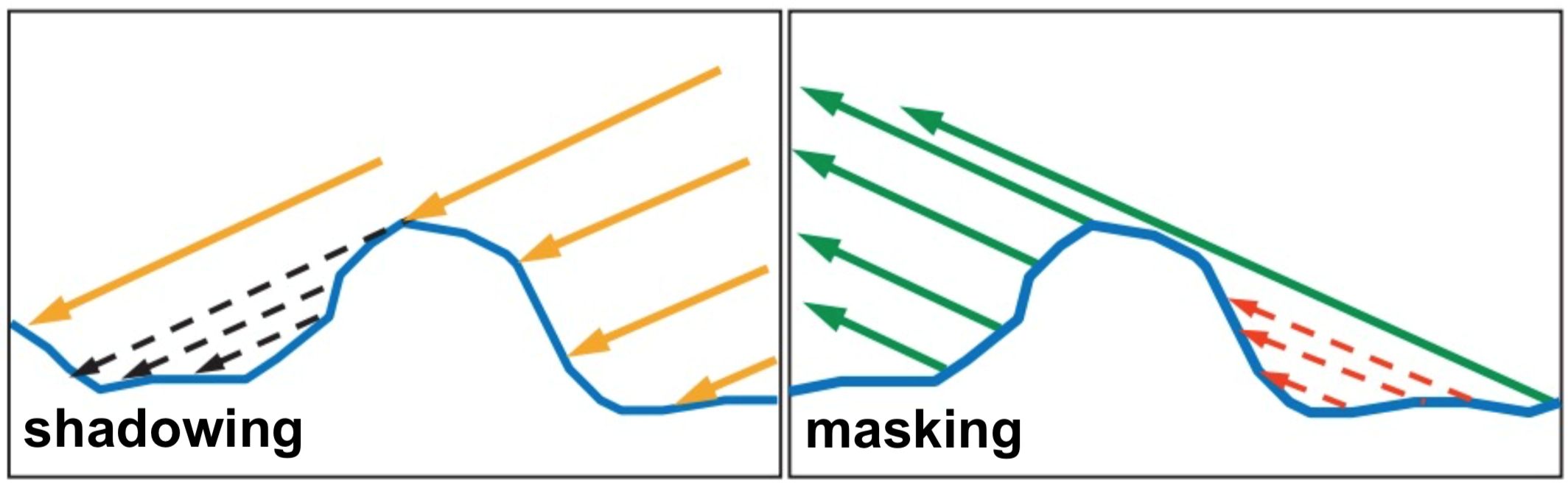
几何遮挡函数的值通常介于 0 到 1 之间，表示微平面能有效反射光的概率：

$G = 1$ 表示无遮挡，微平面完全可见
$G = 0$ 表示完全遮挡，无光线反射

物理直观地理解：$G$ 反映了宏观表面上，朝向入射方向 $\boldsymbol{\omega}_i$ 和出射方向 $\boldsymbol{\omega}_o$ 的微平面中，能够同时看到光源和观察方向的那一部分微平面比例。

常见几何遮挡模型

1. V-Cavity 遮蔽模型

在早期的微平面理论研究中，人们提出过一种理想化的遮挡模型：假设表面由无数 V 型槽 组成（就像规则排列的小山谷），光线只能在这些槽的开口中反射出来。这就是 V-Cavity 模型。

在这种假设下，几何遮挡函数可以简化为：

\[G_{\text{V-Cavity}}(\boldsymbol{\omega}_i, \boldsymbol{\omega}_o) = \min \Big(1,\ \frac{2 (\boldsymbol{n}\cdot \boldsymbol{h}) (\boldsymbol{n}\cdot \boldsymbol{\omega}_o)}{(\boldsymbol{\omega}_o \cdot \boldsymbol{h})},\ \frac{2 (\boldsymbol{n}\cdot \boldsymbol{h}) (\boldsymbol{n}\cdot \boldsymbol{\omega}_i)}{(\boldsymbol{\omega}_i \cdot \boldsymbol{h})} \Big).\]

直观上，V-Cavity 模型认为：当入射或出射方向过于倾斜时，微平面就会被 “槽壁” 遮住，因此贡献被削弱。

2. Smith 遮挡函数

相比理想化的 V-Cavity 模型，Smith 遮挡函数是一种更为通用且高效的近似方法。它将入射方向和出射方向的遮挡效应分别建模，再将二者相乘得到整体几何项：

\[G(\boldsymbol{\omega}_i, \boldsymbol{\omega}_o) = G_1(\boldsymbol{\omega}_i) \cdot G_1(\boldsymbol{\omega}_o),\]

其中 $G_1$ 表示单方向的可见性函数。例如对于 GGX 分布，$G_1$ 可以写成：

\[G_1(\boldsymbol{\omega}) = \frac{2 (\boldsymbol{n} \cdot \boldsymbol{\omega})}{(\boldsymbol{n} \cdot \boldsymbol{\omega}) + \sqrt{\alpha^2 + (1 - \alpha^2)(\boldsymbol{n} \cdot \boldsymbol{\omega})^2}}.\]

这里 $\alpha$ 是表面粗糙度参数。

通过几何遮挡函数，我们就能在微平面 BRDF 中引入微观自遮挡的影响，使高光更加真实：光滑表面几乎无遮挡，高光尖锐；粗糙表面遮挡明显，高光分布变宽且衰减。

20.3 菲涅尔效应

菲涅尔效应我们在第一章已经提到过：当光线以较小的角度 掠过表面 时，反射率会显著增强。这种现象由 菲涅尔方程（Fresnel Equations） 精确描述，它决定了光在两种介质界面上如何分配为反射和折射。

物理上，菲涅尔效应解释了为什么水面、玻璃或金属在较大入射角时看起来更加镜面、更加“亮”。

菲涅尔方程

严格的菲涅尔方程需要用入射角 $\theta_i$ 和相对折射率 $\eta = \eta_\text{ext}/\eta_\text{int}$ 来计算平行（$\parallel$）和垂直（$\perp$）两种偏振状态下的反射率：

\[F_\perp(\theta_i) = \left(\frac{\eta \cos \theta_i - \cos \theta_t}{\eta \cos \theta_i + \cos \theta_t}\right)^2, \quad F_\parallel(\theta_i) = \left(\frac{\cos \theta_i - \eta \cos \theta_t}{\cos \theta_i + \eta \cos \theta_t}\right)^2,\]

总体反射率为：

\[F(\theta_i) = \frac{F_\perp(\theta_i) + F_\parallel(\theta_i)}{2}.\]

这里 $\theta_t$ 是折射角，由 斯涅尔定律 $\eta \sin \theta_i = \sin \theta_t$ 得到。

虽然这是最精确的公式，但在实时渲染中代价较高。

Schlick 近似

为了兼顾效率和视觉效果，我们通常采用 Schlick 近似 来简化计算：

\[F(\boldsymbol{\omega}_i, \boldsymbol{h}) \approx F_0 + (1 - F_0)(1 - \boldsymbol{\omega}_i \cdot \boldsymbol{h})^5,\]

其中：

$F_0$ 表示正入射（$\theta_i = 0$）时的反射率，通常由材质的折射率决定。
$\boldsymbol{\omega}_i \cdot \boldsymbol{h}$ 表示入射方向与半程向量的夹角余弦。

这个近似公式虽然简单，却能很好地拟合真实的菲涅尔曲线，因此被广泛应用于游戏引擎和实时 PBR 渲染中。

20.4 微平面 BRDF

利用前面介绍的三个组成部分（$D$、$G$、$F$），我们可以把微平面理论写成完整的 BRDF 形式。

首先回顾 BRDF 的定义：它描述了入射辐照度对出射辐亮度的贡献关系。对于某个表面点 $\boldsymbol{p}$，考虑入射方向 $\boldsymbol{\omega}_i$ 的微分辐照度

\[\text{d}E_i(\boldsymbol{p}, \boldsymbol{\omega}_i) = L_i(\boldsymbol{p}, \boldsymbol{\omega}_i)\ (\boldsymbol{n}\cdot\boldsymbol{\omega}_i)\ \text{d}\boldsymbol{\omega}_i,\]

以及对应的出射微分辐亮度

\[\text{d}L_o(\boldsymbol{p}, \boldsymbol{\omega}_o).\]

根据定义，BRDF 写为：

\[f_r(\boldsymbol{p}, \boldsymbol{\omega}_i, \boldsymbol{\boldsymbol{\omega}}_o) = \frac{\text{d}L_o(\boldsymbol{p}, \boldsymbol{\omega}_o)}{L_i(\boldsymbol{p}, \boldsymbol{\omega}_i)\ (\boldsymbol{n}\cdot\boldsymbol{\omega}_i)\ \text{d}\boldsymbol{\omega}_i}\]

在微平面模型中，所有宏观反射均被视为是由微观的微平面的镜面反射统计形成。对于入射方向 $\boldsymbol{\omega}_i$，出射方向 $\boldsymbol{\omega}_o$，其宏观反射由法线为 $\boldsymbol{h}$ 的微平面形成，如图所示:

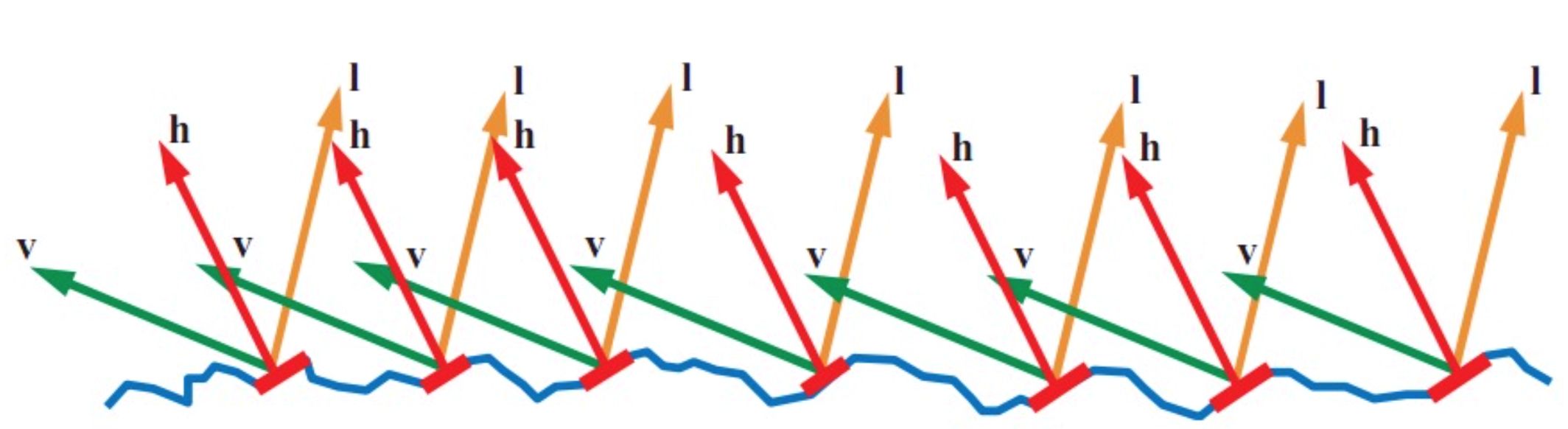
其中微平面法线为半程向量

\[\boldsymbol{h} = \frac{\boldsymbol{\omega}_i + \boldsymbol{\omega}_o}{\|\boldsymbol{\omega}_i + \boldsymbol{\omega}_o\|}.\]

这部分微平面接收到的微分辐射通量为：

\[\text{d}^3\Phi = \underbrace{D(\boldsymbol{h})\ \text{d}\boldsymbol{h}\ \text{d}A}_{\text{微平面的微分面积}} \cdot \underbrace{(\boldsymbol{h}\cdot\boldsymbol{\omega}_i)}_{\text{投影到入射方向}} \cdot \underbrace{L_i(\boldsymbol{p}, \boldsymbol{\omega}_i)\ \text{d}\boldsymbol{\omega}_i}_{\text{入射微分垂直辐射照度}}\]

因为镜面反射，所以出射方向上的通量与入射一致，且对应球面角微元相等，对应微分辐亮度可以写成

\[\text{d} L_o(\boldsymbol{p}, \boldsymbol{\omega}_o) = \frac{D(\boldsymbol{h})\ L_i(\boldsymbol{p}, \boldsymbol{\omega}_i)\ (\boldsymbol{h}\cdot\boldsymbol{\omega}_i)\ \text{d}\boldsymbol{\omega}_i\ \text{d}\boldsymbol{h}\ \text{d}A}{(\boldsymbol{n}\cdot\boldsymbol{\omega}_o)\ \text{d}\boldsymbol{\omega}_o\ \text{d}A}\]

约分整理得到

代入 BRDF 的定义式，得到

\[f_r(\boldsymbol{p}, \boldsymbol{\omega}_i, \boldsymbol{\boldsymbol{\omega}}_o) = \frac{D(\boldsymbol{h})\ (\boldsymbol{h}\cdot\boldsymbol{\omega}_i)\ \text{d}\boldsymbol{h}}{(\boldsymbol{n}\cdot\boldsymbol{\omega}_i)\ (\boldsymbol{n}\cdot\boldsymbol{\omega}_o)\ \text{d}\boldsymbol{\omega}_i}\]

考察半程向量球面微元和入射方向球面微元的关系：

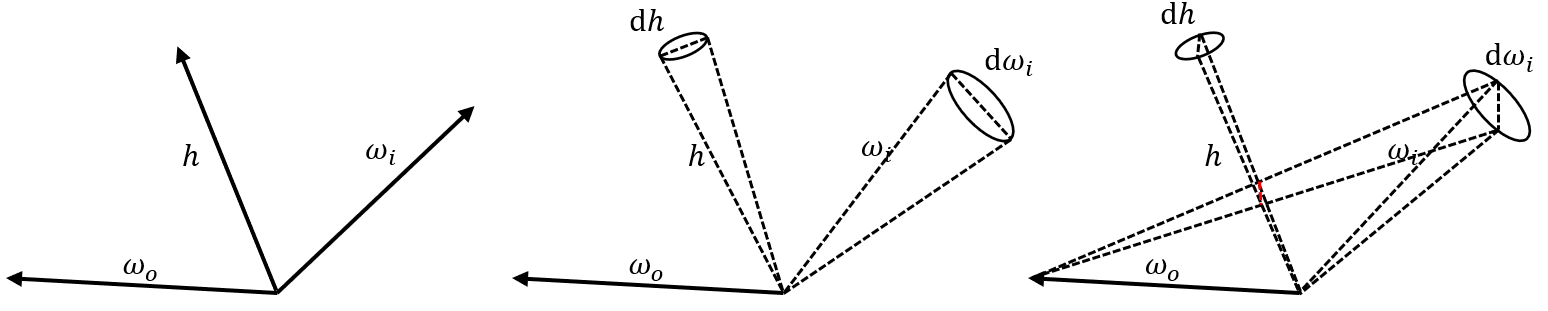
如图所示，对于平行于反射平面上的长度 $x$（中图），

\[\text{d}x_h = \frac{1}{2} \text{d}x_i\]

对于垂直于反射平面上的长度 $y$（右图），

\[\text{d}y_h = \frac{1}{2(\boldsymbol{h}\cdot\boldsymbol{\omega}_i)} \text{d}y_i\]

最终有

\[\text{d}\boldsymbol{h} = \frac{1}{4 (\boldsymbol{h}\cdot\boldsymbol{\omega}_i)} \text{d}\boldsymbol{\omega}_i\]

代入 BRDF 的定义式，得到

\[f_r(\boldsymbol{p}, \boldsymbol{\omega}_i, \boldsymbol{\boldsymbol{\omega}}_o) = \frac{D(\boldsymbol{h})}{4\ (\boldsymbol{n}\cdot\boldsymbol{\omega}_i)\ (\boldsymbol{n}\cdot\boldsymbol{\omega}_o)}\]

最后，我们再将几何遮挡与菲涅尔效应考虑进来，得到完整的微平面 BRDF：

\[f_r(\boldsymbol{p}, \boldsymbol{\omega}_i, \boldsymbol{\boldsymbol{\omega}}_o) = \frac{F(\boldsymbol{\omega}_i, \boldsymbol{h})\ D(\boldsymbol{h})\ G(\boldsymbol{\omega}_i, \boldsymbol{\omega}_o)}{4\ (\boldsymbol{n}\cdot\boldsymbol{\omega}_i)\ (\boldsymbol{n}\cdot\boldsymbol{\omega}_o)}\]

20.5 Principled BRDF 实现

在前面，我们已经分别介绍了微平面模型的三个核心部分：法线分布函数 $D$、几何遮挡函数 $G$ 和菲涅尔效应 $F$。在具体实现时，需要为这些函数选择合适的形式。

目前在实时渲染和离线渲染中最常用的组合是：

法线分布函数 $D$：采用 GGX 分布，它在大角度处衰减较慢，能更好地表现粗糙材质的长尾高光。
几何遮挡函数 $G$：采用 Smith-GGX 形式，兼顾了精度和计算效率。
菲涅尔项 $F$：使用 Schlick 近似，高效且足够精确。

粗糙度系数 $\alpha$ 定义为供艺术家调节的粗糙度 $\text{roughness}$ 的平方。

这样的选择在物理一致性和实际可用性之间取得了良好的平衡，因此被广泛作为 “principled” 的基础实现。

接下来我们就将这些要素组合起来，写出最终的 BRDF 形式，并讨论在代码中的实现细节。

@ti.func
def _schlick_fresnel(cos_theta):
    # Schlick 近似：F(θ) ≈ F0 + (1-F0)(1-cosθ)^5
    # 这里只返回 (1-cosθ)^5 部分，F0 在外部结合
    one_minus = 1.0 - cos_theta
    factor = one_minus * one_minus
    factor = factor * factor * one_minus
    return factor


@ti.func
def _reflect(dir, normal):
    # 向量反射公式：r = d - 2(d·n)n
    k = -dir.dot(normal)
    r = dir + 2 * k * normal
    return r


@ti.func
def _D_GGX(ndoth, alpha):
    # GGX 法线分布函数 D(h)
    out = 0.0
    if ndoth > 0.0:
        a2 = alpha * alpha
        ndoth2 = ndoth * ndoth
        denom = ndoth2 * (a2 - 1.0) + 1.0
        denom = ti.math.pi * denom * denom
        out = a2 / max(denom, 1e-16)
    return out
    

@ti.func
def _G1_GGX(ndotv, alpha):
    # GGX 的单向遮蔽项 G1(v)
    # Smith 公式：2 / (1 + sqrt(1 + a^2 * tan^2θ))
    out = 0.0
    if ndotv > 0.0:
        cos2 = ndotv * ndotv
        sin2 = ti.max(0.0, 1.0 - cos2)
        tan2 = sin2 / cos2
        a2 = alpha * alpha
        out = 2.0 / (1.0 + ti.sqrt(1.0 + a2 * tan2))
    return out


@ti.func
def _G_smith(cos_i, cos_o, alpha):
    # Smith 遮挡函数：G = G1(ωi) * G1(ωo)
    return _G1_GGX(cos_i, alpha) * _G1_GGX(cos_o, alpha)


@ti.func
def _sample_hemisphere_ggx_h(t, b, n, alpha):
    # GGX 半程向量采样
    u1 = ti.random(ti.f32)
    u2 = ti.random(ti.f32)
    cos2_theta = (1.0 - u1) / (1.0 + (alpha*alpha - 1.0) * u1)
    cos_theta = ti.sqrt(cos2_theta)
    sin_theta = ti.sqrt(1.0 - cos2_theta)
    phi = 2.0 * ti.math.pi * u2
    local_dir = Vec3f([sin_theta * ti.cos(phi), sin_theta * ti.sin(phi), cos_theta])
    return t * local_dir.x + b * local_dir.y + n * local_dir.z


@ti.func
def _lum(c):
    # 计算颜色亮度，用于重要性采样的加权
    return 0.2126 * c.x + 0.7152 * c.y + 0.0722 * c.z


class PrincipledBSDF:
    @staticmethod
    @ti.func
    def f(wo, wi, si: ti.template()):
        # BSDF 评估函数：返回给定入射 wi 和出射 wo 的反射率
        f = Vec3f(0.0)
        n = si.normal
        h = (wi + wo).normalized()
        cos_o = n.dot(wo)
        cos_i = n.dot(wi)
        cos_half = h.dot(wi)
        ndoth = n.dot(h)
        f_factor = _schlick_fresnel(cos_half)
        Fd0 = ((si.ior - 1) / (si.ior + 1))**2  # 基础菲涅尔反射率 (非金属)

        # ---------- 镜面项 ----------
        denom = 4.0 * cos_i * cos_o
        if denom > 1e-8:
            alpha = si.roughness * si.roughness
            F0 = si.metallic * si.albedo + (1.0 - si.metallic) * Fd0
            ## 法线分布项
            D = _D_GGX(ndoth, alpha)
            ## 菲涅尔项
            F = F0 + (1.0 - F0) * f_factor
            ## 几何遮挡项
            G = _G_smith(cos_i, cos_o, alpha)
            f += (D * F * G) / denom
            
        # ---------- 漫反射项 ----------
        Fd = Fd0 + (1.0 - Fd0) * f_factor
        f += (1.0 - si.metallic) * (1 - Fd) * si.albedo / ti.math.pi
        
        return f
    
    @staticmethod
    @ti.func
    def pdf(wo, wi, si: ti.template(), use_importance_sampling):
        # 返回给定方向对的采样概率密度函数
        pdf = 0.0
        n = si.normal
        if use_importance_sampling:
            cos_o = n.dot(wo)
            Fd0 = ((si.ior - 1) / (si.ior + 1))**2
            F0 = si.metallic * si.albedo + (1.0 - si.metallic) * Fd0
            
            # ---------- 特殊情况：完美镜面 ----------
            if si.roughness == 0.0:
                f_factor = _schlick_fresnel(cos_o)
                F = F0 + (1.0 - F0) * f_factor
                Fd = Fd0 + (1.0 - Fd0) * f_factor
                T = (1 - si.metallic) * (1 - Fd) * si.albedo
                F_lum = _lum(F)
                T_lum = _lum(T)
                p_F = F_lum / (F_lum + T_lum)
                p_T = 1.0 - p_F
                pdf = p_T * wi.dot(n) / ti.math.pi
                
            # ---------- 一般情况：GGX + Lambert ----------
            else:
                T0 = (1.0 - si.metallic) * (1.0 - Fd0) * si.albedo
                F_lum = _lum(F0)
                T_lum = _lum(T0)
                p_F = F_lum / (F_lum + T_lum)
                p_T = 1.0 - p_F
                alpha = si.roughness * si.roughness
                h = (wi + wo).normalized()
                cos_i = n.dot(wi)
                cos_half = h.dot(wi)
                ndoth = n.dot(h)                    
                D = _D_GGX(ndoth, alpha)
                pdf_ggx = D * ndoth / (4.0 * cos_half)
                pdf_lambert = cos_i / ti.math.pi
                pdf = p_F * pdf_ggx + p_T * pdf_lambert               
        else:
            # 均匀采样半球
            pdf = 1.0 / (2.0 * ti.math.pi)
        
        return pdf
    
    @staticmethod
    @ti.func
    def sample(wo, si: ti.template(), use_importance_sampling):
        # 给定出射方向 wo，采样一个入射方向 wi，并返回贡献 bm 和 pdf
        bm = Vec3f(0.0)
        wi = Vec3f(0.0)
        pdf = 1.0
        n = si.normal
        t, b = _get_tangent_space(n)
        if use_importance_sampling:
            cos_o = n.dot(wo)
            Fd0 = ((si.ior - 1) / (si.ior + 1))**2
            F0 = si.metallic * si.albedo + (1.0 - si.metallic) * Fd0
            
            # ---------- 完美镜面 ----------
            if si.roughness == 0.0:
                f_factor = _schlick_fresnel(cos_o)
                F = F0 + (1.0 - F0) * f_factor
                Fd = Fd0 + (1.0 - Fd0) * f_factor
                T = (1 - si.metallic) * (1 - Fd) * si.albedo
                F_lum = _lum(F)
                T_lum = _lum(T)
                p_F = F_lum / (F_lum + T_lum)
                p_T = 1.0 - p_F
                if ti.random(ti.f32) < p_F:
                    wi = _reflect(-wo, n)
                    pdf = ti.math.inf   # delta 分布
                    bm = F / p_F
                else:
                    wi = _sample_hemisphere_cosine_weighted(t, b, n)
                    pdf = p_T * wi.dot(n) / ti.math.pi
                    bm = T / p_T
            
            # ---------- GGX + 漫反射 ----------
            else:
                T0 = (1.0 - si.metallic) * (1.0 - Fd0) * si.albedo
                F_lum = _lum(F0)
                T_lum = _lum(T0)
                p_F = F_lum / (F_lum + T_lum)
                p_T = 1.0 - p_F
                alpha = si.roughness * si.roughness
            
                # 混合采样：GGX 半程向量 or Cosine-weighted
                h = Vec3f(0.0)
                if ti.random(ti.f32) < p_F:
                    h = _sample_hemisphere_ggx_h(t, b, n, alpha)
                    wi = _reflect(-wo, h)
                else:
                    wi = _sample_hemisphere_cosine_weighted(t, b, n)
                    h = (wi + wo).normalized()
                
                # 如果方向合法则评估
                if n.dot(wi) > 0:
                    cos_i = n.dot(wi)
                    cos_half = h.dot(wi)
                    ndoth = n.dot(h)
                    f_factor = _schlick_fresnel(cos_half)
                    
                    ## GGX 镜面项
                    D = _D_GGX(ndoth, alpha)
                    F = F0 + (1.0 - F0) * f_factor
                    G = _G_smith(cos_i, cos_o, alpha)
                    f_ggx = (D * F * G) / (4.0 * cos_i * cos_o)
                        
                    ## 漫反射项
                    Fd = Fd0 + (1.0 - Fd0) * f_factor
                    f_lambert = (1.0 - si.metallic) * (1 - Fd) * si.albedo / ti.math.pi
                    
                    f = f_ggx + f_lambert
                    
                    # 混合 PDF
                    pdf_ggx = D * ndoth / (4.0 * cos_half)
                    pdf_lambert = cos_i / ti.math.pi
                    pdf = p_F * pdf_ggx + p_T * pdf_lambert
                                        
                    bm = f * cos_i / pdf 
        else:
            # 均匀半球采样
            wi = _sample_hemisphere_uniform(t, b, n)
            f = PrincipledBSDF.f(wo, wi, si)
            bm = f * wi.dot(n) * (2.0 * ti.math.pi)
            pdf = 1.0 / (2.0 * ti.math.pi)
        
        # 确保在几何法线的上方
        if wi.dot(si.geo_normal) < 0:
            wi = _reflect(wi, si.geo_normal)
        
        return bm, wi, pdf

BSDF 计算部分较容易理解，即为把上面的公式用代码实现，较复杂的部分涉及到重要性采样，我们分析下：

1. GGX 重要性采样

我们希望根据 GGX 分布 $D(h)$ 来采样半程向量 $h$。常见方法是通过反演采样公式得到 $\theta_h$：

\[\theta_h = \arctan\left(\frac{\alpha \sqrt{\xi}}{\sqrt{1 - \xi}}\right), \quad \phi_h = 2\pi u\]

其中 $\alpha$ 是粗糙度，$\xi, u \in [0,1)$ 是均匀随机数。

得到 $h$ 后，再通过反射公式 $\omega_o = 2(\omega_i \cdot h)h - \omega_i$ 得到出射方向。

对应采样概率密度函数 (PDF) 为：

\[p(\boldsymbol{\omega}_o) = \frac{D(\boldsymbol{h})\ (\boldsymbol{n}\cdot \boldsymbol{h})}{4(\boldsymbol{\omega}_o \cdot \boldsymbol{h})}\]

2. 镜面与漫反射的混合采样

在电介质 PBR 材质中，光线通常既有漫反射成分，也有镜面反射成分。我们可以按一定比例在两者之间选择采样：

若随机数 $u < p_\text{spec}$，执行 GGX 重要性采样。
否则执行漫反射反射重要性采样，使用余弦加权半球面采样。

这个比例 $p_\text{spec}$ 取决于反射分量与漫反射（透射）分量的亮度之比，在上一篇文章的 BSDF 拓展阶段已经提到过。

这种设计使得采样方向和 BRDF 的分布尽可能匹配，从而大幅降低方差，加速收敛。

20.6 效果对比

首先我们比较下对 GGX BRDF 模型下的 PBR 物体渲染结果：

实验设置：

场景：DamagedHelmet

材质：PBR

每像素采样数：65536 spp

路径跟踪算法：随机游走

采样策略：均匀采样 vs. 重要性采样

对粗糙度较低的材质，均匀采样和重要性采样的差异尤其显著。均匀采样的大部分样本都落在没有贡献的方向，极低的采样效率造成了可见的瑕疵。

接下来再看下与 Blender Cycles 的参考渲染结果对比：

左：Blender Cycles 渲染结果 | 右：我们实现的基于 GGX BRDF 的 PBR 渲染结果

可以看到，我们的渲染结果与 Cycles 的参考渲染结果已经基本完全一致，只留下一些法线计算带来的差异。

21. 直接光源采样

在前面的路径追踪中，我们只依靠 BSDF 的重要性采样来决定光线的弹射方向。这种方法在处理大范围、均匀分布的照明时效果不错，但一旦场景中存在面积较小的光源，问题就会显现出来：光线随机弹射到光源的概率极低。换句话说，即使光源很亮，它的贡献也可能需要经过成百上千次采样才能被“撞中”。这就是常见的高噪声来源之一。

对于 DamagedHelmet 场景，我们的渲染器需要渲染 65536 样本，但还是有可见的噪声；与之对比，Blender Cycles 的渲染器只需要 128 样本就能得到非常好的结果。

从重要性采样的角度看，BSDF 的分布和光源分布通常差异很大。BSDF 倾向于沿反射方向分布，而光源却集中在特定小区域里。这样的错配导致我们虽然在 BSDF 的分布下做了重要性采样，但对光源贡献的估计依旧极不高效。

因此，我们需要引入 直接光源采样：在每个相交点，我们不再“等着”随机采样命中光源，而是显式地从光源分布中采样一个方向，直接估计它的贡献。这种做法通常被称为 Next Event Estimation (NEE)，意思是在每次相交事件发生后，我们立刻去估计“下一次事件”——也就是从当前点直接连向光源的能量交换。

21.1 分解渲染方程

我们先回顾完整的渲染方程：

\[L_o(\boldsymbol{p}, \boldsymbol{\omega}_o) = L_e(\boldsymbol{p}, \boldsymbol{\omega}_o) + \int_{\mathbb{S}^2} f_s(\boldsymbol{p}, \boldsymbol{\omega}_i, \boldsymbol{\omega}_o)\ L_i(\boldsymbol{p}, \boldsymbol{\omega}_i)\ |\boldsymbol{n}\cdot \boldsymbol{\omega}_i|\ d\boldsymbol{\omega}_i.\]

其中：

$L_e$ 表示表面点自身的发射辐亮度（如果 $\boldsymbol{p}$ 在光源上，这一项非零）。
$L_i$ 表示来自方向 $\boldsymbol{\omega}_i$ 的入射辐亮度。

为了更高效地处理，我们将 $L_i$ 拆分为两部分：

直接光照 (Direct Illumination) 来自场景光源的直接贡献，记作 $L_{\text{direct}}$。它只在光源可见的方向上为非零。
间接光照 (Indirect Illumination) 来自其他表面经过一次或多次反射/折射后到达 $\boldsymbol{p}$ 的辐亮度，记作 $L_{\text{indirect}}$。

于是渲染方程可改写为：

\[L_o(\boldsymbol{p}, \boldsymbol{\omega}_o) = L_e(\boldsymbol{p}, \boldsymbol{\omega}_o) + L_{\text{direct}}(\boldsymbol{p}, \boldsymbol{\omega}_o) + L_{\text{indirect}}(\boldsymbol{p}, \boldsymbol{\omega}_o).\]

具体来说：

直接光照项

\[L_{\text{direct}}(\boldsymbol{p}, \boldsymbol{\omega}_o) = \int_{\mathbb{S}^2} f_s(\boldsymbol{p}, \boldsymbol{\omega}_i, \boldsymbol{\omega}_o)\ L_i^{\text{direct}}(\boldsymbol{p}, \boldsymbol{\omega}_i)\ |\boldsymbol{n}\cdot \boldsymbol{\omega}_i|\ d\boldsymbol{\omega}_i\]

间接光照项

\[L_{\text{indirect}}(\boldsymbol{p}, \boldsymbol{\omega}_o) = \int_{\mathbb{S}^2} f_s(\boldsymbol{p}, \boldsymbol{\omega}_i, \boldsymbol{\omega}_o)\ (L_i(\boldsymbol{p}, \boldsymbol{\omega}_i) - L_i^{\text{direct}}(\boldsymbol{p}, \boldsymbol{\omega}_i))\ |\boldsymbol{n}\cdot \boldsymbol{\omega}_i|\ d\boldsymbol{\omega}_i\]

这样，直接光和间接光就被明确分离出来，便于分别处理：

直接光部分 可以通过 光源采样 (Next Event Estimation, NEE) 高效估计。
间接光部分 则依然由路径追踪（BSDF 采样）递归求解。

换句话说：NEE 负责“马上去看光源能贡献多少”，路径追踪负责“继续探索光线在场景中的反射和折射”。两者结合，才能既降低噪声，又保证全局光照的正确性。

21.2 光源面积积分

直接光照的积分形式最初写作球面角上的积分：

其中 $L_i^{\text{direct}}$ 只在光源方向非零，也就是说，真正有贡献的部分仅来自 光源对应的立体角区域。因此我们可以将积分范围缩小到该区域。但是在球面角空间中采样光源往往困难，因为我们很难直接控制哪些方向落在光源对应的角度范围内。在面积空间中采样则更自然，我们可以直接在光源表面 $A_l$ 上随机挑选一个点 $\boldsymbol{p}_l$，再连一条光线到 $\boldsymbol{p}$，计算贡献。

因此，我们把积分变量从方向 $\boldsymbol{\omega}_i$ 转换为光源表面上的面积点 $\boldsymbol{p}_l \in A_l$。两者的关系为：

\[d\omega_i = \frac{|\boldsymbol{n}_l \cdot (-\boldsymbol{\omega}_i)|}{\|\boldsymbol{p}_l - \boldsymbol{p}\|^2}\ dA_l,\]

其中 $\boldsymbol{n}_l$ 是光源点 $\boldsymbol{p}_l$ 的表面法线。代入后，我们得到面积积分形式：

\[L_{\text{direct}}(\boldsymbol{p}, \boldsymbol{\omega}_o) = \int_{A_l} f_s(\boldsymbol{p}, \boldsymbol{\omega}_i, \boldsymbol{\omega}_o)\ L_i^{\text{direct}}(\boldsymbol{p}, \boldsymbol{\omega}_i)\ \frac{(\boldsymbol{n}\cdot \boldsymbol{\omega}_i)\ (\boldsymbol{n}_l\cdot (-\boldsymbol{\omega}_i))}{\|\boldsymbol{p}_l - \boldsymbol{p}\|^2}\ dA_l.\]

在最后一步，我们将 $\boldsymbol{p}$ 点处的入射辐亮度改写为光源发出的辐亮度。需要注意的是，光源点 $\boldsymbol{p}_l$ 的发射辐亮度 $L_e$ 表示它“潜在的”贡献，但这束光线能否真正到达表面点 $\boldsymbol{p}$，还取决于中间是否有遮挡。为此，我们引入 可见性函数 $V(\boldsymbol{p}, \boldsymbol{p}_l)$：无遮挡时为 1，被遮挡时为 0。将其加入后，公式变为最终形式：

\[L_{\text{direct}}(\boldsymbol{p}, \boldsymbol{\omega}_o) = \int_{A_l} f_s(\boldsymbol{p}, \boldsymbol{\omega}_i, \boldsymbol{\omega}_o)\ L_e(\boldsymbol{p}_l, -\boldsymbol{\omega}_i)\ V(\boldsymbol{p}, \boldsymbol{p}_l)\ \frac{(\boldsymbol{n}\cdot \boldsymbol{\omega}_i)\ (\boldsymbol{n}_l\cdot (-\boldsymbol{\omega}_i))}{\|\boldsymbol{p}_l - \boldsymbol{p}\|^2}\ dA_l.\]

这就是 直接光源采样的核心公式。它说明一个光源点 $\boldsymbol{p}_l$ 对表面点 $\boldsymbol{p}$ 的贡献由以下几方面共同决定：

材质反射特性：由 BRDF $f_s$ 控制能量如何散射。
几何关系：两个余弦项描述了光源与表面的相对朝向。
空间衰减：距离平方项 $\|\boldsymbol{p}_l - \boldsymbol{p}\|^2$ 带来能量随距离衰减。
可见性：$V(\boldsymbol{p}, \boldsymbol{p}_l)$ 确保只有无遮挡的光源点才真正产生贡献。

直观来说,如果光源正对表面，且距离近并无遮挡，则贡献最大；如果光源倾斜、距离远，或中间被遮挡，则贡献会减小甚至为零。

这就是 Next Event Estimation (NEE) 的数学基础。通过把积分写成光源面积形式，我们能直接、显式地采样光源，而不是“等”光线随机击中。这样能显著降低小面积光源场景下的噪声。

21.3 光源功率采样

对于这个按光源表面点采样进行的蒙特卡罗积分，我们也可以使用重要性采样来减少方差，提高样本效率。

类比 BSDF 重要性采样，其在角度空间上进行，通过已知的 BRDF 分布来指导入射方向采样，权重大的部分提升采样概率，反之减少采样。

那么问题来了：在光源表面上，我们可以选用什么样的分布来指导采样？

如果我们直接对所有光源均匀采样，就会遇到和 BSDF 均匀采样类似的问题——某些亮度极高的光源很少被选中，从而导致噪声。更好的方法是根据光源的 相对能量贡献 来分配采样概率，这通常以光源的 功率 (power) 作为权重。

这就是 光源功率采样 (power sampling) 的思想：

首先计算场景中每个光源的功率（辐射总能量）；
然后根据功率构建一个概率分布函数；
在进行直接光源采样时，先按这个分布挑选一个光源，再在其表面上进行面积采样。

这样，亮度高、贡献大的光源更容易被选中，从而显著降低方差，提高采样效率。

21.4 代码实现

@ti.data_oriented
class NextEventEstimationPathIntegrator(PathIntegrator):
    def __init__(
        self,
        propagate_limit,
        BSDF_importance_sampling: bool = True,
    ):
        self.propagate_limit = propagate_limit
        self.BSDF_importance_sampling = BSDF_importance_sampling
        self.lights_pdf = None
        
    def prepare(self, world):
        # 构建光源分布的 AliasTable，用于重要性采样光源
        lights_power = [
            world.lights_BVH.primitives[i].power()
            for i in range(world.lights_BVH.primitive_cnt[None])
        ]
        self.lights_pdf = AliasTable(len(lights_power))
        self.lights_pdf.build(np.array(lights_power, dtype=np.float32))
        
    @ti.func
    def run(self, ray: ti.template(), world: ti.template()):
        bounce = 0
        l = Vec3f(0.0)     # 累积辐亮度
        beta = Vec3f(1.0)  # 路径权重
        
        while True:
            # 1. 光线与场景相交
            record = world.hit(ray)
            
            # 2. 若未命中任何物体，则返回环境光并终止
            if record.prim_type == PrimitiveType.UNHIT:
                l += beta * world.env.sample(ray.rd)
                break
                
            # 3. 加上表面自发光
            # 注意：如果第一跳就直接打到光源，可以记录自发光；
            # 后续 bounce 打到光源时，不再重复累加（避免 double-counting）
            if bounce == 0 or record.prim_type != PrimitiveType.LIGHT:
                l += beta * record.si.emission
            
            # 4. 路径长度达到上限，终止
            bounce += 1
            if bounce >= self.propagate_limit:
                break
        
            # 5. Next Event Estimation (直接光源采样)
            # 5.1 按照光源功率分布选择一个光源
            light_id, prob = self.lights_pdf.sample()
            light = world.lights_BVH.primitives[light_id]
            
            # 5.2 在该光源表面采样一个点，生成 shadow ray
            light_pos, light_normal = light.sample()
            light_dir = light_pos - record.si.point
            distance = light_dir.norm()
            light_dir /= distance
            shadow_ray = Ray(ro=record.si.point, rd=light_dir)
            
            # 5.3 计算几何项的余弦
            cos_lo = -light_normal.dot(light_dir)     # 光源面法线与出射方向夹角
            cos_li = record.si.normal.dot(light_dir)  # 表面法线与入射方向夹角
            
            # 5.4 如果两边朝向都正确，则进行可见性测试
            if cos_lo > 0 and cos_li > 0:
                shadow_record = world.shadow_hit(shadow_ray)
                
                # 如果 shadow ray 确实击中同一个光源点，且距离一致 → 可见
                if (
                    shadow_record.prim_type == PrimitiveType.LIGHT
                    and shadow_record.prim_id == light_id
                    and abs(shadow_record.t - distance) < 1e-4
                ):
                    # 光源采样的 pdf（面积域 → 方向域转换）
                    light_pdf = prob * (distance * distance) / (cos_lo * light.area())
                    
                    # BSDF 在当前方向下的值
                    f = PrincipledBSDF.f(-ray.rd, light_dir, record.si)
                    
                    # 累积直接光照
                    l += beta * cos_li * f * light.radiance / light_pdf
                    
            # 6. BSDF 采样一个新方向，继续路径追踪（间接光照部分）
            bm, wi, pdf = PrincipledBSDF.sample(
                -ray.rd, record.si,
                use_importance_sampling=self.BSDF_importance_sampling
            )
            ray.ro = record.si.point
            ray.rd = wi
            beta *= bm
                
            # 7. 如果权重衰减到近似零，提前终止
            if beta[0] < 1e-8 and beta[1] < 1e-8 and beta[2] < 1e-8:
                break
                
        return l

这里有几个值得注意的地方：

1. 别名采样（Alias Sampling）

在第 5 步中，我们通过 AliasTable 来按光源功率进行重要性采样。这种方法基于 Alias Method（别名采样），可以在 $O(1)$ 的时间内从任意非均匀分布中采样出离散事件。

它的核心思想是：先将每个光源的概率归一化，然后构建一张表，把每个采样桶补充到等概率区间，再为多余部分建立“别名”索引。采样时，我们只需生成两个随机数：一个用于选桶，另一个决定是使用原桶还是别名桶。

这种方法的优点是：

构建开销仅 $O(n)$；
查询时恒为 $O(1)$；
能显著提升多光源场景的采样效率。

参考阅读：时间复杂度为O(1)的抽样算法——别名采样（alias sample）

2. 光源自发光的处理与 NEE 渲染方程展开

引入 Next Event Estimation（NEE）之后，渲染方程的展开也发生了变化。

其中光源贡献 $L_{\text{direct}}$ 由 21.2 节的推导，转化为了对光源自发光 $L_e$ 的积分，因此不再需要递归展开。

而间接光照项 $L_{\text{indirect}}$ 则需要递归展开，递归计算所有入射方向的辐亮度，其公式为

其中我们显式减去了直接光项 $L_i^{\text{direct}}$，因为这部分已经通过 NEE 单独采样得到了。

这正是代码中以下条件判断的原因：

if bounce == 0 or record.prim_type != PrimitiveType.LIGHT:
    l += beta * record.si.emission

第一次击中光源（即路径起点直接命中）时，应累加 $L_e$，对应于第一次展开渲染方程。
后续弹射若命中光源，则该光源已在 NEE 中被显式采样过，因此不再累加。

这保证了理论上的一致性： 光源直接项通过 NEE 计算，间接项通过递归展开，二者不重叠。

21.5 效果对比

实验设置：

场景：Cornell Box

材质：漫反射

每像素采样数：128 spp

路径跟踪算法：随机游走 vs. 直接光源采样

从图中可以看到，直接光源采样算法显著减少了噪声，在小采样数下也能获得较好的结果。

22. 多重重要性采样

上面的直接光源采样算法虽然能考虑光源的重要性，但并不是完美的。下面我们来看一个包含不同粗糙度反射表面的测试场景。

使用 直接光源采样，我们得到：

对于 较低粗糙度（接近镜面） 且 光源较大 的区域，可以看到明显的噪点和伪影。这是因为光源采样的方向分布与镜面反射的能量分布差异很大，导致大多数样本几乎没有贡献。

相反，如果我们直接使用最开始的 基于 BSDF 重要性采样 的随机游走追踪器（即不进行显式光源采样），则得到：

这次表现刚好相反：低粗糙度材质 上的结果比较平滑，但对于 高粗糙度材质 或者 小光源，因为 BSDF 采样很难命中光源，反而出现严重噪声。

换句话说：

光源采样 对小粗糙度、宽反射区无能为力；
BSDF 采样 对尖锐高光、小面积光源效率极低。

这两个方法在不同区域各有优势与盲点—— 于是，自然的想法是：能不能让它们协作起来？让每个采样方法在自己擅长的场景中贡献更大，而在不擅长时自动降低权重。

这正是我们接下来要介绍的 —— 多重重要性采样（Multiple Importance Sampling, MIS）。

22.1 原理

在上文中，我们看到两种方法的各自局限：直接光源采样在镜面区域容易产生噪点，而 BSDF 采样在小光源场景中难以收敛。

实际上，这两者本质上是在估计 同一个积分项 —— 渲染方程中 直接光照部分的积分，只是采用了 不同的采样分布：

NEE（光源采样）：按照光源辐射功率的分布采样方向；
BSDF 采样：按照材质反射分布采样方向。

换句话说，它们并不是在做两件不同的事，而是用 两种重要性采样策略 来近似同一个积分。

因此，我们完全可以把两种结果都计算一遍，然后再用合适的权重合并，既利用光源分布的信息，又利用材质分布的信息，从而在所有场景下都获得更低的方差。

这正是 多重重要性采样（Multiple Importance Sampling, MIS） 的核心思想：

对同一积分的多个采样分布结果，进行加权融合，以最小化总体方差。

22.2 启发式与权重公式

假设我们对同一个积分项进行了两种采样：

来自 光源采样分布 的样本 $\omega^l$，概率密度为 $p_l(\omega)$；
来自 BSDF 采样分布 的样本 $\omega^b$，概率密度为 $p_b(\omega)$。

那么，一个自然的融合方式是对两者都进行蒙特卡罗估计，并以权重 $w_l$ 与 $w_b$ 进行加权平均：

\[L_{\text{direct}} \approx \frac{1}{N_l} \sum_{i=1}^{N_l} w_l(\omega^l_i)\ \frac{f(\omega^l_i)}{p_l(\omega^l_i)} + \frac{1}{N_b} \sum_{j=1}^{N_b} w_b(\omega^b_j)\ \frac{f(\omega^b_j)}{p_b(\omega^b_j)}.\]

其中 $w_l(\omega)$ 与 $w_b(\omega)$ 满足 $w_l + w_b = 1$。

为了让两种采样方法“合作”，我们需要决定——在每个采样方向上，该信任哪种方法更多，即决定如何分配权重。

平衡启发式（Balance Heuristic）

最常用的一种权重计算方式是 平衡启发式（balance heuristic）：

\[w_l(\omega) = \frac{p_l(\omega)}{p_l(\omega) + p_b(\omega)}, \qquad w_b(\omega) = \frac{p_b(\omega)}{p_l(\omega) + p_b(\omega)}.\]

它的意义非常直观：如果一个方向在光源采样中概率较高（容易采到），则信任光源采样的估计更多；反之，如果该方向在 BSDF 采样中更容易采到，则由 BSDF 采样主导。

这种启发式保证了在两种分布相近时，两种样本贡献接近均衡；而在任一分布概率极小的区域，能自动降低其噪声影响。

幂次启发式（Power Heuristic）

在实践中，为了让权重对概率差异更加敏感，通常使用 幂次启发式（power heuristic），即在平衡启发式中引入指数 $\beta$（常取 2）：

\[w_l(\omega) = \frac{[p_l(\omega)]^\beta}{[p_l(\omega)]^\beta + [p_b(\omega)]^\beta}, \qquad w_b(\omega) = \frac{[p_b(\omega)]^\beta}{[p_l(\omega)]^\beta + [p_b(\omega)]^\beta}.\]

当 $\beta = 2$ 时，这种方式通常能获得更低的方差，也是现代路径追踪器的默认选择。

22.3 代码实现

@ti.data_oriented
class NextEventEstimationPathIntegrator(PathIntegrator):
    def __init__(
        self,
        propagate_limit,
        BSDF_importance_sampling: bool = True,
        nee_multi_importance_sampling: bool = True,
    ):
        self.propagate_limit = propagate_limit
        self.BSDF_importance_sampling = BSDF_importance_sampling
        self.nee_multi_importance_sampling = nee_multi_importance_sampling
        self.lights_pdf = None
        
    def prepare(self, world):
        # 构建光源分布的 AliasTable，用于重要性采样光源
        lights_power = [
            world.lights_BVH.primitives[i].power()
            for i in range(world.lights_BVH.primitive_cnt[None])
        ]
        self.lights_pdf = AliasTable(len(lights_power))
        self.lights_pdf.build(np.array(lights_power, dtype=np.float32))
        
    @ti.func
    def run(self, ray: ti.template(), world: ti.template()):
        bounce = 0
        l = Vec3f(0.0)     # 累积辐亮度
        beta = Vec3f(1.0)  # 路径权重
        pdf = 0.0          # 上一跳的 BSDF 采样概率，用于 MIS 计算
        
        while True:
            # 1. 光线与场景相交
            record = world.hit(ray)
            
            # 2. 若未命中任何物体，则返回环境光并终止
            if record.prim_type == PrimitiveType.UNHIT:
                l += beta * world.env.sample(ray.rd)
                break
                
            # 3. 处理光源自发光
            # 若为第一次 bounce 或者命中的不是光源 → 直接累加自发光
            if bounce == 0 or record.prim_type != PrimitiveType.LIGHT:
                l += beta * record.si.emission
                
            # 若启用 MIS，则命中光源时需考虑 BSDF 与光源采样的双重分布
            elif self.nee_multi_importance_sampling:
                mis_weight = 1.0
                if not ti.math.isinf(pdf):  # pdf=inf 表示镜面反射，直接使用 BSDF 采样
                    prob = self.lights_pdf.probs[record.prim_id]
                    light = world.lights_BVH.primitives[record.prim_id]
                    cos_lo = -record.si.normal.dot(ray.rd)
                    light_pdf = prob * (record.t * record.t) / (cos_lo * light.area())
                    light_pdf2 = light_pdf * light_pdf
                    pdf2 = pdf * pdf
                    mis_weight = pdf2 / (pdf2 + light_pdf2)
                l += beta * mis_weight * record.si.emission
            
            # 4. 路径长度达到上限，终止
            bounce += 1
            if bounce >= self.propagate_limit:
                break
        
            # 5. Next Event Estimation (直接光源采样)
            # 5.1 按功率分布采样一个光源
            light_id, prob = self.lights_pdf.sample()
            light = world.lights_BVH.primitives[light_id]
            
            # 5.2 在光源表面采样一个点，生成 shadow ray
            light_pos, light_normal = light.sample()
            light_dir = light_pos - record.si.point
            distance = light_dir.norm()
            light_dir /= distance
            shadow_ray = Ray(ro=record.si.point, rd=light_dir)
            
            # 5.3 计算几何项余弦
            cos_lo = -light_normal.dot(light_dir)
            cos_li = record.si.normal.dot(light_dir)
            
            # 5.4 若两面朝向都正确，则进行可见性测试
            if cos_lo > 0 and cos_li > 0:
                shadow_record = world.shadow_hit(shadow_ray)
                if (
                    shadow_record.prim_type == PrimitiveType.LIGHT
                    and shadow_record.prim_id == light_id
                    and abs(shadow_record.t - distance) < 1e-4
                ):
                    # 面积域 → 方向域的 pdf 转换
                    light_pdf = prob * (distance * distance) / (cos_lo * light.area())
                    
                    # 当前入射方向下的 BSDF 值
                    f = PrincipledBSDF.f(-ray.rd, light_dir, record.si)
                    
                    # MIS 权重计算
                    mis_weight = 1.0
                    if self.nee_multi_importance_sampling:
                        pdf = PrincipledBSDF.pdf(
                            -ray.rd, light_dir, record.si,
                            use_importance_sampling=self.BSDF_importance_sampling
                        )
                        light_pdf2 = light_pdf * light_pdf
                        pdf2 = pdf * pdf
                        mis_weight = light_pdf2 / (pdf2 + light_pdf2)
                    
                    # 累加直接光贡献
                    l += beta * mis_weight * cos_li * f * light.radiance / light_pdf
                    
            # 6. BSDF 采样下一个方向，继续追踪（间接光照）
            bm, wi, pdf = PrincipledBSDF.sample(
                -ray.rd, record.si,
                use_importance_sampling=self.BSDF_importance_sampling
            )
            ray.ro = record.si.point
            ray.rd = wi
            beta *= bm
                
            # 7. 若路径权重衰减至近零，则终止
            if beta[0] < 1e-8 and beta[1] < 1e-8 and beta[2] < 1e-8:
                break
                
        return l

对于代码中的关键点，这里详细说明如下。

1. 多重重要性采样

权重采用 幂次启发式（$\beta=2$）：

在代码中，通过 light_pdf2 / (pdf2 + light_pdf2) 实现该公式。

2. 光源命中时的 MIS 权重

当路径反弹后直接命中光源时（例如镜面反射击中光源），这次命中可被视为一次 BSDF 采样结果。若不加修正，会与前面的 NEE 重复计算。

因此在第 3 步中：

elif self.nee_multi_importance_sampling:
    ...
    mis_weight = pdf2 / (pdf2 + light_pdf2)
    l += beta * mis_weight * record.si.emission

这里权重采用对称形式，使得两种路径（光源采样与 BSDF 采样）对同一贡献只被部分计入。

与上一节（仅 NEE）的实现相比，主要区别在两处：

步骤	NEE-only 实现	NEE + MIS 实现
光源命中时	跳过（$w_b=0$）	考虑 MIS（$w_b=p_b^2/(p_b^2+p_l^2)$）
阴影光线采样	直接累加（$w_l=1$）	考虑 MIS（$w_l=p_l^2/(p_b^2+p_l^2)$）

这样在能量估计上更加平衡，尤其是对细长或高亮光源和低粗糙度的半镜面材质。这些情况下 MIS 能显著降低噪点，提高收敛速度。

22.4 效果对比

实验设置：

场景：Reflective Bars

材质：不同粗糙度的金属

每像素采样数：1024 spp

路径跟踪算法：直接光源采样 vs. 多重重要性采样

从图中可以看到，多重重要性采样方法结合了光源采样和 BSDF 采样的双重分布，能有效降低噪声，提高收敛速度。

23. 环境光重要性采样

在上一节我们讨论了多重重要性采样（MIS）如何在直接光估计中有效结合光源采样与 BSDF 采样，从而降低方差。而在路径追踪中，除了局部光源，环境光（Environment Light） 也是一个关键的能量来源，特别是在只有 HDR 环境贴图而无显式光源的场景中。然而，环境光并非一个离散的光源集合，而是定义在整个单位球面上的连续辐射场，这使得它的采样策略与常规光源不同。

23.1 按亮度加权的采样

对于环境光，入射直接光辐亮度 $L_i^{\text{direct}}(\boldsymbol{p}, \boldsymbol{\omega}_i)$ 并非来自某个几何光源，而是由环境贴图定义的方向函数 $L_\text{env}(\boldsymbol{\omega}_i)$。

因此我们要在球面上对方向进行采样。若直接在单位球面上均匀采样方向，虽然实现简单，但由于环境贴图中亮度分布往往高度不均匀（例如太阳或高亮区域），会导致严重的噪声。

为了减少方差，我们希望按环境贴图的亮度分布进行重要性采样，即采样概率 $p(\omega)$ 与$L_\text{env}(\omega)$ 成正比：

\[p(\omega) \propto L_\text{env}(\omega)\]

然而，环境贴图通常是以经纬度展开的 2D 图像 $L_\text{env}(u,v)$，需要考虑球面坐标变换的面积权重。由于每个纬度带对应球面上的面积比例 $\sin\theta$，最终正确的采样概率应为：

\[p(u,v) \propto L_\text{env}(u,v) \sin\theta\]

因此在构建采样表时，应同时考虑像素亮度与纬度权重。

23.2 代码实现

@ti.data_oriented
class NextEventEstimationPathIntegrator(PathIntegrator):
    def __init__(
        self,
        propagate_limit,
        BSDF_importance_sampling: bool = True,
        nee_multi_importance_sampling: bool = True,
        envmap_importance_sampling: bool = True,
    ):
        self.propagate_limit = propagate_limit
        self.BSDF_importance_sampling = BSDF_importance_sampling
        self.nee_multi_importance_sampling = nee_multi_importance_sampling
        self.envmap_importance_sampling = envmap_importance_sampling

        # 光源相关
        self.has_light = False
        self.lights_pdf = AliasTable(1)

        # 环境光相关
        self.env_support_is = False                     # 场景是否有 ImageEnvironment
        self.envmap_pdf = AliasTable(1)                # envmap 的重要性采样分布
        self.envmap_width = 1024
        self.envmap_height = 1024
        self.envmap_id = 0

    def prepare(self, world, ref_point=Vec3f(0.0)):
        # 1. 构建光源重要性采样 AliasTable
        self.has_light = world.lights_BVH.primitive_cnt[None] > 0
        if self.has_light:
            lights_power = [
                world.lights_BVH.primitives[i].power()
                for i in range(world.lights_BVH.primitive_cnt[None])
            ]
            self.lights_pdf = AliasTable(len(lights_power))
            self.lights_pdf.build(np.array(lights_power, dtype=np.float32))

        # 2. 构建环境光重要性采样 AliasTable（仅支持 ImageEnvironment）
        self.env_support_is = isinstance(world.env, ImageEnvironment)
        if self.envmap_importance_sampling and self.env_support_is:
            envmap = world.env.map.to_numpy()
            self.envmap_width = envmap.shape[0]
            self.envmap_height = envmap.shape[1]

            # 2.1 计算每个像素的亮度（Y = 0.2126 R + 0.7152 G + 0.0722 B）
            envmap_lum = 0.2126*envmap[:,:,0] + 0.7152*envmap[:,:,1] + 0.0722*envmap[:,:,2]

            # 2.2 构建像素索引网格
            uv = np.mgrid[0:envmap.shape[0], 0:envmap.shape[1]].astype(np.float32)
            u = (uv[0] + 0.5) / envmap.shape[0]
            v = (uv[1] + 0.5) / envmap.shape[1]

            # 2.3 修正球面映射的 Jacobian
            jacobian = 0.5 * np.pi * np.sin(np.pi * v)
            envmap_lum *= jacobian

            # 2.4 构建 envmap AliasTable
            self.envmap_pdf = AliasTable(envmap.shape[0] * envmap.shape[1])
            self.envmap_pdf.build(envmap_lum.reshape(-1))

    @ti.func
    def run(self, ray: ti.template(), world: ti.template()):
        bounce = 0
        l = Vec3f(0.0)        # 累积辐亮度
        beta = Vec3f(1.0)     # 路径权重
        pdf = 0.0             # 上一跳 BSDF pdf
        envmap_is = self.envmap_importance_sampling and self.env_support_is

        while True:
            # 1. 光线与场景相交
            record = world.hit(ray)

            # 2. 环境光采样
            if record.prim_type == PrimitiveType.UNHIT:
                # 2.1 若为第一次 bounce 或未启用 envmap 重要性采样 → 直接累加环境光
                if bounce == 0 or not envmap_is:
                    l += beta * world.env.sample(ray.rd)

                # 2.2 启用 MIS 进行多重重要性采样
                elif self.nee_multi_importance_sampling:
                    mis_weight = 1.0
                    if not ti.math.isinf(pdf):  # pdf=inf 表示镜面反射，仅使用 BSDF
                        # 将方向转为 envmap 像素索引
                        u = (ti.math.atan2(ray.rd[2], ray.rd[0]) / (2.0 * ti.math.pi) + 0.5) * self.envmap_width
                        v = (ti.math.asin(ti.math.clamp(ray.rd[1], -1, 1)) / ti.math.pi + 0.5) * self.envmap_height
                        pix_id = int(u) * self.envmap_height + int(v)

                        # 获取 envmap PDF
                        prob = self.envmap_pdf.probs[pix_id]

                        # 面积域 → 方向域转换
                        cos_theta = ti.math.sqrt(ray.rd[0] * ray.rd[0] + ray.rd[2] * ray.rd[2])
                        light_pdf = prob * (self.envmap_width * self.envmap_height) / (2 * ti.math.pi * ti.math.pi * cos_theta)

                        # MIS 权重
                        light_pdf2 = light_pdf * light_pdf
                        pdf2 = pdf * pdf
                        mis_weight = pdf2 / (pdf2 + light_pdf2)

                    # 累加环境光
                    l += beta * mis_weight * world.env.sample(ray.rd)

                break

            # 3. 光源自发光累加
            if bounce == 0 or record.prim_type != PrimitiveType.LIGHT:
                l += beta * record.si.emission
            elif self.nee_multi_importance_sampling:
                mis_weight = 1.0
                if not ti.math.isinf(pdf):
                    prob = self.lights_pdf.probs[record.prim_id]
                    light = world.lights_BVH.primitives[record.prim_id]
                    cos_lo = -record.si.normal.dot(ray.rd)
                    light_pdf = prob * (record.t * record.t) / (cos_lo * light.area())
                    light_pdf2 = light_pdf * light_pdf
                    pdf2 = pdf * pdf
                    mis_weight = pdf2 / (pdf2 + light_pdf2)
                l += beta * mis_weight * record.si.emission

            # 4. 路径长度限制
            bounce += 1
            if bounce >= self.propagate_limit:
                break

            # 5. 光源直接光采样（Next Event Estimation）
            light_id, prob = self.lights_pdf.sample()
            light = world.lights_BVH.primitives[light_id]
            light_pos, light_normal = light.sample()
            light_dir = light_pos - record.si.point
            distance = light_dir.norm()
            light_dir /= distance
            shadow_ray = Ray(ro=record.si.point, rd=light_dir)
            cos_lo = -light_normal.dot(light_dir)
            cos_li = record.si.normal.dot(light_dir)

            if cos_lo > 0 and cos_li > 0:
                shadow_record = world.shadow_hit(shadow_ray)
                if shadow_record.prim_type == PrimitiveType.LIGHT and shadow_record.prim_id == light_id and abs(shadow_record.t - distance) < 1e-4:
                    light_pdf = prob * (distance * distance) / (cos_lo * light.area())
                    f = PrincipledBSDF.f(-ray.rd, light_dir, record.si)
                    mis_weight = 1.0
                    if self.nee_multi_importance_sampling:
                        pdf = PrincipledBSDF.pdf(-ray.rd, light_dir, record.si, use_importance_sampling=self.BSDF_importance_sampling)
                        light_pdf2 = light_pdf * light_pdf
                        pdf2 = pdf * pdf
                        mis_weight = light_pdf2 / (pdf2 + light_pdf2)
                    l += beta * mis_weight * cos_li * f * light.radiance / light_pdf

            # 6. 环境光直接光采样（Next Event Estimation）
            if envmap_is:
                # 6.1 按 envmap PDF 采样像素
                pix_id, prob = self.envmap_pdf.sample()
                u = pix_id // self.envmap_height
                v = pix_id % self.envmap_height
                u_norm = (u + ti.random()) / self.envmap_width
                v_norm = (v + ti.random()) / self.envmap_height

                # 6.2 将像素坐标映射到球面方向
                phi = (u_norm - 0.5) * 2 * ti.math.pi
                theta = (v_norm - 0.5) * ti.math.pi
                cos_theta = ti.math.cos(theta)
                light_dir = Vec3f(
                    cos_theta * ti.math.cos(phi),
                    ti.math.sin(theta),
                    cos_theta * ti.math.sin(phi),
                )
                shadow_ray = Ray(ro=record.si.point, rd=light_dir)
                cos_li = record.si.normal.dot(light_dir)

                # 6.3 可见性测试
                if cos_li > 0:
                    shadow_record = world.shadow_hit(shadow_ray)
                    if shadow_record.prim_type == PrimitiveType.UNHIT:
                        # 6.4 面积域 → 方向域 pdf 转换
                        light_pdf = prob * (self.envmap_width * self.envmap_height) / (2 * ti.math.pi * ti.math.pi * cos_theta)
                        light_radiance = world.env.sample(light_dir)

                        # 6.5 BSDF 与 MIS
                        f = PrincipledBSDF.f(-ray.rd, light_dir, record.si)
                        mis_weight = 1.0
                        if self.nee_multi_importance_sampling:
                            pdf = PrincipledBSDF.pdf(-ray.rd, light_dir, record.si, use_importance_sampling=self.BSDF_importance_sampling)
                            light_pdf2 = light_pdf * light_pdf
                            pdf2 = pdf * pdf
                            mis_weight = light_pdf2 / (pdf2 + light_pdf2)

                        # 6.6 累加环境光直接光贡献
                        l += beta * mis_weight * cos_li * f * light_radiance / light_pdf

            # 7. BSDF 采样生成下一条路径
            bm, wi, pdf = PrincipledBSDF.sample(-ray.rd, record.si, use_importance_sampling=self.BSDF_importance_sampling)
            ray.ro = record.si.point
            ray.rd = wi
            beta *= bm

            # 8. 路径权重衰减至零，终止
            if beta[0] < 1e-8 and beta[1] < 1e-8 and beta[2] < 1e-8:
                break

        return l

在上面的实现中，环境光的重要性采样主要体现在 prepare() 和 run() 两个阶段：

1. 构建环境光采样表

envmap_lum = 0.2126*envmap[:,:,0] + 0.7152*envmap[:,:,1] + 0.0722*envmap[:,:,2]
jacobian = 0.5 * np.pi * np.sin(np.pi * v)
envmap_lum *= jacobian
self.envmap_pdf.build(envmap_lum.reshape(-1))

亮度加权：使用线性亮度 Y = 0.2126 R + 0.7152 G + 0.0722 B 作为每个像素的初始权重，反映该方向的能量大小。
纬度修正：乘以 $\sin\theta$（jacobian），保证采样概率与球面面积成正比，否则高纬度像素会被高估。
Alias Table 构建：将 2D 图像展平成 1D，并建立快速采样数据结构，实现 O(1) 的方向采样。

2. 直接环境光采样

pix_id, prob = self.envmap_pdf.sample()
...
light_dir = Vec3f(
    cos_theta * cos(phi),
    sin(theta),
    cos_theta * sin(phi),
)

根据重要性采样像素：按亮度 + Jacobian 采样出一个像素 pix_id，保证高亮区域被优先选择。
转换为球面方向：将 (u,v) 映射到球面坐标 (theta, phi)，再转换为三维方向向量 light_dir。
可见性测试：通过 shadow ray 判断该方向是否被场景遮挡，确保采样贡献有效。
BSDF 与 MIS 权重：计算对应 BSDF 值，并与采样概率做多重重要性加权，减少高亮方向噪声。

3. 环境光采样 PDF

在启用 MIS（Multiple Importance Sampling）时，需要计算环境光采样得到方向的 PDF，并与 BSDF 采样的方向 PDF 一起用于计算 MIS 权重。

假设通过 Alias Table 采样到环境贴图像素 (u,v)，Alias Table 返回该像素的离散概率 $p_\text{pix}$。

环境贴图是经纬度二维网格，宽度为 W，高度为 H。要将像素概率转换为单位球面方向的 PDF，需要考虑纬度的面积修正。

对经纬贴图（latitude–longitude）：

$\phi\in[0,2\pi)$（经度），像素宽方向的步长约为 $\Delta\phi = \tfrac{2\pi}{W}$；
纬度用 $\theta\in[-\tfrac{\pi}{2},\tfrac{\pi}{2}]$（latitude），像素高方向的步长约为 $\Delta\lambda = \tfrac{\pi}{H}$；
单位球面元：$\text d\omega = \cos\theta\ \text d\theta\ \text d\phi$。

因此每个像素的大致立体角为

\[\Delta\omega \approx \Delta\phi,\Delta\theta,\cos\theta = \frac{2\pi}{W}\cdot\frac{\pi}{H}\cdot\cos\theta = \frac{2\pi^2}{W H}\cos\theta.\]

如果 Alias 表返回该像素的离散概率 $p_\text{pix}$（所有像素之和为 1），要把它转成以单位立体角为衡量的方向 PDF：

\[p_\text{env}(\omega) = \frac{p_\text{pix}}{\Delta\omega} = p_\text{pix}\cdot\frac{W H}{2\pi^2\ \cos\theta}.\]

23.3 效果对比

实验设置：

场景：Reflective Bars

材质：不同粗糙度的金属

每像素采样数：1024 spp

路径跟踪算法：直接光源采样 + 多重重要性采样

采样策略：环境光随机采样 vs. 重要性采样

实验设置：

场景：DamagedHelmet

材质：PBR

每像素采样数：128 spp

路径跟踪算法：直接光源采样 + 多重重要性采样

采样策略：环境光随机采样 vs. 重要性采样

从上面的实验结果可以看出，环境光重要性采样可以有效地减少噪声，提升渲染效果。在 DamagedHelmet 场景中，我们初步赶上了 Blender Cycles 的采样效率。

24. 光源层次结构

在前面的章节中，我们介绍了直接光源采样（Next Event Estimation, NEE）。通过在每个相交点显式地采样光源，NEE 能显著提升少量光源场景下的收敛效率。

然而，当场景中存在数量庞大的光源（例如数百上千个小灯泡，或高分辨率的发光网格）时，问题又浮现出来。

设想这样一个场景：一个房间中分布着上千盏灯，但相机所在的角落实际上只被其中几盏灯照亮。如果我们仍然在所有光源上均匀采样或按总功率加权采样，那么大量样本都会浪费在那些距离很远的、几乎没有贡献的光源上。

理想的做法是：

采样概率应与光源对当前点的潜在贡献成正比。

换句话说，距离更近、朝向更合适、亮度更高的光源，应该更容易被采样到。此时，仅凭光源的总功率已经不足以衡量其真实贡献，我们还需要考虑光源与查询点之间的空间和几何关系。

为了解决这一问题，我们需要引入光源层次结构（Light Bounding Volume Hierarchy，LightBVH）。

LightBVH 通过对大量光源进行空间聚合与能量近似，使我们能够在采样阶段根据光源对当前点的潜在贡献分布进行高效的重要性采样，从而在大规模光源场景中显著提升渲染效率。

24.1 基本结构

LightBVH 的结构与传统的 BVH 十分类似，但它的目标不同。普通 BVH 主要用于加速光线与几何体的求交，而 LightBVH 则用于加速光源采样。

每个节点通常包含以下信息：

包围盒 (AABB)：记录该节点下所有光源的空间范围；
光源能量 (Power)：存储该节点下所有光源的总辐射功率；
层次结构信息 (Parent / Left / Right)：用于在采样或查询时自顶向下遍历。

一个典型的节点结构可以定义为：

LightBVHNode = ti.types.struct(
    parent=ti.i32,
    left=ti.i32,
    right=ti.i32,
    aabb=AABB,
    data=ti.i32,
    power=ti.f32
)

需要注意的是，与几何 BVH不同，LightBVH 并不需要执行光线求交遍历，因此不必维护类似 next 的辅助指针。但在采样阶段，我们常常需要从叶子节点回溯到根节点以计算重要性或采样概率，因此额外存储 parent 指针是必要的。

24.2 表面积功率启发式

在构建 LightBVH 时，我们希望每个节点都能尽可能准确地近似其包含光源对场景中任意点的潜在照明贡献。换句话说，划分的目标是最小化由节点近似带来的光源贡献估计误差。

从光照估计的角度看，节点代表了一组光源的近似贡献。当我们用一个包围盒来概括多个光源时，实际误差主要来源于两个方面：

空间误差：包围盒越大，光源实际分布与包围体近似之间的偏差越大；
能量权重：节点的能量越高，该近似误差对最终渲染结果的影响越明显。

因此，为了衡量划分的优劣，可以使用这样一个代价函数：

\[C = E_L \cdot S_L + E_R \cdot S_R\]

称为表面积功率启发式。其中 $E_L$ 和 $E_R$ 分别表示左右子节点的总辐射功率，$S_L$ 和 $S_R$ 分别表示左右子节点的包围盒表面积。

这个代价函数反映了上述两种误差来源: 来自于节点包围盒的空间误差，同时正比于节点功率，$E \cdot S$ 可以理解为“误差的大小 × 误差的重要性”的结合量。

从直观上看，这个启发式拥有两方面的效果：

其中之一是：鼓励空间上相近的光源聚合在一起。如果两个光源距离较近，它们合并后包围盒面积 $S$ 增加不多，总代价上升有限，因此倾向于被合并成一个节点。反之，如果光源相距很远或分布分散，合并后包围盒显著增大，导致 $E \cdot S$ 增加明显，构建过程会倾向于将它们分开。

另一个一个关键效果是：能量大的节点会被更精确地近似。由于高能量节点对整体光照估计的影响更大，构建算法会自动倾向于为这些光源簇保留更紧凑的包围盒。而能量较小的节点即使包围范围较大，也不会显著影响全局误差。结果是，LightBVH 自然形成了一种能量加权的层次结构：高能量区域划分更细，低能量区域划分更粗。

与传统几何 BVH 的表面积启发式（Surface Area Heuristic）相比：

启发式类型	优化目标	代价函数	含义
表面积启发式	最小化光线求交代价	$C_{trav} + \frac{S_L}{S_P} N_L C_{isect} + \frac{S_R}{S_P} N_R C_{isect}$	光线访问代价
表面积功率启发式	最小化光照估计误差	$E_L \cdot S_L + E_R \cdot S_R $	光源能量 × 空间误差

借助这种构建启发式，LightBVH 能在多光源场景中以更合理的层次聚合方式组织光源，使采样更集中于真正有贡献的区域，大幅提升全局照明的收敛效率。

简单修改 BVH 的代码，即可实现 LightBVH 的构建：

@ti.data_oriented
class LightBVH:
    def __init__(self, size):
        size = max(size, 16)
        self.nodes = LightBVHNode.field(shape=(2 * size - 1,))  # 所有节点
        self.id2node = ti.field(ti.i32, shape=(size))           # 光源 ID 到节点索引的映射
        self.node_cnt = ti.field(ti.i32, shape=())              # 已构建节点总数
        self.depth = 0                                          # BVH 最大深度

    # 节点划分函数：根据表面积功率启发式 (E × A) 找到最优划分方式
    @staticmethod
    def split_node(aabbs, centers, powers):
        min_cost = INF
        min_left_aabb = None
        min_right_aabb = None
        min_left_power = 0.0
        min_right_power = 0.0
        min_left_map = None
        min_right_map = None

        # 在 x、y、z 三个轴上分别尝试划分
        for axis in range(3):
            # 按该轴坐标排序光源
            sorted_map = np.argsort(centers[:, axis])
            sorted_aabbs = aabbs[sorted_map]
            sorted_powers = powers[sorted_map]

            # 从左到右扫描，累计左子树包围盒和能量
            left_aabb_low = np.minimum.accumulate(sorted_aabbs[:, 0], axis=0)[:-1]
            left_aabb_high = np.maximum.accumulate(sorted_aabbs[:, 1], axis=0)[:-1]
            left_powers = np.cumsum(sorted_powers)[:-1]

            # 从右到左扫描，累计右子树包围盒和能量
            right_aabb_low = np.minimum.accumulate(sorted_aabbs[::-1, 0], axis=0)[::-1][1:]
            right_aabb_high = np.maximum.accumulate(sorted_aabbs[::-1, 1], axis=0)[::-1][1:]
            right_powers = np.cumsum(sorted_powers[::-1])[::-1][1:]

            # 计算左右子树的面积与启发式代价 E × A
            size_left  = left_aabb_high - left_aabb_low
            size_right = right_aabb_high - right_aabb_low
            area_left  = size_left[:, 0]  * size_left[:, 1]  + size_left[:, 1]  * size_left[:, 2]  + size_left[:, 2]  * size_left[:, 0]
            area_right = size_right[:, 0] * size_right[:, 1] + size_right[:, 1] * size_right[:, 2] + size_right[:, 2] * size_right[:, 0]
            cost = (area_left * left_powers + area_right * right_powers)

            # 记录当前轴上最小代价划分
            axis_min_cost_idx = np.argmin(cost)
            if cost[axis_min_cost_idx] < min_cost:
                min_cost = cost[axis_min_cost_idx]
                min_left_aabb = np.stack([left_aabb_low[axis_min_cost_idx], left_aabb_high[axis_min_cost_idx]])
                min_right_aabb = np.stack([right_aabb_low[axis_min_cost_idx], right_aabb_high[axis_min_cost_idx]])
                min_left_power = left_powers[axis_min_cost_idx]
                min_right_power = right_powers[axis_min_cost_idx]
                min_left_map = sorted_map[:axis_min_cost_idx + 1]
                min_right_map = sorted_map[axis_min_cost_idx + 1:]

        return min_left_aabb, min_right_aabb, min_left_power, min_right_power, min_left_map, min_right_map

    # 递归构建函数：深度优先构建 BVH
    def build_dfs_recursive(self, cur_aabb, cur_power, indices, aabbs, centers, powers, depth, pbar):
        """
        参数：
            cur_aabb  : 当前节点包围盒
            cur_power : 当前节点总能量
            indices   : 当前节点包含的光源索引
            depth     : 当前节点深度
        """
        # 若只剩一个光源 → 叶子节点
        if len(indices) == 1:
            self.depth = max(self.depth, depth)
            cur_node_ptr = self.building_cache['node_ptr']
            self.nodes[cur_node_ptr] = LightBVHNode(
                left=-1, right=-1,
                aabb=AABB(cur_aabb[0], cur_aabb[1]),
                data=indices[0],
                power=cur_power
            )
            self.building_cache['node_ptr'] += 1
            self.id2node[indices[0]] = cur_node_ptr
            pbar.update(1)
            return cur_node_ptr

        # 创建当前节点（内部节点）
        cur_node_ptr = self.building_cache['node_ptr']
        self.nodes[cur_node_ptr] = LightBVHNode(
            left=-1, right=-1,
            aabb=AABB(cur_aabb[0], cur_aabb[1]),
            data=-1, power=cur_power
        )
        self.building_cache['node_ptr'] += 1

        # 使用启发式划分左右子树
        left_aabb, right_aabb, left_power, right_power, left_map, right_map = \
            LightBVH.split_node(aabbs, centers, powers)

        # 拆分左右子树数据
        left_indices, left_aabbs, left_centers, left_powers = indices[left_map], aabbs[left_map], centers[left_map], powers[left_map]
        right_indices, right_aabbs, right_centers, right_powers = indices[right_map], aabbs[right_map], centers[right_map], powers[right_map]

        # 递归构建左右子树
        left_node_ptr = self.build_dfs_recursive(left_aabb, left_power, left_indices, left_aabbs, left_centers, left_powers, depth + 1, pbar)
        self.nodes[cur_node_ptr].left = left_node_ptr
        self.nodes[left_node_ptr].parent = cur_node_ptr

        right_node_ptr = self.build_dfs_recursive(right_aabb, right_power, right_indices, right_aabbs, right_centers, right_powers, depth + 1, pbar)
        self.nodes[cur_node_ptr].right = right_node_ptr
        self.nodes[right_node_ptr].parent = cur_node_ptr

        return cur_node_ptr

    # 构建入口：从光源列表生成 LightBVH
    def build(self, lights, verbose=True):
        # 初始化缓存
        self.building_cache = {'node_ptr': 0}
        self.depth = 0

        if lights.shape[0] > 0:
            pbar = tqdm(total=lights.shape[0], desc='Building BVH', disable=not verbose)

            # 预处理光源数据
            aabbs = [lights[i].AABB() for i in range(lights.shape[0])]
            aabbs = np.array([[aabb.low, aabb.high] for aabb in aabbs], dtype=np.float32)
            centers = (aabbs[:, 0] + aabbs[:, 1]) / 2
            powers = np.array([lights[i].power() for i in range(lights.shape[0])], dtype=np.float32)
            indices = np.arange(lights.shape[0])

            # 根节点包围盒与总能量
            root_aabb = np.stack([aabbs[:, 0].min(axis=0), aabbs[:, 1].max(axis=0)])
            root_power = np.sum(powers)

            # 递归构建 BVH
            self.build_dfs_recursive(root_aabb, root_power, indices, aabbs, centers, powers, 1, pbar)
            pbar.close()

        # 设置节点总数
        self.node_cnt[None] = self.building_cache['node_ptr']
        del self.building_cache

24.3 光源采样

在构建好 LightBVH 之后，我们就可以利用它在渲染过程中高效地执行光源采样了。

采样从 BVH 的根节点开始。我们根据每个节点的能量和空间与几何关系估计贡献，自顶向下随机选择路径，直到抵达一个叶节点，即具体的光源。

其核心实现如下：

@ti.func
def sample(self, query_point, query_normal):
    prob = 1.0
    ptr = 0
    # 从根节点开始遍历 BVH
    while self.nodes[ptr].data == -1:
        cur_node = self.nodes[ptr]
        left_node = self.nodes[cur_node.left]
        right_node = self.nodes[cur_node.right]

        # 估计左右子节点的采样权重
        w_l = AABB_query_weight(left_node.aabb, query_point, query_normal) * left_node.power + 1e-8
        w_r = AABB_query_weight(right_node.aabb, query_point, query_normal) * right_node.power + 1e-8

        # 计算左右分支的采样概率
        p_l = w_l / (w_l + w_r)
        p_r = 1 - p_l

        # 根据随机数决定采样方向
        if ti.random() < p_l:
            ptr = cur_node.left
            prob *= p_l
        else:
            ptr = cur_node.right
            prob *= p_r

    return self.nodes[ptr].data, prob

整个过程与传统的 BVH 相交遍历在形式上非常相似，但目的完全不同：我们不是在寻找“哪个节点被击中”，而是在整棵树中逐层按潜在光贡献进行重要性采样。

在每一层，我们估计左右子节点相对于当前查询点的潜在贡献，这个贡献综合了节点包围盒的可见性、距离衰减与能量大小。根据两者的相对权重，我们随机选择进入哪一个子节点。

最终到达叶节点时，所选中的光源并非等概率抽样的结果，而是在每层都经过重要性采样后的联合分布。此时返回的 prob 表示该光源在整个 LightBVH 中被选中的总概率，其与该光源对查询点的贡献大致呈正比。

采样的关键在于如何为每个节点（AABB）分配合理的权重。 AABB_query_weight() 函数给出了一个简洁而高效的启发式估计：

@ti.func
def AABB_query_weight(aabb, query_point, query_normal):
    radius_v = (aabb.high - aabb.low) * 0.5
    radius2 = radius_v.dot(radius_v)
    center = (aabb.high + aabb.low) * 0.5
    is_inside = all(query_point > aabb.low) and all(query_point < aabb.high)
    cos_theta = 1.0
    if not is_inside:
        flag = query_normal > 0
        aabb_point = ti.select(flag, aabb.high, aabb.low)
        cos_theta = (aabb_point - query_point).normalized().dot(query_normal)
    dist_v = query_point - center
    dist2 = max(radius2, dist_v.dot(dist_v))
    return max(0, cos_theta) / dist2

它主要从三个方面进行加权估计：

距离衰减：距离越远，节点对该点的潜在贡献越小，因此以 $1/d^2$ 衰减。
朝向因子：通过 $\cos\theta$ 考虑表面法线方向与节点方向的一致性，仅对可见区域增加权重。
体积修正：使用 AABB 的半径平方 radius2 作为最小距离，避免采样时对非常近的节点出现极端权重。

这种启发式方法虽非严格的可见性积分，但在实践中非常有效。它在采样时优先考虑那些既靠近、又可能可见的光源包围盒，从而在大规模场景中显著提高采样的稳定性与收敛速度。

得益于 LightBVH 的层次化结构，我们能够在包含上千个光源的场景中实现 O(log N) 复杂度的光源采样。虽然不如直接按功率采样的 O(1)，但是 LightBVH 的采样考虑了光源对击中点的潜在贡献，能显著减少了直接光估计的方差，也为后续的多重重要性采样（MIS）提供了更好的基础分布。

24.4 概率查询

实际做多重重要性采样（MIS）时，除了做直接光照估计的光源采样，另一支按 BSDF 采样的光线也可能与光源相交，这时为了计算 BSDF 采样分支上光源的贡献，我们还需要知道某个光源被采样的概率。

LightBVH 可以通过反向遍历路径节点来计算该概率：

@ti.func
def query(self, id, query_point, query_normal):
    prob = 1.0
    ptr = self.id2node[id]
    # 从叶节点一路向上遍历
    while ptr != 0:
        cur_node = self.nodes[ptr]
        parent_node = self.nodes[cur_node.parent]
        # 找到兄弟节点
        if parent_node.left != ptr:
            sibling_ptr = parent_node.left
        else:
            sibling_ptr = parent_node.right
        sibling_node = self.nodes[sibling_ptr]

        # 当前节点与兄弟节点的相对权重
        w_c = AABB_query_weight(cur_node.aabb, query_point, query_normal) * cur_node.power + 1e-8
        w_s = AABB_query_weight(sibling_node.aabb, query_point, query_normal) * sibling_node.power + 1e-8

        # 在父节点层面的选择概率
        prob *= w_c / (w_c + w_s)
        ptr = cur_node.parent
    return prob

这段代码的逻辑正好与采样函数相反。采样时我们自顶向下选择节点，而这里则自底向上回溯选择路径。

在每一层，光源所在的子节点 cur_node 与其兄弟节点 sibling_node 之间的权重比值决定了它在父节点层面被选中的概率。通过将这些层级概率相乘，我们就能得到光源被整棵 LightBVH 结构采样到的最终概率。

24.5 效果对比

在我们的实现中，LightBVH 既可以与 直接光源采样（NEE） 结合，也可以进一步融入 多重重要性采样（MIS），在光源采样与 BSDF 采样之间动态平衡估计误差，从而显著提升图像收敛速度与视觉稳定性。

为了验证 LightBVH 在复杂场景下的效果，我们在一个多光源环境中进行了系统对比实验。

实验设置：

场景：Diorama of cyberpunk city （来源：Sketchfab）

每像素采样数：128 spp

路径跟踪算法：随机游走

采样策略：均匀采样

最朴素的随机游走算法，每次反射方向均匀采样球面。由于没有任何形式的重要性采样，光线极少命中发光区域，噪声极为明显，尤其是在距离光源较远的地方，例如屋顶的空调外机，亮度分布极不稳定。

路径跟踪算法：随机游走

采样策略：BSDF 重要性采样

通过根据表面材质分布（BSDF）进行采样，光线更容易集中在反射或高光方向。在低粗糙度区域（例如水坑与汽车表面）中，高光的噪声显著减少，图像收敛速度明显提升。

不过，由于仍未考虑光源分布，阴影区域与漫反射面仍存在明显噪声。

路径跟踪算法：直接光照估计

采样策略：BSDF 重要性采样 + 光源功率采样

引入 Next Event Estimation (NEE) 后，每次弹射会额外采样一个光源进行直接光照估计。此时，噪声进一步降低，特别是在高粗糙度或漫反射区域，收敛速度有明显改善。但由于光源功率采样只按能量大小分布，忽略了几何关系与可见性，对局部遮挡或小光源的采样仍不理想，例如灯牌对附近墙壁的照明噪声较大。

路径跟踪算法：直接光照估计

采样策略：BSDF 重要性采样 + LightBVH 采样

当使用 LightBVH 进行光源采样后，采样权重不仅考虑光源能量，还融合了距离、朝向与可见性启发式。这使得光线更容易命中对当前表面点贡献更大的光源区域。

在图中可以看到，灯牌对墙面的照明更加均匀稳定，小范围强光区域（如霓虹灯与广告牌边缘）的噪声显著降低。

路径跟踪算法：直接光照估计

采样策略：BSDF 重要性采样 + LightBVH 采样 + 多重重要性采样

结合本文介绍的所有技术：光源采样由 LightBVH 驱动，BSDF 采样与光源采样通过 MIS 权重平衡。

这种策略在所有材质、光照条件下都表现稳定—— 无论是反射高光、漫反射阴影还是多层遮挡，都能保持低噪声。整体收敛速度最高，图像质量最接近理想的参考结果。

在相同采样数下与 Blender Cycles 渲染器的结果比较一下：

左：Blender Cycles 渲染结果 | 右：基于 Taichi 的渲染器结果

虽然噪声控制仍有改进空间，但已经十分接近了。

总结

策略	优点	缺点
均匀采样	实现最简单	高噪声，极慢收敛
BSDF IS	对镜面高光收敛快	忽略光源分布
NEE + 功率采样	有效减少直接光噪声	忽略几何与可见性
NEE + LightBVH	采样更贴合光照贡献	仍需与 BSDF 平衡
LightBVH + MIS	最优解	实现复杂，需维护 BVH

在多光源、复杂几何的真实场景中， LightBVH + MIS 的组合能在相同采样预算下实现最低噪声水平。这也是现代路径追踪系统在处理大规模光源时的核心方法之一。

下一步

在本文中，我们系统地从物理建模与算法优化两个角度推进了渲染器的进化，使其从早期的经验性路径追踪逐步成长为一个具备物理一致性与采样效率的完整系统。

我们首先从渲染方程与蒙特卡洛方法出发，奠定了基于辐射度量学的数学基础，并引入重要性采样理论，使路径追踪具备可控的方差与物理正确性。随后，我们深入讨论了微平面材质模型（Microfacet Model），通过法线分布函数、几何遮挡项与菲涅尔效应的组合，构建了基于 GGX 的物理可解释 BRDF，并实现了 Principled BRDF 的实际版本，让金属、塑料、水面等材质表现更加真实。

接着，我们实现了直接光源采样、多重重要性采样 (MIS)，环境光重要性采样与LightBVH 光源层次结构，使渲染器能够高效地处理复杂光照，显著降低噪声。

至此，我们的渲染器已具备以下特征：

完整的基于物理的光传输框架（渲染方程 + 蒙特卡洛采样）；
可扩展的微平面 BRDF 模型，支持真实的材质表现；
高效的光源采样体系，支持多光源与环境光的分层重要性采样。

它或许还算不上完美，但已经具备了现代路径追踪器的核心功能。

接下来还可以做很多改进，比如加入 降噪（Denoising），提升低采样图像的质量；或者实现 GPU Wavefront Path Tracing，让路径调度更高效、更贴近现代 GPU 管线。

不过，写到这里，作者得去赶 CVPR 了（笑）。后续想到什么，就随缘更新吧。