序言
在最小可行的光线追踪器里,我们只实现了光线与球体的相交,用最简单的方式跑出第一张图像。这个起点足以展示光线追踪的魅力,但若要渲染更复杂、更真实的场景,还需要补上几块关键的拼图。
在《用 Taichi 学光线追踪》系列的第二篇中,延续第一篇“光线与几何体相交”的基础,我们将让渲染器真正迈向复杂场景:引入 BVH(Bounding Volume Hierarchy)加速结构,以显著减少射线与物体的相交开销;支持 三角网格,使得渲染对象不再局限于球体,而可以加载任意模型;并实现一个初步的 材质系统,赋予表面更丰富的外观表现。
这些功能在当时的学习过程中是一个重要的分水岭:有了 BVH,性能才足以支撑更大规模的场景;有了网格,才能看到熟悉的几何模型逐渐成像;有了材质,画面才第一次具备“质感”。本文会像第一篇一样,着重记录思路与方法,而不是追求功能的完备性,力求让读者能够理解核心概念并快速实践。
如果说第一篇是点亮了第一张像样的图像,那么这一篇就是为渲染器装上了扩展的骨架与外壳,让它开始具备真正成长为完整渲染器的可能。
11. 代码优化
代码:GitHub
在上一章中,我们已经完成了一个最小可行的光线追踪器:它能够生成射线、计算交点,并成功渲染出第一张像样的图像。然而,如果仔细测试,会发现运行速度并不理想。当场景复杂度提升,或者采样数增加时,性能瓶颈会迅速显现出来。
因此,本章的任务是对已有代码进行 整理与优化。优化的目标不仅是“更快”,更是让代码结构更合理,为后续扩展铺平道路。这里我们重点从两个方面入手:
- 核函数融合(kernel fusion):减少内核之间的数据交互开销,提高并行效率。
- 冗余计算消除:避免在循环中重复执行可以提前计算的逻辑,减少无谓的资源消耗。
在保持逻辑正确性的前提下,这些改动能让渲染器的性能和可维护性都更进一步。
11.1 核函数融合
在上一章的实现中,渲染流程大致分为以下几个步骤:
- 在一个 kernel 中生成相机射线,并写入全局 field
rays。 - 在另一个 kernel 中读取这些射线,执行与场景的相交计算。
- 在外层 Python 循环中,重复执行上述 kernel 若干次,以完成每个像素的多次光线追踪采样。
这种写法虽然直观,但存在两个明显问题:
- 内核调用过多:每次采样都需要在 Python 层循环中触发 kernel,造成额外的调用开销。
- 全局 field 冗余:相机射线先写入
rays,再从rays读出,实际上是多余的中间存储,增加了内存访问压力。
优化思路
通过 核函数融合(kernel fusion),我们可以把这些步骤合并到一个更紧凑的 kernel 里:
- 在 kernel 内直接完成 spp 循环。
- 每次采样时直接生成相机射线,而不是依赖全局 field。
- 在同一个 kernel 内完成射线追踪、颜色累积与结果写回。
这样,Python 层的循环被 GPU/CPU 并行化替代,减少了 kernel 启动和全局内存访问的开销。
优化后的代码
新实现将采样和追踪逻辑统一放进同一个 kernel:
@ti.kernel
def shader(world: ti.template(), camera: ti.template()):
# GPU 并行多重采样
for i, j, k in ti.ndrange(resolution[0], resolution[1], spp // batch):
c = Vec3f(0.0)
for b in range(batch):
ray = camera.get_ray(i, j) # 直接生成射线,不依赖全局 field
for _ in range(propagate_limit):
propagate_once(ray, world)
if ray.end == 1:
break
if ray.end == 1:
c += backbround_color(ray) * ray.l / spp
image[i, j] += c
def render(world: World, camera: Camera):
shader(world, camera)
post_processing()
相比旧版,主要优化点在于:
- 消除全局 field
rays:相机射线直接在 kernel 内生成,避免了显存中间存储与加载。 - 融合 spp 循环:将采样循环放入 kernel 内,用
ti.ndrange把像素和采样维度一起并行化。
这里有一个特殊的设置:batch,即每个线程内部连续处理的采样数。它的作用是减少总的线程数量。
理论上,更大的并行度通常意味着更好的性能,但在实践中需要考虑两点限制。一是Taichi 的索引范围,ti.ndrange 的索引总数不能超过 2^32,否则会溢出。这意味着当分辨率和 spp 很大时,如果每个采样都分配一个线程,就可能超过上限。二是硬件线程资源,GPU 能同时调度的线程数量有限(受 SM 数量、寄存器、显存等因素制约)。如果一次性启动的线程过多,反而会导致调度和资源竞争开销,性能下降。
因此,batch 的引入是一种折中,把采样任务适度集中到单个线程内执行,从而减少总线程数量,避免溢出或过度调度。一般来说,batch 的选择需要结合 分辨率、spp 和硬件条件进行调节。在低分辨率、低 spp 下可以设置为 1(最大化并行度);而在高分辨率或大规模采样时,适当增大 batch,能带来更稳定的性能表现。
当然,Camera 类也需要做对应的调整,以支持在 kernel 内直接生成射线。核心变化在于渲染前先准备好投影参数和坐标轴向量,然后在 get_ray 方法中根据像素坐标和随机扰动生成具体的光线:
@ti.data_oriented
class Camera:
# 提前准备好所需变量
def prepare_render(self):
trans = rotate(self.yaw, self.pitch, self.roll)
ratio = self.resolution[1] / self.resolution[0]
self.view_width = 2 * math.tan(math.radians(self.fov) / 2)
self.view_height = self.view_width * ratio
self.direction = trans @ Vec3f([0.0, 0.0, -1.0])
self.width_axis = trans @ Vec3f([1.0, 0.0, 0.0])
self.height_axis = trans @ Vec3f([0.0, 1.0, 0.0])
@ti.func
def get_ray(self, i, j):
target = self.focal_length * (
self.direction
+ ((i + ti.random(ti.f32)) / self.resolution[0] - 0.5) * self.view_width * self.width_axis
+ ((j + ti.random(ti.f32)) / self.resolution[1] - 0.5) * self.view_height * self.height_axis
)
sample = sample_in_disk()
origin = self.aperture / 2.0 * (sample[0] * self.width_axis + sample[1] * self.height_axis)
return Ray(
ro=self.position + origin,
rd=(target - origin).normalized(),
l=Vec3f([1.0, 1.0, 1.0])
)
这样一来,相机射线的生成完全内联进 kernel,不再依赖全局 field 存储。
按和函数融合优化后的代码,渲染流程更加紧凑,同时显著降低了 Python 与 Taichi kernel 之间的切换开销。实际测试时,在较大的 spp 下,性能提升会非常明显。
11.2 冗余计算消除
在上一版实现中,HitRecord 结构被设计成直接保存交点的完整信息,包括位置、法向量和材质属性:
HitRecord = ti.types.struct(point=Vec3f, normal=Vec3f, t=ti.f32, material=Material)
这种方式虽然直观,但存在一个明显的问题:在场景求交循环中,每个几何体都会生成这样一个完整的交点记录。然而,最终只有最近的交点才会被真正保留,其余几何体的计算结果都被丢弃。换句话说,大量的法线计算、材质拷贝,以及结构体的内存读写,都是白白浪费的。
随着场景中几何体数量的增加,这种冗余计算会成为性能瓶颈。因此,我们需要重新设计交点数据的表达方式,将计算过程拆解成 “轻量求交” 和 “延迟补全” 两个阶段。
轻量求交
几何体在求交时,只需要返回一个包含 t(交点距离)的最小记录。例如球体可以定义:
SphereHitRecord = ti.types.struct(t=ti.f32)
@ti.dataclass
class Sphere:
@ti.func
def hit(self, ray):
oc = ray.ro - self.center
a = 1
b = 2.0 * ti.math.dot(oc, ray.rd)
c = ti.math.dot(oc, oc) - self.radius**2
discriminant = b**2 - 4 * a * c
record = SphereHitRecord(0.0)
record.t = -1
if discriminant >= 0:
sqrt_discriminant = ti.sqrt(discriminant)
record.t = (-b - sqrt_discriminant) / (2.0 * a)
if record.t < 1e-4 and self.material.transparency:
record.t = (-b + sqrt_discriminant) / (2.0 * a)
return record
在循环中,每个几何体只需计算得到交点距离 t 并返回(过程量可按需前添加到 HitRecord 中,方便后续使用),逻辑非常简单:要么相交,记录下距离;要么不相交,t = -1。这样可以大大减少循环体内部的计算量。
延迟补全交互信息
当我们确定了最终命中的几何体及其 t 值后,再调用一个单独的函数去计算交点位置、法向量和材质等完整信息。这部分定义为 SurfaceInteraction:
SurfaceInteraction = ti.types.struct(
point=Vec3f,
normal=Vec3f,
albedo=Vec3f,
metallic=ti.i32,
roughness=ti.f32,
ior=ti.f32,
transparency=ti.i32
)
@ti.dataclass
class Sphere:
@ti.func
def get_surface_interaction(self, si: ti.template(), ray, record):
si.point = ray.ro + record.t * ray.rd
si.normal = (si.point - self.center).normalized()
si.albedo = self.material.albedo
si.metallic = self.material.metallic
si.roughness = self.material.roughness
si.ior = self.material.ior
si.transparency = self.material.transparency
return si
这样一来,只有最近的交点会触发这部分计算,避免了重复开销。
修改场景求交循环
配合上面的两个阶段,场景求交逻辑就可以写得更清晰:
@ti.data_oriented
class World:
@ti.func
def hit(self, ray):
sphere_hit_id = -1
hit_t = -1.0
sphere_hit_record = SphereHitRecord(0.0)
si = SurfaceInteraction()
for i in range(self.size):
record = self.spheres[i].hit(ray)
if record.t >= 1e-4 and (hit_t < 0 or record.t < hit_t):
sphere_hit_id = i
hit_t = record.t
sphere_hit_record = record
hit = sphere_hit_id >= 0
if hit:
self.spheres[sphere_hit_id].get_surface_interaction(si, ray, sphere_hit_record)
if ray.rd.dot(si.normal) > 0: # 背面修正
si.normal = -si.normal
si.ior = 1 / si.ior
return hit, si
在循环里,几何体只负责提供“候选交点的距离”,最后再由被命中的几何体负责生成完整的交点信息。
通过这样的改造,我们实现了以下优化:
- 避免重复计算:法线与材质的计算只会在真正命中的几何体上执行一次。
- 减少内存开销:循环中保存的数据从“完整交点结构”简化为计算出交点距离
t的最小记录。
从架构角度看,这相当于把原本混在一起的“几何求交”和“表面交互”两个概念彻底拆开,让渲染管线的每个环节都更单一、更清晰,提升可维护性。
11.3 速度测试
除了前面介绍的两项主要优化外,代码里还有一些必要的配套修改:例如 BSDF 的输入由 HitRecord 改为 SurfaceInteraction,propagate_once 的接口也随之调整;同时,World 类和相机部分的实现也做了小幅改造,以适应新的数据流。
具体实现还请读者自行参考代码。
完成这些修改后,我们可以对比优化前后的运行速度。下面展示的是在相同场景和采样配置下的渲染结果:

优化后的渲染时间为 50.58s,而优化前为 124.03s,速度提升约 2.5 倍。
这类“低层次的优化”通常不会改变算法本身,但通过减少冗余计算和内存搬运,可以显著提升性能。
12. 层次包围体(BVH)
代码:GitHub
在上一节中,我们通过核函数融合和冗余计算消除,让光线追踪器的运行效率得到了明显提升。但这些手段主要作用在实现层面,当场景复杂度增加到成百上千个几何体时,性能瓶颈依然会出现。原因很直观:每条光线仍然必须与场景中的所有几何体进行逐一求交。
举个例子,如果场景包含 10 万个三角形,而图像生成需要发射上百万条光线,那么潜在的相交测试次数将达到万亿级别。这种规模的计算量,即使在 GPU 上也难以承受。要真正解决问题,就必须减少“无意义的求交”,也就是避免让每条光线都遍历整个场景。
层次包围体(Bounding Volume Hierarchy, BVH)正是为此设计的一种经典的加速结构,它通过空间层次划分,帮助我们在复杂场景中高效定位潜在的相交区域。
12.1 加速原理
BVH 的基本思想是利用树状层次化的包围盒来组织几何体,从而在射线求交时快速排除掉大多数与光线无关的对象。
具体来说,BVH 将场景中的几何体递归划分为若干子集,每个子集都由一个紧致的轴对齐包围盒(Axis-Aligned Bounding Box, AABB)包裹。最外层的根节点覆盖整个场景,然后逐层二分,直到叶子节点仅包含少量几何体为止。这样,就得到了一棵自顶向下的二叉树结构,每一层都在空间上起到“过滤器”的作用。
当一条射线进入 BVH 时,算法首先检测它是否与根包围盒相交。如果没有交点,可以立即判定这条射线与场景完全无关;如果有交点,则递归的查询两个子树,重复上述过程。随着递归深入,射线会不断被引导到少数可能相交的叶子节点,其他庞大的子树则被整块跳过。这样,真正需要与射线逐一测试的几何体数量会急剧减少。
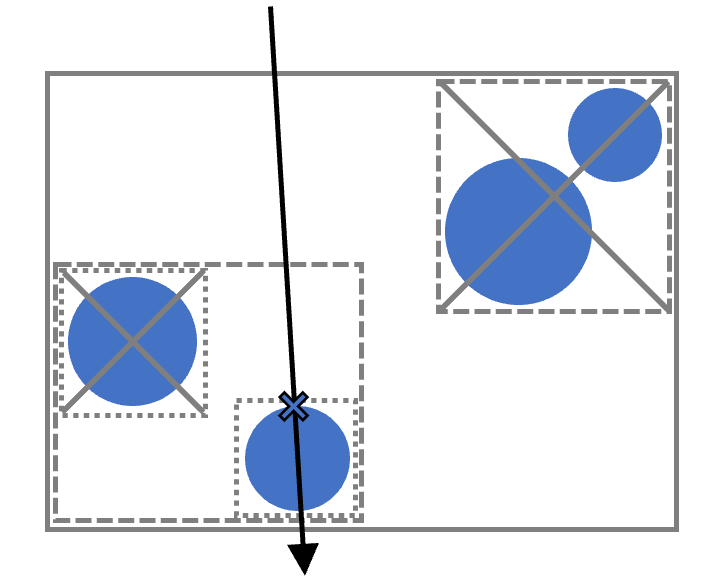
图示光线避免了与带 × 子树的几何体计算相交。
这一分层剔除机制,将原本 O(N) 的逐一相交检测,降低为接近 O(log N) 的复杂度。换句话说,即使场景中包含数十万甚至上百万个三角形,射线通常也只需访问其中极小的一部分。正因如此,BVH 已经成为光线追踪渲染器中应用最广泛的加速结构。
12.2 存储 BVH
建好的 BVH 树需要以 GPU 友好的方式存储,以便在射线遍历中高效访问节点和几何体。与 CPU 上常用的动态指针树不同,GPU 对指针跳转和动态内存分配支持有限,因此我们通常采用 扁平化数组 来存储 BVH 节点和几何体。
INF = 114514114514
BVHNode = ti.types.struct(
left=ti.i32, right=ti.i32, # 左右子节点索引,-1 表示叶子节点
aabb=AABB, # 当前节点的轴对齐包围盒
data=ti.i32, size=ti.i32, # 叶子节点的几何体起始索引和数量
next=ti.i32 # 深度优先遍历中下一个节点索引
)
@ti.data_oriented
class BVH:
def __init__(self, primitive_type, hit_record_type, size):
size = max(size, 16)
self.primitive_type = primitive_type
self.hit_record_type = hit_record_type
self.nodes = BVHNode.field(shape=(2 * size - 1,)) # 存储节点
self.primitives = primitive_type.field(shape=(size,)) # 存储几何体
self.node_cnt = ti.field(ti.i32, shape=())
self.primitive_cnt = ti.field(ti.i32, shape=())
self.depth = 0
每个 BVHNode 包含以下核心信息:
aabb:节点对应的轴对齐包围盒,用于快速判定射线是否可能相交;left、right:左右子节点索引,-1 表示叶子节点;data、size:叶子节点中几何体的起始索引和数量;next:用于 无栈深度优先遍历,指向深度优先顺序中的下一个节点。对于内部节点,表示其左右子树遍历完成后的下一个节点;对于叶子节点,表示下一个要访问的节点。
所有节点连续存储在数组 nodes 中,叶子节点通过 data 和 size 直接索引对应几何体数组 primitives。内部节点仅使用 aabb 表示空间范围,不存储几何体数据。
为什么节点预分配长度为 2 * size - 1 的数组呢?我们的 BVH 最终最多有 size 个叶子节点(每个叶子存一个几何体或一组几何体)。完整的二叉树中,内部节点的数量总是比叶子节点少 1,所以总节点数为 2 * size - 1。这保证我们为所有节点分配了足够的空间,无需动态扩容。
这种存储方式有几个优势:
- GPU 友好:节点和几何体都连续存储在数组中,访问模式连续,充分利用 GPU 内存带宽;
- 无需动态分配:所有节点和几何体在构建时就确定大小,渲染时无需动态分配或释放内存;
- 高效遍历:利用
next指针可以在无需显式栈或递归调用的情况下实现深度优先遍历,充分利用 GPU 的并行特性和数组化存储的连续内存带宽。
示意图如下:
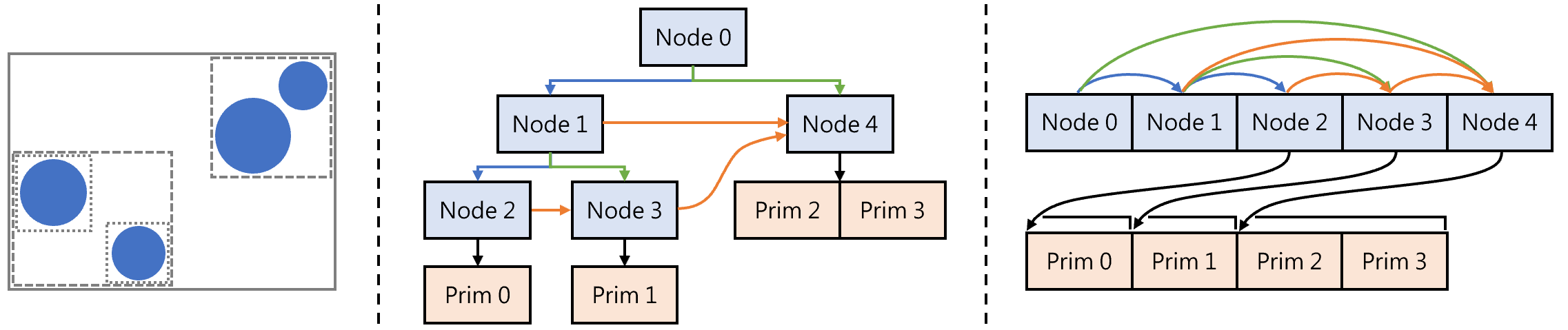
这种 扁平化存储 + 数组索引 的方式,是现代 GPU 光线追踪器中广泛使用的 BVH 内存布局方法。
12.3 构造 BVH
构造 BVH 的关键问题在于:如何将场景中的几何体划分为合理的子集。 划分得好,树的层次结构就更加平衡,射线遍历时也能高效地剔除无关对象;划分得差,则可能导致某些节点过于庞大或分布不均,从而影响性能。
这里我们先实现最简单的一种策略:沿当前包围盒的最长轴均匀划分。直观地说,最长轴方向往往代表了场景分布最“拉伸”的维度,从这个方向切分,通常能得到较为均匀的子集。
下面给出一个简单的实现示例,输入都是 numpy 数组,返回值也都是 numpy 数组:
@ti.data_oriented
class BVH:
@staticmethod
def split_node(cur_aabb, aabbs, centers):
# 1. 找到当前包围盒最长的轴
size = cur_aabb[1] - cur_aabb[0]
axis = np.argmax(size)
# 2. 按照几何体中心点在该轴上的坐标排序
sorted_map = np.argsort(centers[:, axis])
mid = len(sorted_map) // 2
# 3. 将对象划分为等大的左右两部分
left_map, right_map = sorted_map[:mid], sorted_map[mid:]
# 4. 分别计算左右子集的 AABB
left_aabbs = aabbs[left_map]
right_aabbs = aabbs[right_map]
left_low = left_aabbs[:, 0].min(axis=0)
left_high = left_aabbs[:, 1].max(axis=0)
right_low = right_aabbs[:, 0].min(axis=0)
right_high = right_aabbs[:, 1].max(axis=0)
left_aabb = np.stack([left_low, left_high])
right_aabb = np.stack([right_low, right_high])
return left_aabb, right_aabb, left_map, right_map
这段代码完成了一个典型的 BVH 节点划分过程:
- 选择轴:找到当前 AABB 的最长轴。
- 排序划分:根据几何体中心在该轴上的坐标排序,并从中点一分为二。
- 计算子包围盒:分别求出左右子集的整体包围盒。
这种方法虽然简单,但在很多情况下已经能显著提升遍历效率。
递归执行划分操作,直到所有几何体都被分配到叶子节点为止,我们就能得到一棵完整的 BVH 树。下面给出一个较为完整的实现示例。
def build_dfs_recursive(self, cur_aabb, indices, aabbs, centers, depth, pbar):
# 叶子节点:直接存储几何体
if len(indices) == 1 or depth >= self.building_cache['max_depth']:
self.depth = max(self.depth, depth)
cur_node_ptr = self.building_cache['node_ptr']
self.nodes[cur_node_ptr] = BVHNode(
left=-1, right=-1,
aabb=AABB(cur_aabb[0], cur_aabb[1]),
data=self.building_cache['primitive_ptr'],
size=len(indices)
)
self.building_cache['node_ptr'] += 1
# 更新 next 指针:叶子节点的 next 指向深度优先顺序中的下一个节点
self.nodes[cur_node_ptr].next = self.building_cache['node_ptr']
# 将几何体写入 primitives 数组
for i in indices:
self.primitives[self.building_cache['primitive_ptr']] = self.building_cache['primitives'][i]
self.building_cache['primitive_ptr'] += 1
pbar.update(1)
return cur_node_ptr
# 内部节点:递归划分
cur_node_ptr = self.building_cache['node_ptr']
self.nodes[cur_node_ptr] = BVHNode(
left=-1, right=-1,
aabb=AABB(cur_aabb[0], cur_aabb[1]),
data=-1
)
self.building_cache['node_ptr'] += 1
# 划分左右子集
left_aabb, right_aabb, left_map, right_map = BVH.split_node(cur_aabb, aabbs, centers)
left_indices, left_aabbs, left_centers = indices[left_map], aabbs[left_map], centers[left_map]
right_indices, right_aabbs, right_centers = indices[right_map], aabbs[right_map], centers[right_map]
# 递归构建左子树
left_node_ptr = self.build_dfs_recursive(left_aabb, left_indices, left_aabbs, left_centers, depth + 1, pbar)
self.nodes[cur_node_ptr].left = left_node_ptr
# 递归构建右子树
right_node_ptr = self.build_dfs_recursive(right_aabb, right_indices, right_aabbs, right_centers, depth + 1, pbar)
self.nodes[cur_node_ptr].right = right_node_ptr
# 更新 next 指针:
# 对于内部节点,next 指向其左右子树遍历完成后的下一个节点
# 此时 build_dfs_recursive 已经构建完左、右子树,所以 node_ptr 正好指向当前节点的下一个 DFS 节点
self.nodes[cur_node_ptr].next = self.building_cache['node_ptr']
return cur_node_ptr
next 指针逻辑说明
-
叶子节点: 叶子节点不再有子节点,
next指向深度优先顺序中下一个节点的位置。构建时直接用self.building_cache['node_ptr']赋值,因为下一个节点正好是数组中当前指针的位置。 -
内部节点: 对于内部节点,
next指向其左右子树遍历完成后的下一个节点。在当前节点的子树 DFS 递归构建完成后,self.building_cache['node_ptr']指向当前节点子树遍历完成后的下一个节点,所以next指针指向self.building_cache['node_ptr']。
最后是入口函数 build,负责初始化缓存、计算整体包围盒并启动递归:
def build(self, primitives, max_depth=None, verbose=True):
# 初始化构建缓存
self.building_cache = {
'primitives': primitives,
'max_depth': max_depth or INF,
'node_ptr': 0,
'primitive_ptr': 0,
}
self.depth = 0
if len(primitives) > 0:
pbar = tqdm(total=len(primitives), desc='Building BVH', disable=not verbose)
# 预处理:计算每个几何体的 AABB 和中心点
aabbs = [obj.AABB() for obj in primitives]
aabbs = np.array([[aabb.low, aabb.high] for aabb in aabbs], dtype=np.float32)
centers = (aabbs[:, 0] + aabbs[:, 1]) / 2
indices = np.arange(len(primitives))
# 计算整个场景的 AABB 作为根节点
root_aabb = np.stack([aabbs[:, 0].min(axis=0), aabbs[:, 1].max(axis=0)])
# 启动递归
self.build_dfs_recursive(root_aabb, indices, aabbs, centers, 1, pbar)
pbar.close()
# 设置节点和几何体计数
self.node_cnt[None] = self.building_cache['node_ptr']
self.primitive_cnt[None] = self.building_cache['primitive_ptr']
del self.building_cache
这个实现采用了 深度优先递归构建,并且在构建过程中就将几何体和节点数据写入 Taichi 的 field 中,便于后续 GPU 端的加速遍历。这种构造方式虽然是比较朴素的“中点划分法”,但它能够快速生成一棵较为平衡的 BVH,构建速度和遍历效率都能满足大多数应用需求。
12.4 遍历 BVH
在 CPU 上,我们通常使用递归来遍历 BVH,因为指针跳转和函数调用开销相对较小,递归自然且直观。然而在 GPU 上情况不同:GPU 线程以 SIMD(Single Instruction, Multiple Data) 模式同时执行相同的指令流,如果不同线程沿不同路径递归访问 BVH,就会产生 分支发散,导致部分线程空闲,降低并行效率。
另一种直观方法是让每个线程维护一个独立的显式栈,用来存储回溯节点。然而这种方式在 GPU 上代价很高:每个线程需要额外的寄存器存储栈,限制了可并行线程数量,同时增加了访问开销,降低整体性能。
为了解决这个问题,我们采用 无栈深度优先搜索 (stackless DFS)。在 BVH 构建阶段,就为每个节点计算出深度优先顺序下的 下一个节点索引,存储在 next 字段中。遍历时,无论节点是内部节点还是叶子节点,都可以直接通过 next 跳转到下一个待访问节点:
- 内部节点:
next指向其整个子树遍历完成后的下一个节点(即在 DFS 顺序下紧跟当前子树之后的节点); - 叶子节点:
next指向深度优先顺序下的下一个节点(可能是兄弟节点或某个祖先的右子节点)。
所有节点和几何体都连续存储在数组中,使 GPU 线程可以沿数组顺序访问,无需栈或递归。每个线程只需维护一个索引变量 ptr 就能完成整个 DFS 遍历,同时充分利用 GPU 的内存带宽和 SIMD 并行能力。这种方法既避免了分支发散和栈开销,又保证了高效的 BVH 遍历。
@ti.func
def hit(self, ray):
hit_id = -1 # 命中的几何体索引
hit_t = -1.0 # 最近交点距离
hit_record = self.hit_record_type(0.0) # 命中记录初始化
ptr = 0 # 从根节点开始遍历
vis = BVHTraverseStatistics() # 用于统计遍历效率,可视化性能
# 无栈遍历 BVH
while ptr < self.node_cnt[None]:
vis.nfe_aabb += 1
# 测试射线与当前节点包围盒是否相交
aabb_in, aabb_t = aabb_hit(self.nodes[ptr].aabb, ray)
# 如果包围盒被射线击中,并且交点距离比当前命中更近
if aabb_in and (hit_t < 0 or aabb_t < hit_t):
# 叶子节点
if self.nodes[ptr].data >= 0:
vis.nfe_primitive += self.nodes[ptr].size
for i in range(self.nodes[ptr].data, self.nodes[ptr].data + self.nodes[ptr].size):
record = self.primitives[i].hit(ray)
if record.t >= 1e-4 and (hit_t < 0 or record.t < hit_t):
hit_id = i
hit_t = record.t
hit_record = record
# 遍历完叶子节点后,直接跳到 next
ptr = self.nodes[ptr].next
# 内部节点
else:
# 优先访问 left 子节点(DFS 顺序)
ptr = self.nodes[ptr].left
# 射线未击中或当前节点交点不更近
else:
ptr = self.nodes[ptr].next
return hit_id, hit_record, vis
逻辑拆解
-
主循环:无栈遍历 BVH
循环条件
ptr < self.node_cnt[None]保证遍历在有效节点范围内。 -
AABB 相交测试
调用
aabb_hit判断射线是否穿过当前节点包围盒,返回是否相交和最近交点距离aabb_t。@ti.func def aabb_hit(aabb, ray): invdir = 1 / ray.rd i = (aabb.low - ray.ro) * invdir o = (aabb.high - ray.ro) * invdir tmax = ti.max(i, o) tmin = ti.min(i, o) t1 = ti.min(tmax[0], ti.min(tmax[1], tmax[2])) t0 = ti.max(tmin[0], ti.max(tmin[1], tmin[2])) return t1 >= t0 and t1 > 0, t0若射线与包围盒相交,并且交点距离比当前命中更近,处理当前节点;否则直接跳转到
next。 -
叶子节点处理
遍历叶子节点包含的几何体,调用各几何体的
hit方法进行精确相交测试并更新最近交点信息hit_id、hit_t、hit_record。处理完叶子节点后,直接跳转到next节点。 -
内部节点处理
优先访问
left子节点,实现深度优先遍历。
上面的函数根据光线遍历完 BVH 后,返回命中的几何体索引 hit_id、命中记录 hit_record 和统计信息 vis。
12.5 速度测试
最后,我们修改 World 类,使用 BVH 替代原来的暴力遍历进行交点测试:
@ti.data_oriented
class World:
def __init__(self, spheres=[]):
self.spheres = spheres
self.spheres_BVH = None
def add(self, sphere):
self.spheres.append(sphere)
def build_BVH(self, max_depth=None):
if self.spheres_BVH is None:
self.spheres_BVH = BVH(Sphere, SphereHitRecord, len(self.spheres))
self.spheres_BVH.build(self.spheres, max_depth)
@ti.func
def hit(self, ray):
si = SurfaceInteraction()
sphere_hit_id, sphere_hit_record, vis = self.spheres_BVH.hit(ray)
hit = sphere_hit_id >= 0
if hit:
self.spheres_BVH.primitives[sphere_hit_id].get_surface_interaction(si, ray, sphere_hit_record)
if ray.rd.dot(si.normal) > 0:
si.normal = -si.normal
si.ior = 1 / si.ior
return hit, si, vis
速度测试结果如下,使用 BVH 的渲染耗时为 10.59s,比暴力遍历的耗时 50.58s 快 5x 倍。
下图可视化了使用 BVH 加速时,射线与 AABB 和几何体的求交次数:


可以看到,使用 BVH 加速后,相比于暴力遍历的约 500 次与几何体的求交,射线与 AABB 和几何体的求交次数大大减少,总计为平均 52.8 次,达到了数量级上的减少。这一差距随着场景复杂度的增加,会更加显著。
13. 更好的 BVH 划分
代码:GitHub
在前面的章节中,我们已经实现了一个可以正常工作的 BVH,并成功利用它加速了射线与场景的求交。BVH 的核心思想是“分而治之”:通过递归地把场景几何体划分到层次化的包围盒中,从而让射线快速排除掉大部分不可能命中的物体。
然而,BVH 的效率高度依赖于 划分策略。一个好的划分能够让射线在遍历时尽量少进入无效的子节点,并且在真正进入叶子节点时,里面包含的几何体数量也足够少,从而减少求交开销。相反,如果划分不合理,射线遍历会进入很多不必要的分支,导致加速效果大打折扣。
在之前的实现里,我们采用了最简单的 中点划分(Equal Split):在最长轴上取几何体中心的中点,把物体分成数量基本相等的两半。这种方式实现容易,效果也还可以,但并没有真正考虑射线查询的代价。为了得到更高质量的 BVH,我们需要更好的划分策略。
13.1 空间均匀划分
在中点划分的基础上,一个最直接的改进是采用 空间均匀划分(Middle Split)。它的思路很简单:在当前节点的包围盒上,找到最长的轴,然后在这个轴的几何中心位置插入一个切分平面,把整个空间平分为左右两半。之后,再根据物体与切分平面的关系,将它们分配到左子节点或右子节点中。
这种方法和中点划分的差别在于切分依据的不同。中点划分是以物体数量为基准,保证每个子节点里几何体的数量大致相等;而空间均匀划分则完全基于空间范围,不考虑几何体数量,而是让空间本身对半分。
def split_node_middle(cur_aabb, aabbs, centers):
# 1. 找到最长轴
size = cur_aabb[1] - cur_aabb[0]
axis = np.argmax(size)
# 2. 找到切分平面
middle = 0.5 * (centers[:, axis].min() + centers[:, axis].max())
mask = centers[:, axis] < middle
# 3. 划分子集
left_map = np.nonzero(mask)[0]
right_map = np.nonzero(~mask)[0]
left_aabbs = aabbs[left_map]
right_aabbs = aabbs[right_map]
left_low = left_aabbs[:, 0].min(axis=0)
left_high = left_aabbs[:, 1].max(axis=0)
right_low = right_aabbs[:, 0].min(axis=0)
right_high = right_aabbs[:, 1].max(axis=0)
left_aabb = np.stack([left_low, left_high])
right_aabb = np.stack([right_low, right_high])
return left_aabb, right_aabb, left_map, right_map
这种方法的优势在于实现简单、构建速度快,并且能够生成在空间上更为规整的划分结果。它不依赖物体数量,而是直接将当前节点的空间范围沿最长轴对半切开,这使得在大规模或分布均匀的场景中,能够快速得到比较平衡的树结构,避免了中点划分中因强行均分数量而导致的子节点包围盒过度重叠。同时,由于只需要一次几何中心的比较而无需排序,它在需要频繁重建 BVH 的动态场景中也更为高效。
但是,空间均匀划分虽然比最原始的中点划分更贴近几何空间,但依旧存在局限性。由于它完全按照空间范围来切分,并不考虑物体的分布情况,当场景中的几何体分布高度不均匀时,就可能出现一边子节点几乎塞满所有物体,而另一边却几乎为空的极端情况。这些问题使得 middle split 虽然在构建速度上占优,但在高质量渲染或复杂场景中,往往还需要更智能的划分策略来进一步优化 BVH 的结构。
13.2 表面积启发式
前面我们介绍了中点划分和空间均匀划分,它们的优点在于简单高效,但共同的问题是没有真正去度量 射线遍历的代价。在实际渲染中,我们更关心的是“射线穿过这个节点时,平均要花多少成本”,而这正是 表面积启发式 (SAH, Surface Area Heuristic) 想要解决的核心问题。
SAH 的出发点非常直观:一个射线与某个包围盒相交的概率,和这个包围盒的表面积成正比。也就是说,表面积越大,被射线击中的机会越高。于是,在做 BVH 划分时,我们不仅要考虑几何体的数量,还要结合左右子节点的表面积来权衡划分的好坏。
具体来说,SAH 定义了一个代价函数:
\[C = C_{trav} + \frac{S_L}{S_P} N_L C_{isect} + \frac{S_R}{S_P} N_R C_{isect}\]这里,$C_{trav}$ 表示进入一个节点的遍历开销,$C_{isect}$ 表示一次射线–几何体求交的开销;$S_P$ 是父节点的表面积,$S_L$ 和 $S_R$ 分别是左右子节点的表面积;$N_L$ 和 $N_R$ 则是左右子节点包含的几何体数量。
直观理解是这样的:
- 遍历一个内部节点本身需要付出 $C_{trav}$ 的代价;
- 射线进入左子节点的概率大约是 $S_L / S_P$,进入右子节点的概率大约是 $S_R / S_P$;
- 一旦进入子节点,就要和其中 $N_L$ 或 $N_R$ 个几何体进行求交测试。
于是,整个划分的“期望代价”就能通过上式估计出来。构建 BVH 时,我们会在一系列候选切分中选择 代价 $C$ 最小 的那个,从而得到一个对射线遍历最优的划分;如果不切分的代价最小(因为遍历树也有代价),那么就选择不切分。
SAH 的优势显而易见:它直接面向遍历效率进行优化,得到的 BVH 通常比中点划分或空间均匀划分高效得多,也被广泛应用在现代渲染器和光线追踪引擎中。缺点同样也很明显——要评估所有可能的切分位置,就需要反复计算子节点表面积和几何体分布,带来了相当大的构建开销。因此,SAH 更适合离线渲染或静态场景,而在需要实时重建的场景中,人们往往会采用一些近似或快速版本的 SAH 来折中性能和效率。
这里,我们实现最朴素的 SAH 算法,即直接计算每个可能的切分对应的代价,然后选择代价最小的那个。
@staticmethod
def split_node_sah(cur_aabb, aabbs, centers):
# 当前节点包围盒的表面积
size_total = cur_aabb[1] - cur_aabb[0]
area_total = size_total[0] * size_total[1] + size_total[1] * size_total[2] + size_total[2] * size_total[0]
# 初始化最优结果
min_cost = len(aabbs) # 初始代价 = 几何体数量
min_axis, min_idx = -1, -1 # 最优划分的轴和位置
min_left_aabb = min_right_aabb = None
min_left_map = min_right_map = None
# 遍历 3 个坐标轴
for axis in range(3):
# 按物体中心点排序
sorted_map = np.argsort(centers[:, axis])
sorted_aabbs = aabbs[sorted_map]
# 前缀扫描:得到左子树 AABB
left_aabb_low = np.minimum.accumulate(sorted_aabbs[:, 0], axis=0)[:-1]
left_aabb_high = np.maximum.accumulate(sorted_aabbs[:, 1], axis=0)[:-1]
# 后缀扫描:得到右子树 AABB
right_aabb_low = np.minimum.accumulate(sorted_aabbs[::-1, 0], axis=0)[::-1][1:]
right_aabb_high = np.maximum.accumulate(sorted_aabbs[::-1, 1], axis=0)[::-1][1:]
# 计算左右子树的表面积与数量
size_left = left_aabb_high - left_aabb_low
size_right = right_aabb_high - right_aabb_low
area_left = size_left[:, 0] * size_left[:, 1] + size_left[:, 1] * size_left[:, 2] + size_left[:, 2] * size_left[:, 0]
area_right = size_right[:, 0] * size_right[:, 1] + size_right[:, 1] * size_right[:, 2] + size_right[:, 2] * size_right[:, 0]
cnt_left = np.arange(len(sorted_map) - 1) + 1
cnt_right = len(sorted_map) - cnt_left
# SAH 代价函数
cost = 1 + (area_left * cnt_left + area_right * cnt_right) / area_total
# 更新最优划分
axis_min_cost_idx = np.argmin(cost)
if cost[axis_min_cost_idx] < min_cost:
min_cost = cost[axis_min_cost_idx]
min_axis = axis
min_idx = axis_min_cost_idx
min_left_aabb = np.stack([left_aabb_low[axis_min_cost_idx], left_aabb_high[axis_min_cost_idx]])
min_right_aabb = np.stack([right_aabb_low[axis_min_cost_idx], right_aabb_high[axis_min_cost_idx]])
min_left_map = sorted_map[:axis_min_cost_idx + 1]
min_right_map = sorted_map[axis_min_cost_idx + 1:]
# 返回结果(是否成功划分,以及左右子树的 AABB 和索引映射)
if min_axis >= 0:
return True, min_left_aabb, min_right_aabb, min_left_map, min_right_map
else:
return False, None, None, None, None
核心逻辑拆解
-
前缀扫描和后缀扫描构造子树 AABB
left_aabb_low = np.minimum.accumulate(sorted_aabbs[:, 0], axis=0)[:-1] left_aabb_high = np.maximum.accumulate(sorted_aabbs[:, 1], axis=0)[:-1] right_aabb_low = np.minimum.accumulate(sorted_aabbs[::-1, 0], axis=0)[::-1][1:] right_aabb_high = np.maximum.accumulate(sorted_aabbs[::-1, 1], axis=0)[::-1][1:]左子树:从前往后累积最小值和最大值,得到前缀 AABB。右子树:从后往前累积,得到后缀 AABB。这样就能在
O(N)的时间里得到所有可能划分的子树包围盒。 -
计算每个候选划分的 SAH 代价
size_left = left_aabb_high - left_aabb_low size_right = right_aabb_high - right_aabb_low area_left = ... area_right = ... cnt_left = np.arange(len(sorted_map) - 1) + 1 cnt_right = len(sorted_map) - cnt_left cost = 1 + (area_left * cnt_left + area_right * cnt_right) / area_totalSAH 的核心:
- 子树越小(面积小),被射线击中的概率就越低;
- 子树内几何体越少,交点测试开销也越低。
这里的
cost恰好对应公式:
其中 $C_{trav} = C_{isect} = 1$。
相比简单的中点划分或空间均匀划分,SAH 能够更准确地估计遍历时的开销,从而得到 更高质量、更高效率的 BVH。
13.3 性能比较
通过在场景地面上随机摆放一些球体,并让相机垂直看向场景,我们可以比较不同划分策略的渲染效率并做可视化。
def random_scene(num=1000):
world = World()
for _ in range(num):
center = Vec3f([3 - 6 * random.random(), 0, 3 - 6 * random.random()])
albedo = Vec3f([random.random(), random.random(), random.random()])
sphere = Sphere(center, 0.2, material=Material(albedo=albedo, roughness=random.random(), metallic=0, ior=1.5, transparency=0))
world.add(sphere)
return world
camera = Camera(resolution)
camera.set_position(Vec3f([0, 100, 0]))
camera.set_direction(0, -90, 0)
camera.set_fov(4)
camera.set_len(100, 0.2)
camera.prepare_render()
world = random_scene()
划分可视化
为了直观地比较不同 BVH 划分策略的效果,我们在场景中放置了 16 个球体,并绘制了 BVH 遍历的开销热力图。图中的颜色深浅表示射线访问节点的数量:颜色越亮表示该射线需要更多的求交计算。
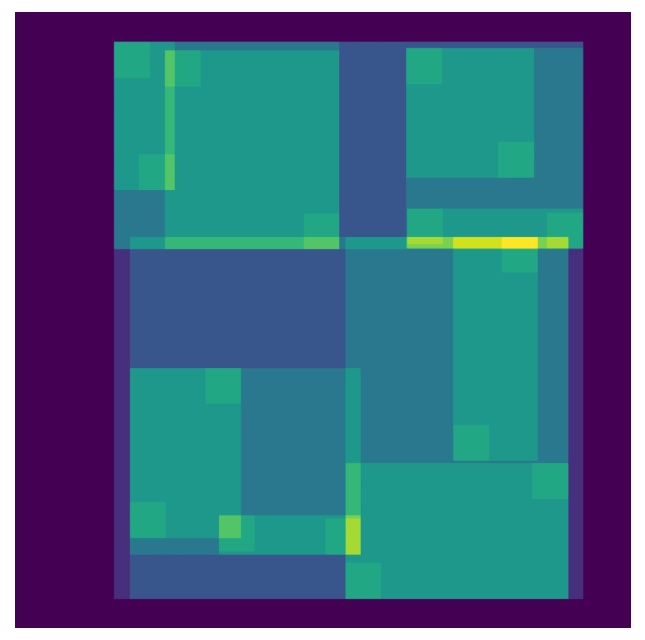


从左到右依次为三种 BVH 划分策略的对比:中点划分(Equal Split)的平均求交次数为 5.6,它只考虑几何体数量来划分节点,导致一些稀疏区域被集中到同一子树,热点区域范围较大;空间均匀划分(Middle Split)的平均求交次数为 4.9,它根据空间范围切分节点,使子树在空间上更加规整,热点区域稍微分散,相比中点划分减少了冗余求交;而SAH 划分(Surface Area Heuristic)的平均求交次数最低,为 4.6,它直接优化射线遍历代价,高热点区域被有效切分,节点利用率更高,因此在大多数场景中能够获得最佳遍历性能。
性能对比
接着,我们在场景中随机放置了 1000 个球体,进行压力测试,并记录射线遍历所需的平均求交次数和运行时间。通过比较不同策略的渲染效率,可以清晰看出划分方法对 BVH 性能的影响:
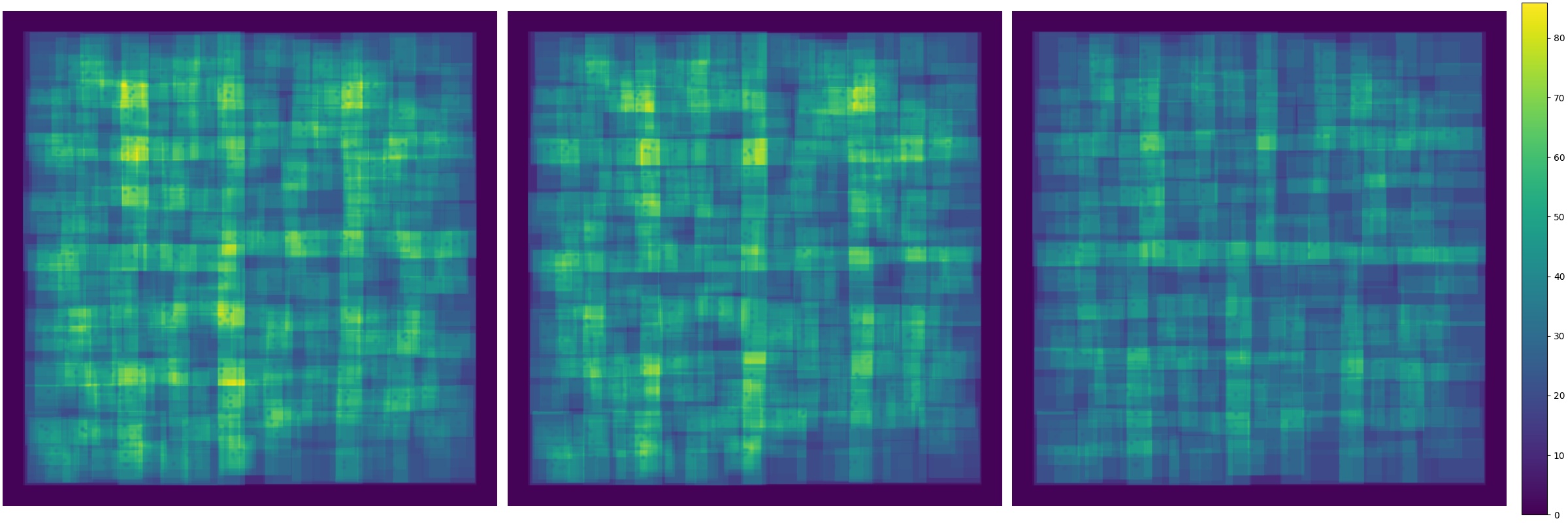
| 划分策略 | 平均求交次数 | 渲染用时 |
|---|---|---|
| 中点划分(Equal Split) | 29.5 (AABB) + 3.3 (几何体) | 6.70s |
| 空间均匀划分(Middle Split) | 28.2 (AABB) + 3.3 (几何体) | 5.89s |
| SAH 划分(Surface Area Heuristic) | 21.4 (AABB) + 5.2 (几何体) | 4.99s |
使用第 10 节中的场景测试:

| 划分策略 | 平均求交次数 | 渲染用时 |
|---|---|---|
| 中点划分(Equal Split) | 50.8 (AABB) + 2.0 (几何体) | 10.48s |
| 空间均匀划分(Middle Split) | 28.6 (AABB) + 2.0 (几何体) | 6.30s |
| SAH 划分(Surface Area Heuristic) | 23.0 (AABB) + 2.1 (几何体) | 5.75s |
可以看到,SAH 虽然在叶子节点中增加了一些几何体求交,但由于显著减少了 AABB 测试的次数,整体效率最高;相比之下,中点划分和空间均匀划分在节点层面产生了更多冗余遍历,导致运行时间更长。最终,SAH 的渲染速度提升了接近 40%,展现出更高质量 BVH 的优势。
14. 三角网格
代码:GitHub
到目前为止,我们的示例主要以球体为核心展开。球体的优势在于相交测试简单,非常适合用来初步验证光线追踪中的各种算法。然而在实际渲染中,绝大多数模型并非由球体组成,而是以 三角网格 (Triangle Mesh) 的形式存储。
三角网格是图形学中最常见的几何表示方式:无论是角色模型、建筑场景,还是通过扫描得到的重建结果,几乎都会被统一表示为由海量三角形拼接而成的网格。与球体相比,三角形的最大优势在于其通用性:任意复杂的曲面都可以通过三角形离散化近似;同时,射线与三角形之间存在高效的解析相交解。现代 GPU 渲染管线更是以三角形为核心,因此,一个光线追踪器若想处理真实场景,三角网格支持就是首要条件。换句话说,能否高效处理三角网格,直接决定了渲染器能否胜任真实应用。
基于此前实现的 BVH,我们终于可以将支持扩展到大规模三角网格。接下来,我们将按步骤推进:从单个三角形的射线求交开始,再扩展到完整的三角网格,结合 BVH 进行高效遍历。
14.1 三角形的射线求交
最简单的三角形求交算法可以分为两个步骤。
第一步:射线与平面求交
给定三角形的三个顶点 $\boldsymbol{p}_0, \boldsymbol{p}_1, \boldsymbol{p}_2$,我们先计算它的法向量:
\[\boldsymbol{N} = (\boldsymbol{p}_1 - \boldsymbol{p}_0) \times (\boldsymbol{p}_2 - \boldsymbol{p}_0).\]设射线为
\[\boldsymbol{r}(t) = \boldsymbol{r}_o + t \boldsymbol{r}_d,\]其中 $\boldsymbol{r}_o$ 是射线起点,$\boldsymbol{r}_d$ 是方向向量。 交点必须满足
\[(\boldsymbol{r}(t) - \boldsymbol{p}_0) \cdot \boldsymbol{N} = 0.\]整理可得
\[t = \frac{(\boldsymbol{p}_0 - \boldsymbol{r}_o) \cdot \boldsymbol{N}}{\boldsymbol{r}_d \cdot \boldsymbol{N}}.\]则射线与三角形的交点为
\[\boldsymbol{P} = \boldsymbol{r}(t) = \boldsymbol{r}_o + t \boldsymbol{r}_d.\]如果 $\boldsymbol{r}_d \cdot \boldsymbol{N} \approx 0$,说明射线与平面平行;如果 $t < 0$,则交点落在射线起点的反向,均视为无交。
第二步:判断交点是否在三角形内部
射线与平面相交后,还需要判断交点 $\boldsymbol{P}$ 是否落在三角形 $\triangle \boldsymbol{p}_0 \boldsymbol{p}_1 \boldsymbol{p}_2$ 内部。 这里可以使用 重心坐标 (barycentric coordinates)。
对于三角形 $\triangle \boldsymbol{p}_0 \boldsymbol{p}_1 \boldsymbol{p}_2$,其所在平面上的任意一点 $\boldsymbol{P}$ 都可以表示为三点的加权和:
\[\boldsymbol{P} = w_0 \boldsymbol{p}_0 + w_1 \boldsymbol{p}_1 + w_2 \boldsymbol{p}_2, \quad \text{其中 } w_0 + w_1 + w_2 = 1.\]这组 $(w_0, w_1, w_2)$ 就是 $\boldsymbol{P}$ 的重心坐标。
- 若 $w_0, w_1, w_2 \geq 0$,则 $\boldsymbol{P}$ 在三角形内部或边界;
- 否则,$\boldsymbol{P}$ 在外部。
重心坐标可以通过 子三角形面积比 得到:
\[w_0 = \frac{\text{Area}(\boldsymbol{P} \boldsymbol{p}_1 \boldsymbol{p}_2)}{\text{Area}(\boldsymbol{p}_0 \boldsymbol{p}_1 \boldsymbol{p}_2)}, \quad w_1 = \frac{\text{Area}(\boldsymbol{P} \boldsymbol{p}_2 \boldsymbol{p}_0)}{\text{Area}(\boldsymbol{p}_0 \boldsymbol{p}_1 \boldsymbol{p}_2)}, \quad w_2 = \frac{\text{Area}(\boldsymbol{P} \boldsymbol{p}_0 \boldsymbol{p}_1)}{\text{Area}(\boldsymbol{p}_0 \boldsymbol{p}_1 \boldsymbol{p}_2)}.\]由于三角形面积可以用向量叉积表示:
\[\text{Area}(\boldsymbol{A}\boldsymbol{B}\boldsymbol{C}) = \frac{1}{2} \| (\boldsymbol{B}-\boldsymbol{A}) \times (\boldsymbol{C}-\boldsymbol{A}) \|,\]我们可以把分子分母都写成叉积形式,相除后就得到简洁的公式。
利用向量叉积与法向量 $\boldsymbol{N}$ 的关系,得到:
\[w_0 = \frac{[(\boldsymbol{p}_2 - \boldsymbol{p}_1) \times (\boldsymbol{P} - \boldsymbol{p}_1)] \cdot \boldsymbol{N}}{\|\boldsymbol{N}\|^2},\] \[w_1 = \frac{[(\boldsymbol{p}_0 - \boldsymbol{p}_2) \times (\boldsymbol{P} - \boldsymbol{p}_2)] \cdot \boldsymbol{N}}{\|\boldsymbol{N}\|^2},\] \[w_2 = 1 - w_0 - w_1.\]这样我们就得到了交点 $\boldsymbol{P}$ 的重心坐标。只需检查 $w_0, w_1, w_2$ 是否均为非负,即可判断 $\boldsymbol{P}$ 是否在三角形内部。
这里给出 Taichi 实现:
TriangleHitRecord = ti.types.struct(t=ti.f32, point=Vec3f, normal=Vec3f)
@ti.dataclass
class Triangle:
v0: Vec3f
v1: Vec3f
v2: Vec3f
material: Material
@ti.func
def hit(self, ray):
# 初始化交点记录
record = TriangleHitRecord(0.0, 0.0, 0.0)
record.t = -1
# 三条边向量
edge0 = self.v1 - self.v0
edge1 = self.v2 - self.v1
edge2 = self.v0 - self.v2
# 法线和面积相关系数
N = edge0.cross(edge1)
inv_area2 = 1.0 / N.dot(N)
# 射线与平面的交点参数
denom = ray.rd.dot(N)
if ti.abs(denom) > 1e-12:
t = (N.dot(self.v0) - ray.ro.dot(N)) / denom
if t > 1e-4:
# 计算交点
P = ray.ro + ray.rd * t
# 重心坐标
w0 = edge1.cross(P - self.v1).dot(N) * inv_area2
w1 = edge2.cross(P - self.v2).dot(N) * inv_area2
w2 = 1 - w0 - w1
# 判断是否在三角形内部
if w0 > 0 and w1 > 0 and w2 > 0:
record.t = t
record.point = P
record.normal = N.normalized()
return record
@ti.func
def get_surface_interaction(self, si:ti.template(), ray, record):
si.point = record.point
si.normal = record.normal
si.albedo = self.material.albedo
si.metallic = self.material.metallic
si.roughness = self.material.roughness
si.ior = self.material.ior
si.transparency = self.material.transparency
return si
因为计算过程交点距离并判断是否落在三角形内的过程中已经得到交点位置 point 和法向量 normal,这里我们在 HitRecord 中直接记录这两个值,在后续 get_surface_interaction 时可以省略计算过程。
14.2 Möller–Trumbore 算法
上一节中,我们使用“平面求交 + 面积法”计算射线与三角形的交点及重心坐标 $w_0, w_1, w_2$,方法直观,但需要先求交点再求面积,计算上存在一定冗余。
Möller–Trumbore 算法由 Tomas Möller 和 Ben Trumbore 于 1997 年提出,其通过将射线与三角形的求交问题转化为三元线性方程组,直接求解重心坐标,无需显式计算交点或三角形面积,从而大幅提高了计算效率,尤其适合光线追踪中的大规模三角形场景。
建立三元线性方程组
设三角形顶点为 $\boldsymbol{p}_0, \boldsymbol{p}_1, \boldsymbol{p}_2$,射线为
\[\boldsymbol{r}(t) = \boldsymbol{r}_o + t \boldsymbol{r}_d\]交点在三角形内部时可以表示为重心坐标:
\[\boldsymbol{P} = w_0 \boldsymbol{p}_0 + w_1 \boldsymbol{p}_1 + w_2 \boldsymbol{p}_2, \quad w_0 + w_1 + w_2 = 1\]代入 $w_0 = 1 - w_1 - w_2$,得到
\[\boldsymbol{r}_o + t \boldsymbol{r}_d = \boldsymbol{p}_0 + w_1 (\boldsymbol{p}_1 - \boldsymbol{p}_0) + w_2 (\boldsymbol{p}_2 - \boldsymbol{p}_0) = \boldsymbol{p}_0 + w_1 \boldsymbol{e}_1 + w_2 \boldsymbol{e}_2\]整理得三元一次方程组:
\[w_1 \boldsymbol{e}_1 + w_2 \boldsymbol{e}_2 - t \boldsymbol{r}_d = \boldsymbol{T}, \quad \boldsymbol{T} = \boldsymbol{r}_o - \boldsymbol{p}_0\]这是一个三维线性系统,未知量是 $w_1, w_2, t$,可以写成矩阵形式:
\[\underbrace{[\boldsymbol{e}_1 \quad \boldsymbol{e}_2 \quad -\boldsymbol{r}_d]}_{3\times 3} \begin{bmatrix} w_1 \\ w_2 \\ t \end{bmatrix} = \boldsymbol{T}\]克拉默法则求解
设系数矩阵为 $A = [\boldsymbol{e}_1 \quad \boldsymbol{e}_2 \quad -\boldsymbol{r}_d]$,向量 $\boldsymbol{x} = [w_1, w_2, t]^T$,则系统为 $A \boldsymbol{x} = \boldsymbol{T}$。
根据克拉默法则,若 $\det(A) \neq 0$,则:
\[w_1 = \frac{\det(A_1)}{\det(A)}, \quad w_2 = \frac{\det(A_2)}{\det(A)}, \quad t = \frac{\det(A_3)}{\det(A)}\]其中 $A_i$ 是将矩阵 $A$ 的第 $i$ 列替换为 $\boldsymbol{T}$ 后的矩阵。
三维方阵行列式与混合积
三维向量组成的行列式可以用混合积公式计算:
\[\det([\boldsymbol{a} \quad \boldsymbol{b} \quad \boldsymbol{c}]) = \boldsymbol{a} \cdot (\boldsymbol{b} \times \boldsymbol{c}) = \boldsymbol{b} \cdot (\boldsymbol{c} \times \boldsymbol{a}) = \boldsymbol{c} \cdot (\boldsymbol{a} \times \boldsymbol{b})\]将其应用到系数矩阵:
\[\det(A) = \boldsymbol{e}_1 \cdot (\boldsymbol{e}_2 \times (-\boldsymbol{r}_d)) = - \boldsymbol{e}_1 \cdot (\boldsymbol{e}_2 \times \boldsymbol{r}_d)\]定义 $\boldsymbol{p} = \boldsymbol{r}_d \times \boldsymbol{e}_2$,则 $\det(A) = \boldsymbol{e}_1 \cdot \boldsymbol{p}$。
类似地,定义 $\boldsymbol{q} = \boldsymbol{T} \times \boldsymbol{e}_1$,可以用混合积快速计算分子:
\[w_1 = \frac{\det([\boldsymbol{T} \quad \boldsymbol{e}_2 \quad -\boldsymbol{r}_d])}{\det(A)} = \frac{\boldsymbol{T} \cdot \boldsymbol{p}}{\det(A)}\] \[w_2 = \frac{\det([\boldsymbol{e}_1 \quad \boldsymbol{T} \quad -\boldsymbol{r}_d])}{\det(A)} = \frac{\boldsymbol{r}_d \cdot \boldsymbol{q}}{\det(A)}\] \[t = \frac{\det([\boldsymbol{e}_1 \quad \boldsymbol{e}_2 \quad \boldsymbol{T}])}{\det(A)} = \frac{\boldsymbol{e}_2 \cdot \boldsymbol{q}}{\det(A)}\]最终得到交点重心坐标:
\[w_0 = 1 - w_1 - w_2\]通过这种方式,我们把射线–三角形求交转化为求解三元线性方程,根据解出的重心坐标,我们得以判断交点是否在三角形内部。相比“平面求交 + 面积法”,运算量更小,更紧凑。
Taichi 实现
TriangleHitRecord = ti.types.struct(t=ti.f32)
@ti.dataclass
class Triangle:
v0: Vec3f
v1: Vec3f
v2: Vec3f
material: Material
@ti.func
def hit(self, ray):
# 初始化交点记录
record = TriangleHitRecord(-1.0)
e1 = self.v1 - self.v0
e2 = self.v2 - self.v0
T = ray.ro - self.v0
p = ray.rd.cross(e2)
det = e1.dot(p)
# 如果行列式太小,认为射线与三角形平行
if abs(det) > 1e-12:
inv_det = 1.0 / det
q = T.cross(e1)
t = e2.dot(q) * inv_det
# 如果交点在射线起点之后,则无交点
if t > 1e-4:
# 解三元一次方程组
w1 = T.dot(p) * inv_det
w2 = ray.rd.dot(q) * inv_det
w0 = 1.0 - w1 - w2
# 判断是否在三角形内部
if w0 >= 0.0 and w1 >= 0.0 and w2 >= 0.0 and t > 0.0:
record.t = t
return record
@ti.func
def get_surface_interaction(self, si:ti.template(), ray, record):
si.point = ray.ro + ray.rd * record.t
si.normal = (self.v1 - self.v0).cross(self.v2 - self.v0).normalized()
si.albedo = self.material.albedo
si.metallic = self.material.metallic
si.roughness = self.material.roughness
si.ior = self.material.ior
si.transparency = self.material.transparency
return si
14.3 使用 BVH 管理
使用上一节中实现的 BVH 管理三角形和球体,我们能够实现更高效的光线追踪:
@ti.data_oriented
class World:
def __init__(self, spheres=[], triangles=[]):
self.spheres = spheres
self.spheres_BVH = None
self.triangles = triangles
self.triangles_BVH = None
def add_sphere(self, sphere):
self.spheres.append(sphere)
def add_triangle(self, triangle):
self.triangles.append(triangle)
def build_BVH(self, max_depth=None, split_mode=BVHSplitMode.SAH):
if self.spheres_BVH is None:
self.spheres_BVH = BVH(Sphere, SphereHitRecord, len(self.spheres))
self.spheres_BVH.build(self.spheres, max_depth, split_mode)
if self.triangles_BVH is None:
self.triangles_BVH = BVH(Triangle, TriangleHitRecord, len(self.triangles))
self.triangles_BVH.build(self.triangles, max_depth, split_mode)
@ti.func
def hit(self, ray):
sphere_hit_id, sphere_hit_record, sphere_vis = self.spheres_BVH.hit(ray)
triangle_hit_id, triangle_hit_record, triangle_vis = self.triangles_BVH.hit(ray)
hit_primitive_type = -1
hit_t = 1e10
si = SurfaceInteraction()
vis = BVHTraverseStatistics()
if sphere_hit_id >= 0 and sphere_hit_record.t < hit_t:
hit_primitive_type = 0
hit_t = sphere_hit_record.t
vis.nfe_aabb += sphere_vis.nfe_aabb
vis.nfe_primitive += sphere_vis.nfe_primitive
if triangle_hit_id >= 0 and triangle_hit_record.t < hit_t:
hit_primitive_type = 1
hit_t = triangle_hit_record.t
vis.nfe_aabb += triangle_vis.nfe_aabb
vis.nfe_primitive += triangle_vis.nfe_primitive
if hit_primitive_type == 0:
self.spheres_BVH.primitives[sphere_hit_id].get_surface_interaction(si, ray, sphere_hit_record)
elif hit_primitive_type == 1:
self.triangles_BVH.primitives[triangle_hit_id].get_surface_interaction(si, ray, triangle_hit_record)
if ray.rd.dot(si.normal) > 0:
si.normal = -si.normal
si.ior = 1 / si.ior
return sphere_hit_id >= 0 or triangle_hit_id >= 0, si, vis
在 hit 函数中,我们首先调用 hit 函数计算球体和三角形的交点,并记录下距离最近的交点及其类型(球体或三角形)。然后,我们根据距离最近的交点类型,调用相应的 get_surface_interaction 函数计算交点处的表面信息,并根据入射方向调整法向量。
14.4 性能测试
我们使用经典的 Stanford Bunny 模型,配合随机球体和代表地面的两个大三角形,搭建出测试场景:
ground0 = Triangle(
Vec3f([-50,0,50]), Vec3f([50,0,50]), Vec3f([50,0,-50]),
material=Material(albedo=Vec3f([0.25, 0.25, 0.25]), roughness=0.5, metallic=0, ior=1.5, transparency=0)
)
ground1 = Triangle(
Vec3f([-50,0,50]), Vec3f([50,0,-50]), Vec3f([-50,0,-50]),
material=Material(albedo=Vec3f([0.25, 0.25, 0.25]), roughness=0.5, metallic=0, ior=1.5, transparency=0)
)
# Read mesh
mesh = trimesh.load_mesh('assets/models/bunny_3k.ply')
bounds = mesh.bounds
mesh.vertices -= bounds.mean(axis=0)
mesh.vertices /= (bounds[1] - bounds[0]).max()
mesh.vertices *= 2
mesh.vertices[:, 1] -= mesh.vertices[:, 1].min()
triangles = [
# center, plastic
Triangle(
mesh.vertices[mesh.faces[i][0]], mesh.vertices[mesh.faces[i][1]], mesh.vertices[mesh.faces[i][2]],
material=Material(albedo=Vec3f([0.8, 0.8, 0.8]), roughness=0.5, metallic=0, ior=1.5, transparency=0)
)
for i in range(len(mesh.faces))
]
mesh.vertices[:, 0] -= 2
triangles += [
# left, glass
Triangle(
mesh.vertices[mesh.faces[i][0]], mesh.vertices[mesh.faces[i][1]], mesh.vertices[mesh.faces[i][2]],
material=Material(albedo=Vec3f([0.8, 0.8, 0.8]), roughness=0, metallic=0, ior=1.5, transparency=1)
)
for i in range(len(mesh.faces))
]
mesh.vertices[:, 0] += 4
triangles += [
# right, copper
Triangle(
mesh.vertices[mesh.faces[i][0]], mesh.vertices[mesh.faces[i][1]], mesh.vertices[mesh.faces[i][2]],
material=Material(albedo=Vec3f([0.955, 0.638, 0.538]), roughness=0.2, metallic=1, ior=1.5, transparency=0)
)
for i in range(len(mesh.faces))
]
world = World(spheres=[], triangles=[ground0, ground1] + triangles)
random_spheres(world)
world.build_BVH(split_mode=BVHSplitMode.SAH)
运行示例代码,我们可以得到如下渲染效果:

为了比较三角形射线求交算法的性能,我们对同一场景进行了测试:
- 平面求交 + 面积法:22.55s
- Möller–Trumbore 算法:18.22s
可以看到,Möller–Trumbore 算法相比传统方法提高了约 20% 的计算效率。这主要得益于它直接解重心坐标,无需显式计算交点或三角形面积,减少了冗余计算。
结合 BVH 加速和Möller–Trumbore 算法,我们的 Taichi 光线追踪渲染器现在得以支持三角网格模型。
15. 着色法线
代码:GitHub
在光线追踪渲染中,法线(normal) 是决定光照效果的核心因素之一,它决定了光线与表面交互后的反弹方向。到目前为止,我们在渲染时一直使用的是三角形的几何法线(geometric normal)。几何法线由三角形的顶点位置直接计算而来,能够精确反映表面的几何形状。但仅依赖几何法线,往往会让物体表面呈现生硬的棱角,缺少真实世界中那种平滑、连续的光照效果。
这时就需要引入 着色法线(shading normal) 的概念。所谓着色法线,并不一定与物体的几何表面严格一致,而是为了获得更理想的光照表现而“人为构造”的法线方向。它可以通过多种方式生成,例如:
- 插值顶点法线:在三角形内部对顶点法线进行插值,使表面看起来更光滑;
- 法线贴图(normal mapping):通过纹理扰动着色法线,赋予平坦表面丰富的细节;
- 程序化法线:利用噪声或解析函数生成法线,进一步丰富材质表现。
不过,着色法线的引入也带来一个经典问题:着色法线与几何法线并不总是一致。这种差异可能导致背面法线、能量守恒错误等渲染问题。因此,如何正确地在渲染管线中处理二者的关系,是理解和实现真实光照效果的关键一步。
在本章节中,我们将以 插值顶点法线 为例,展示如何通过最简单的方式生成着色法线,从而让物体表面在光照下显得更加平滑自然。
15.1 插值顶点法线
顶点法线通常通过将与该顶点相邻的所有三角形法线求平均并归一化得到,它能够在一定程度上反映局部表面的整体方向。当我们在交点处对这些顶点法线进行插值时,就能得到随位置连续变化的法线方向,从而使表面在光照下显得平滑。
顶点法线本身我们不需要手动实现,可以直接使用几何库(例如 trimesh)计算得到。问题的核心在于:如何在三角形内部插值这些顶点法线。
在第 14 章中,我们已经引入了重心坐标的概念。利用它,我们可以很自然地把交点位置的权重应用到顶点法线上。设三角形三个顶点的法线为 $\boldsymbol{n}_0, \boldsymbol{n}_1, \boldsymbol{n}_2$,点 $\boldsymbol{P}$ 的重心坐标为 $(w_0, w_1, w_2)$,则交点处的着色法线为:
\[\boldsymbol{n}(\boldsymbol{P}) = \frac{w_0 \boldsymbol{n}_0 + w_1 \boldsymbol{n}_1 + w_2 \boldsymbol{n}_2}{\left\|w_0 \boldsymbol{n}_0 + w_1 \boldsymbol{n}_1 + w_2 \boldsymbol{n}_2\right\|}\]分子部分是对顶点法线的加权插值,分母部分则保证结果重新归一化为单位向量。
对于代码实现,我们修改 Triangle 类,在 hit 函数中存储计算得出的重心坐标,并在 get_surface_interaction 函数中计算插值法线:
TriangleHitRecord = ti.types.struct(t=ti.f32, w0=ti.f32, w1=ti.f32)
@ti.dataclass
class Triangle:
@ti.func
def hit(self, ray):
...
# 额外存储重心坐标
if w0 >= 0.0 and w1 >= 0.0 and w2 >= 0.0 and t > 0.0:
record.t = t
record.w0 = w0
record.w1 = w1
...
@ti.func
def get_surface_interaction(self, si:ti.template(), ray, record):
...
# 计算并存储几何法线与插值法线
si.geo_normal = (self.v1 - self.v0).cross(self.v2 - self.v0).normalized()
si.normal = (record.w0 * self.n0 + record.w1 * self.n1 + (1 - record.w0 - record.w1) * self.n2).normalized()
...
可视化结果如下:


15.2 法线一致性
在引入着色法线之后,一个需要特别注意的问题是:着色法线和几何法线可能并不一致。几何法线严格由三角形的面决定,而着色法线则可能因为插值或扰动而偏离,甚至朝向与几何法线相反。
这种不一致会带来渲染上的问题。例如,着色法线如果背向入射光线,本应被照亮的区域可能会被错误地视为背面,从而导致能量丢失或阴影异常。
因此,渲染器需要在使用着色法线时进行一定的修正,以确保画面在保持平滑效果的同时,不会出现违反物理直觉的错误结果。
1. 保证与相机的关系一致
当光线与表面相交时,几何法线与着色法线的朝向必须在相机看来保持一致。换句话说,如果几何法线指向相机,则着色法线也必须指向相机;反之亦然。
如果二者方向相反,渲染器会错误地把一个实际可见的表面判定为背面,结果就是光照能量被不恰当地丢弃,甚至出现阴影异常。
为了解决这个问题,我们需要在交点信息 si 中进行修正:当检测到几何法线和着色法线方向不一致时,就对着色法线做一次裁剪(clipping),把它强制调整到正确的半球内。
在 get_surface_interaction 函数中加入以下判断:
# 如果着色法线和几何法线的方向不一致,则修正
if si.normal.dot(ray.rd) * si.geo_normal.dot(ray.rd) < 0:
si.normal = (si.normal - 1.001 * ray.rd.dot(si.normal) * ray.rd).normalized()
推导验证如下:设光线方向为 $\boldsymbol{d}$,着色法线为 $\boldsymbol{n}_s$,几何法线为 $\boldsymbol{n}_g$。修正公式为:
\[\boldsymbol{n}_s' = \boldsymbol{n}_s - c (\boldsymbol{d}\cdot \boldsymbol{n}_s)\boldsymbol{d}, \quad c=1.001\]则修正后的投影为:
\[\boldsymbol{n}_s'\cdot \boldsymbol{d} = \boldsymbol{n}_s\cdot \boldsymbol{d} - c (\boldsymbol{n}_s\cdot \boldsymbol{d}) = (1-c)(\boldsymbol{n}_s\cdot \boldsymbol{d})\]由于 $c>1$,投影符号会翻转,即 $\boldsymbol{n}_s’\cdot \boldsymbol{d}$ 与 $\boldsymbol{n}_s\cdot \boldsymbol{d}$ 相反。结合我们只在原始着色法线与几何法线方向不一致时才应用修正,修正后 $\boldsymbol{n}_s’\cdot\boldsymbol{d}$ 会与 $\boldsymbol{n}_g\cdot\boldsymbol{d}$ 同号,从而保证了可见性判定一致。
2. 保证 BSDF 采样的半球一致性
在进行 BSDF 采样时,生成的反射方向必须保证位于几何法线的正半球,否则光线可能穿透几何表面造成不正确的光照结果。
以 Lambertian 漫反射为例,我们从单位球上采样方向 $\boldsymbol{s}$,叠加着色法线 $\boldsymbol{n}$ 得到反射方向 $\boldsymbol{r}$,并进行半球修正:
@ti.func
def _sample_lambertian(normal, geo_normal):
s = _sample_at_sphere()
r = normal + s
# 修正反射方向 r,使其位于几何法线正半球
if r.dot(geo_normal) < 0:
r = r - 2 * r.dot(geo_normal) * geo_normal
return r.normalized()
其中关键步骤是半球修正:若反射方向 $\boldsymbol{r}$ 与几何法线 $\boldsymbol{n}_g$ 夹角大于 90°(点积为负),则沿几何法线做一次反射,将其翻转到正半球。最后归一化,确保方向长度为 1。
在更复杂的微表面采样(带粗糙度的镜面反射)中,也需要类似的半球修正:
@ti.func
def _sample_normal(dir, normal, geo_normal, roughness):
s = _sample_lambertian(normal, geo_normal)
k = -dir.dot(normal)
r = dir + 2 * k * normal # 镜面反射方向
# 修正反射方向,使其位于几何法线正半球
if r.dot(geo_normal) < 0:
r = r - 2 * r.dot(geo_normal) * geo_normal
# 粗糙度插值
r = _slerp(r, s, roughness*roughness)
n = (r - dir).normalized()
return n
这样一来确保漫反射方向和镜面反射方向位于几何法线的正半球,保证了微平面法线的物理正确性。
15.3 渲染结果
在完成着色法线的插值与一致性修正后,我们可以观察渲染效果的变化。

与上一章直接使用几何法线相比,插值后的着色法线能显著平滑表面光照,使曲面过渡更加自然。
16. 环境贴图
代码:GitHub
在之前的实现中,我们为了简化背景,采用了一个从天到地的渐变色来模拟环境:天空部分是浅蓝色,地面部分是接近白色的暖色调。这种方式实现简单,能直观地填充背景。但渐变背景毕竟过于简单,缺乏真实世界中环境光的复杂细节。
在现实世界中,物体表面的光照主要来自四面八方的环境辐射,例如天空、地面和周围的建筑物反射。为了模拟这种全局环境光照,我们需要引入 环境贴图(Environment Map)。
环境贴图的基本思想是:用一张全景图像来表示来自各个方向的光照。当射线没有与场景中的几何体相交时,我们就使用它的方向在环境贴图中查询对应的颜色,并作为背景光照。这样,物体就会在真实的环境中被照亮。
16.1 HDRI
最常见的环境贴图形式是 HDRI (High Dynamic Range Image)。与普通的 LDR 图片不同,HDRI 保存了更宽的亮度范围,既能表现天空和阴影下的微弱亮度,也能表现太阳直射的强光。
在渲染中,HDRI 通常以 经纬度展开(Latitude-Longitude, LatLong) 的形式存储。例如一张 $(w, h)$ 的 HDRI 图像,可以被看作一个球体的展开:
- 水平方向对应经度($\phi$),范围 $[0, 2\pi)$;
- 垂直方向对应纬度($\theta$),范围 $[0, \pi]$。
因此,射线方向 $\boldsymbol{d} = (d_x, d_y, d_z)$ 可以转换为图像坐标 $(u, v)$:
\[u = \frac{1}{2\pi}\,\text{atan2}(d_z, d_x) + 0.5, \quad v = \frac{1}{\pi}\,\arcsin(d_y) + 0.5\]然后从图像中查询颜色。
16.2 渲染管线集成
在渲染管线中,我们希望用一张全景图来替代渐变背景。这样,射线若未击中场景物体时,就会根据方向从环境贴图中采样颜色。
下面给出一个 ImageEnvironment 类的实现。它负责:
- 贴图加载与存储:将输入图像转换为 Taichi 的 field,并且翻转/转置以对齐坐标系。
- 球面映射:将射线方向 $(d_x, d_y, d_z)$ 转换为纹理坐标 $(u, v)$。
- 双线性插值:通过四个相邻像素加权求和,获得平滑的采样结果。
@ti.data_oriented
class ImageEnvironment:
def __init__(self, img):
# 记录环境贴图的尺寸
self.width = img.shape[1]
self.height = img.shape[0]
# 存储到 Taichi field
self.map = Vec3f.field(shape=(self.width, self.height))
# 翻转 & 转置,使坐标系与渲染器方向一致
self.map.from_numpy(np.flip(img.transpose(1, 0, 2), 1))
@ti.func
def sample(self, ray):
# 将射线方向转换为球面坐标
u = (ti.math.atan2(ray.rd[2], ray.rd[0]) / (2.0 * ti.math.pi) + 0.5) * self.width
v = (ti.math.asin(ti.math.clamp(ray.rd[1], -1, 1)) / ti.math.pi + 0.5) * self.height
# 获取周围四个采样点
l = ti.math.floor(u - 0.5) + 0.5
r = l + 1.0
b = ti.math.floor(v - 0.5) + 0.5
t = b + 1.0
# 双线性插值权重
w1 = (r - u) * (t - v)
w2 = (u - l) * (t - v)
w3 = (r - u) * (v - b)
w4 = (u - l) * (v - b)
# 边界处理:水平循环,垂直 clamp
l = (l + self.width) % self.width
r = (r + self.width) % self.width
b = ti.math.clamp(b, 0, self.height - 1)
t = ti.math.clamp(t, 0, self.height - 1)
# 获取四个邻近像素
c1 = self.map[int(l), int(b)]
c2 = self.map[int(r), int(b)]
c3 = self.map[int(l), int(t)]
c4 = self.map[int(r), int(t)]
# 插值结果
color = ti.math.max(0.0, w1 * c1 + w2 * c2 + w3 * c3 + w4 * c4)
return color
在初始化时,我们需要将输入的图像写入 Taichi 的 Field。值得注意的是,Taichi 的 Field 采用列主序存储(column-major order),而常见的 NumPy 图像是行主序(row-major)。这意味着,如果我们直接写入,图像会出现坐标轴错乱的问题。
因此,加载时我们必须做两步处理:
- 转置:将图像的
(H, W, C)转换为(W, H, C),以对齐 Taichi 的存储方式; - 竖直反转:因为图像的
(i, j)像素坐标与纹理的(u, v)方向相反,需要进行上下翻转来匹配渲染器的坐标系。
这样,当射线没有交点时,我们就可以直接调用:
@ti.kernel
def shader(world: ti.template(), camera: ti.template()):
for i, j, k in ti.ndrange(resolution[0], resolution[1], spp//batch):
c = Vec3f(0.0)
for b in range(batch):
ray = camera.get_ray(i, j)
for _ in range(propagate_limit):
propagate_once(ray, world)
if ray.end == 1:
break
# 环境光照
if ray.end == 1:
c += world.env.sample(ray) * ray.l / spp
image[i, j] += c
来获得环境光照。
16.3 渲染结果
在世界的初始化中添加环境贴图:
env_map = imageio.imread('assets/textures/cayley_interior_2k.exr') / 50.0
env = ImageEnvironment(env_map)
world = World(spheres=[], triangles=[ground0, ground1] + triangles, env=env)
下面展示了环境贴图对渲染结果的影响:
环境贴图不仅决定了背景颜色,也影响了物体表面的反射和折射效果,从而显著提升了真实感。
17. 纹理和材质
代码:GitHub
在前面的实现中,我们的材质仍然是均一的:一个物体整个表面共享相同的颜色、粗糙度和金属度参数。这样的材质虽然便于验证渲染管线,但缺乏真实感——现实世界中的表面几乎总是随空间位置变化的。木材有纹理走向,大理石有花纹,金属表面可能一部分被氧化,玻璃也可能同时包含透明与磨砂区域。
为了描述这种复杂的空间变化,我们需要引入 纹理(Texture)。纹理是一张(或多张)图像,用来存储材质参数随表面坐标的分布。在现代渲染标准中,尤其是 glTF 2.0 的 PBR(Physically Based Rendering)材质模型,几乎所有表面属性都通过纹理来驱动:基础颜色(baseColor)、金属度(metallic)、粗糙度(roughness)、法线扰动(normal map)等。
同时,随着模型规模的增加,纹理管理也成为渲染系统的重要组成部分。比如多个纹理打包到一个 纹理图集(Texture Atlas) 中,就能减少渲染时的切换开销,也便于使用 Taichi 实现;在 BSDF 采样上,我们还需要考虑反射与透射的概率分配(重要性采样),以更高效地利用这些材质参数。
在本章中,我们将逐步把这些功能引入到渲染器中,让材质表现迈向真实。
17.1 glTF PBR 材质格式
在本章中,我们选用 glTF 2.0 标准,它原生支持 基于物理的渲染(Physically Based Rendering, PBR) 材质模型,并在材质格式中定义了多种参数和贴图。这些参数可以既是常量,也可以通过纹理贴图实现逐像素变化,从而准确地控制物体表面在不同位置的外观。
glTF 2.0 的材质格式基于 metallic-roughness 流程,其核心组成包括:
- 基色(Base Color):由常量颜色 baseColorFactor 和纹理 baseColorTexture 定义,决定物体的整体颜色。等同于之前的均一材质中的反照率 albedo。
- 金属性(Metallic)与粗糙度(Roughness):分别控制材质的金属特性和反射模糊程度,通常打包在同一张 metallicRoughnessTexture 中,同时受 metallicFactor 和 roughnessFactor 调节。
- 法线贴图(Normal Map):存储为 normalTexture,用于扰动几何法线,增加表面细节。
- 遮蔽(Occlusion)与自发光(Emissive):分别表现环境光遮蔽和物体自身的发光属性。在物理正确的光线追踪算法中,环境光遮蔽效应会自然出现,因此 AO 贴图通常可以忽略。自发光贴图则定义了表面的发光区域,我们将在研究光照进阶和光源建模时再引入。
相比之前的均一材质表示方式,glTF 2.0 的材质模型更符合工业标准,同时能够兼顾真实感与可移植性,是现代实时渲染和离线渲染中广泛使用的格式。
代码中,我们修改 Material 结构体,使其符合 glTF 2.0 PBR 标准:
Material = ti.types.struct(
baseColorFactor=Vec3f, # 基础颜色因子
baseColorTexture=ti.i32, # 基础颜色贴图
metallicFactor=ti.f32, # 金属度因子
roughnessFactor=ti.f32, # 粗糙度因子
metallicRoughnessTexture=ti.i32, # 金属度-粗糙度贴图
normalTexture=ti.i32, # 法线贴图
transmissionFactor=ti.f32, # 透射率
ior=ti.f32, # 折射率
)
这里的纹理贴图字段使用 ti.i32 存储索引,表示其在纹理图集中的唯一 ID。
17.2 纹理图集
在上一节中,我们为材质结构体引入了多个纹理字段。最直接的实现方式是每张纹理单独存储,但在 Taichi 中,如果每个材质的纹理数量不同,直接为每张纹理创建独立 Field 会让代码难以复用,也不方便管理。
为了解决这个问题,我们可以使用纹理图集(Texture Atlas)。纹理图集将多张纹理拼接到一张大图里,每张纹理对应图集中的一个矩形区域。在渲染时,只需通过索引和坐标换算就能访问不同的子纹理。
在 Taichi 中实现纹理图集非常自然:只需要一个 Field 存储整个图集,再用索引映射到对应子区域,就能完成采样,无需为每张纹理维护单独 Field。这种方式让材质系统更加灵活,也便于复用相同的采样逻辑,避免了针对不同数量纹理写不同代码的麻烦。
为了高效管理不同大小的纹理,我们将采用一种常用的矩形打包方法——Guillotine 算法。该算法通过递归切割,把不同尺寸的矩形依次放入图集中,简单易实现,同时空间利用率也相对较高。
Taichi 实现
Taichi 纹理图集实现的核心是将所有子纹理存储到一个 Vec3u8 Field 中,同时记录每个纹理的元信息,方便在渲染管线中查找和映射。
我们首先定义了 TextureInfo 数据结构,用于存储单张纹理的尺寸、在图集中的坐标、采样方式和环绕模式。通过 TextureFilterMode 和 TextureWrapMode,可以灵活指定纹理的插值方式和 UV 环绕策略。
TextureInfo = ti.types.struct(
filter=ti.u8,
wrap=ti.u8,
x=ti.i32,
y=ti.i32,
w=ti.i32,
h=ti.i32,
class TextureFilterMode:
NEAREST = 0
LINEAR = 1
class TextureWrapMode:
CLAMP_TO_EDGE = 0
REPEAT = 1
MIRRORED_REPEAT = 2
)
接着是核心的 TextureAtlas 类。构造函数中,我们创建了存储整张图集的 Field self.atlas,以及存储纹理信息的 Field self.info。同时维护了一个 free_rects 列表,用于实现矩形打包算法。
@ti.data_oriented
class TextureAtlas:
def __init__(self, size, max_tex_num=128):
self.size = size # 图集尺寸
self.atlas = Vec3u8.field(shape=size) # 用于存储图集的 Field
self.info = TextureInfo.field(shape=(max_tex_num,)) # 用于存储纹理信息的 Field
self.textures = [] # build 之前的缓存
self.free_rects = [] # 空闲矩形列表
添加与打包纹理
add() 函数用于将单张纹理加入到待打包列表,并分配唯一 ID。
def add(self, tex_array, tex_id=None, filter=TextureFilterMode.LINEAR, wrap=TextureWrapMode.REPEAT):
tex_size = (tex_array.shape[1], tex_array.shape[0]) # (w, h)
# 分配唯一 ID 为最小未使用的 ID
if tex_id is None:
existing_ids = [t['id'] for t in self.textures]
tex_id = 0
while tex_id in existing_ids:
tex_id += 1
self.textures.append({
'array': tex_array,
'size': tex_size,
'id': tex_id,
'filter': filter,
'wrap': wrap,
})
return tex_id
在 build() 中,我们用 Guillotine 算法将纹理打包到图集中。算法通过递归切割剩余空闲矩形,高效分配空间,同时填充 self.info 以记录纹理在图集中的位置和尺寸。注意,为了与 Taichi Field 的列主序存储对齐,我们需要对纹理数组进行转置并竖直翻转。
def _allocate_rect(self, tex_size):
"""在空闲矩形列表中寻找合适的区域并分配空间给纹理。"""
w, h = tex_size
for i, (l, b, r, t) in enumerate(self.free_rects):
# 检查当前空闲矩形是否足够放下纹理
if (r - l) >= w and (t - b) >= h:
# 占用左上角区域
# 剩余的空闲矩形分成上下和左右两部分
self.free_rects[i] = [l, b + h, r, t] # 上方剩余部分保留
self.free_rects.insert(i, [l + w, b, r, b + h]) # 右方剩余部分保留
return (l, b, l + w, b + h)
return None
def build(self):
"""将所有纹理打包进纹理图集,使用简单的 Guillotine 算法"""
# 初始化空闲矩形列表,整个图集为空闲
self.free_rects = [[0, 0, self.size[0], self.size[1]]]
# 按纹理高度、宽度降序排序(先放大的纹理,减少碎片)
self.textures.sort(key=lambda x: x['size'][0], reverse=True)
self.textures.sort(key=lambda x: x['size'][1], reverse=True)
for tex in self.textures:
# 分配矩形
rect = self._allocate_rect(tex['size'])
if rect is None:
raise MemoryError('Texture atlas overflow.')
# 保存分配信息
tex['rect'] = rect
self.info[tex['id']].x = rect[0]
self.info[tex['id']].y = rect[1]
self.info[tex['id']].w = rect[2] - rect[0]
self.info[tex['id']].h = rect[3] - rect[1]
self.info[tex['id']].filter = tex['filter']
self.info[tex['id']].wrap = tex['wrap']
# 将纹理数据拷贝到图集 Field
atlas_array = self.atlas.to_numpy()
for tex in self.textures:
l, b, r, t = tex['rect']
# 由于 Taichi Field 是列主序存储,需要转置并竖直翻转
atlas_array[l:r, b:t] = np.flip(tex['array'].transpose(1, 0, 2), axis=1)
self.atlas.from_numpy(atlas_array)
纹理采样
打包完成后,渲染时需要将纹理坐标映射到图集区域。wrap_texcoord() 函数处理 UV 环绕模式,支持 CLAMP_TO_EDGE、REPEAT 和 MIRRORED_REPEAT。
@ti.func
def wrap_texcoord(self, w, u, wrap):
o = 0
if wrap == TextureWrapMode.CLAMP_TO_EDGE:
o = ti.math.clamp(u, 0, w - 1)
elif wrap == TextureWrapMode.REPEAT:
o = (u % w + w) % w
elif wrap == TextureWrapMode.MIRRORED_REPEAT:
period = (u % (2 * w) + 2 * w) % (2 * w)
if period < w:
o = period
else:
o = (2 * w - 1) - period
return o
最终的 sample() 函数根据采样方式选择最近邻或双线性插值,并返回纹理颜色。
@ti.func
def sample(self, tex_id, uv):
info = self.info[tex_id]
u, v = uv[0] * info.w, uv[1] * info.h
color = Vec3f(0, 0, 0)
if info.filter == TextureFilterMode.NEAREST:
s, t = int(ti.math.floor(u)), int(ti.math.floor(v))
s = self.wrap_texcoord(info.w, s, info.wrap) + info.x
t = self.wrap_texcoord(info.h, t, info.wrap) + info.y
color = self.atlas[s, t] / 255.0
else:
l = ti.math.floor(u - 0.5) + 0.5
r = l + 1.0
b = ti.math.floor(v - 0.5) + 0.5
t = b + 1.0
w1 = (r - u) * (t - v)
w2 = (u - l) * (t - v)
w3 = (r - u) * (v - b)
w4 = (u - l) * (v - b)
sl = self.wrap_texcoord(info.w, int(ti.math.floor(l)), info.wrap) + info.x
sr = self.wrap_texcoord(info.w, int(ti.math.floor(r)), info.wrap) + info.x
tb = self.wrap_texcoord(info.h, int(ti.math.floor(b)), info.wrap) + info.y
tt = self.wrap_texcoord(info.h, int(ti.math.floor(t)), info.wrap) + info.y
c1 = self.atlas[sl, tb]
c2 = self.atlas[sr, tb]
c3 = self.atlas[sl, tt]
c4 = self.atlas[sr, tt]
color = ti.math.clamp((w1 * c1 + w2 * c2 + w3 * c3 + w4 * c4) / 255.0, 0, 1)
return color
这样,我们就完成了一个完整的 Taichi 纹理图集实现,支持多张纹理统一存储、灵活采样,并且便于在 PBR 渲染管线中使用。
17.3 纹理坐标插值
在支持纹理采样的渲染中,每个顶点都有对应的纹理坐标(UV 坐标),通常记为
\[\boldsymbol{t}_0=(u_0, v_0), \quad \boldsymbol{t}_1=(u_1, v_1), \quad \boldsymbol{t}_2=(u_2, v_2)\]当光线与三角形表面相交时,我们需要使用重心坐标插值(Barycentric Interpolation)计算交点对应的纹理坐标:
\[(u, v) = w_0 (u_0, v_0) + w_1 (u_1, v_1) + w_2 (u_2, v_2)\]其中 $w_0, w_1, w_2$ 为交点相对于三角形三个顶点的重心坐标。通过这种方式,可以平滑地从三角形顶点纹理坐标过渡到交点纹理坐标,从而保证纹理采样连续、自然。
在代码实现中非常简洁:
uv = record.w0 * self.t0 + record.w1 * self.t1 + (1 - record.w0 - record.w1) * self.t2
计算得到的 uv 可以直接用于纹理图集采样,为后续材质采样和法线贴图提供基础数据。
17.4 法线贴图与切线空间
在 15 章 中,我们引入了着色法线(Shading Normal)的概念,它允许用于光照计算的法线与几何法线不一致,从而实现平滑光照效果。在此基础上,我们可以进一步使用法线贴图(Normal Map)来模拟表面微观凹凸,使渲染结果呈现更多细节。法线贴图在纹理级别存储了局部法线的偏移信息,这些偏移通常定义在切线空间(Tangent Space)中,需要将其转换到世界空间进行光照计算。
切线空间空间由三条向量组成:
- T(Tangent,切线):沿纹理坐标 $u$ 方向
- B(Bitangent,副切线):沿纹理坐标 $v$ 方向
- N(Normal,法线):几何法线或插值顶点法线
在交点处,切线空间法线 $n_\text{tangent} = (n_x, n_y, n_z)$ 可以通过 TBN 基向量转换为世界空间:
\[n_\text{world} = n_x \boldsymbol{T} + n_y \boldsymbol{B} + n_z \boldsymbol{N}\]这一机制允许法线贴图精确控制光照方向,实现微小凹凸和表面细节的表现,使渲染更加真实丰富。
切线空间的构建依赖顶点位置和纹理坐标的微分关系,推导过程如下。
切线 $\boldsymbol{T}$ 和副切线 $\boldsymbol{B}$ 定义为沿纹理坐标变化的方向在世界空间的对应向量:
\[\boldsymbol{T} = \frac{\partial \boldsymbol{p}}{\partial u}, \quad \boldsymbol{B} = \frac{\partial \boldsymbol{p}}{\partial v}.\]而三角形内部一点的世界坐标和纹理坐标可以用重心坐标插值表示为
\[\boldsymbol{p} = w_0 \boldsymbol{p}_0 + w_1 \boldsymbol{p}_1 + w_2 \boldsymbol{p}_2 = \boldsymbol{p}_0 + w_1 \Delta \boldsymbol{p}_1 + w_2 \Delta \boldsymbol{p}_2,\] \[u = u_0 + w_1 \Delta u_1 + w_2 \Delta u_2, \quad v = v_0 + w_1 \Delta v_1 + w_2 \Delta v_2,\]其中
\[\Delta \boldsymbol{p}_1 = \boldsymbol{p}_1 - \boldsymbol{p}_0, \quad \Delta \boldsymbol{p}_2 = \boldsymbol{p}_2 - \boldsymbol{p}_0,\] \[\Delta u_1 = u_1 - u_0, \quad \Delta u_2 = u_2 - u_0, \quad \Delta v_1 = v_1 - v_0, \quad \Delta v_2 = v_2 - v_0.\]联立上述方程,我们希望求出切线 $\boldsymbol{T} = \frac{\partial \boldsymbol{p}}{\partial u}$ 和副切线 $\boldsymbol{B} = \frac{\partial \boldsymbol{p}}{\partial v}$。链式法则直接求偏导:
\[\boldsymbol{T} = \frac{\partial \boldsymbol{p}}{\partial u} = \frac{\partial \boldsymbol{p}}{\partial w_1} \frac{\partial w_1}{\partial u} + \frac{\partial \boldsymbol{p}}{\partial w_2} \frac{\partial w_2}{\partial u} = \Delta \boldsymbol{p}_1 \frac{\partial w_1}{\partial u} + \Delta \boldsymbol{p}_2 \frac{\partial w_2}{\partial u},\] \[\boldsymbol{B} = \frac{\partial \boldsymbol{p}}{\partial v} = \frac{\partial \boldsymbol{p}}{\partial w_1} \frac{\partial w_1}{\partial v} + \frac{\partial \boldsymbol{p}}{\partial w_2} \frac{\partial w_2}{\partial v} = \Delta \boldsymbol{p}_1 \frac{\partial w_1}{\partial v} + \Delta \boldsymbol{p}_2 \frac{\partial w_2}{\partial v}.\]方程中剩下重心坐标对 $u$ 和 $v$ 的偏导,利用纹理坐标的插值公式,可以整理出微分方程
\[\begin{bmatrix} \Delta u_1 & \Delta u_2 \\ \Delta v_1 & \Delta v_2 \end{bmatrix} \begin{bmatrix} \frac{\partial w_1}{\partial u} & \frac{\partial w_1}{\partial v} \\ \frac{\partial w_2}{\partial u} & \frac{\partial w_2}{\partial v} \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}.\]取逆矩阵,解得
\[\mathrm{det} = \Delta u_1 \Delta v_2 - \Delta u_2 \Delta v_1,\] \[\begin{bmatrix} \frac{\partial w_1}{\partial u} & \frac{\partial w_1}{\partial v} \\ \frac{\partial w_2}{\partial u} & \frac{\partial w_2}{\partial v} \end{bmatrix} = \frac{1}{\mathrm{det}} \begin{bmatrix} \Delta v_2 & -\Delta u_2 \\ -\Delta v_1 & \Delta u_1 \end{bmatrix}.\]把它代回 $\boldsymbol{T}$ 和 $\boldsymbol{B}$ 的表达式,得到
\[\boldsymbol{T} = \Delta \boldsymbol{p}_1 \frac{\partial w_1}{\partial u} + \Delta \boldsymbol{p}_2 \frac{\partial w_2}{\partial u} = \frac{\Delta v_2 \Delta \boldsymbol{p}_1 - \Delta v_1 \Delta \boldsymbol{p}_2}{\mathrm{det}},\] \[\boldsymbol{B} = \Delta \boldsymbol{p}_1 \frac{\partial w_1}{\partial v} + \Delta \boldsymbol{p}_2 \frac{\partial w_2}{\partial v} = \frac{-\Delta u_2 \Delta \boldsymbol{p}_1 + \Delta u_1 \Delta \boldsymbol{p}_2}{\mathrm{det}}.\]按照上面推导得到的公式,我们在代码中做如下实现:
# calculate TBN
dp1 = self.v1 - self.v0
dp2 = self.v2 - self.v0
duv1 = self.t1 - self.t0
duv2 = self.t2 - self.t0
f = 1.0 / (duv1[0] * duv2[1] - duv2[0] * duv1[1] + 1e-8)
N = (record.w0 * self.n0 + record.w1 * self.n1 + (1 - record.w0 - record.w1) * self.n2).normalized()
T = (f * (duv2[1] * dp1 - duv1[1] * dp2)).normalized()
B = (f * (-duv2[0] * dp1 + duv1[0] * dp2)).normalized()
17.5 材质管理与采样
在引入了纹理和法线贴图之后,我们需要对场景中的材质进行统一管理,并在光线交点处高效获取材质信息。这部分主要解决两个问题:材质存储和BSDF参数采样。
首先,我们为材质设计了一个管理类 MaterialSlots,用于存储最多 max_mat_num 个材质,每个材质包含 PBR 所需的参数以及纹理索引。材质的添加和清理都由类方法统一管理:
@ti.data_oriented
class MaterialSlots:
def __init__(self, max_mat_num=128):
self.slots = Material.field(shape=(max_mat_num,))
self.existing_ids = []
def add(self, material, mat_id=None):
# 分配最小的空闲槽位
if mat_id is None:
mat_id = 0
while mat_id in self.existing_ids:
mat_id += 1
self.slots[mat_id] = material
self.existing_ids.append(mat_id)
return mat_id
def clear(self):
self.existing_ids = []
在光线与表面交点处,我们通过 sample 函数从材质和纹理图集中获取 最终可用的 BSDF 参数:
- Base Color:先使用
baseColorFactor,再根据纹理图集中的颜色(sRGB 转线性空间)进行调制。 - Metallic 和 Roughness:先使用材质自带因子,再从
metallicRoughnessTexture采样 B/G 通道叠加调制。 - 法线贴图:从切线空间采样法线,并转换到世界空间。
- 透明度与折射率:直接读取材质属性。
@ti.func
def sample(self, texture_atlas, mat_id, uv, T, B, N):
material = self.slots[mat_id]
baseColor = material.baseColorFactor
if material.baseColorTexture != -1:
# 基色贴图采样,sRGB空间转线性空间
baseColor *= texture_atlas.sample(material.baseColorTexture, uv) ** 2.2
metallic = material.metallicFactor
roughness = material.roughnessFactor
if material.metallicRoughnessTexture != -1:
# 金属度/粗糙度贴图采样
metallicRoughness = texture_atlas.sample(material.metallicRoughnessTexture, uv)
metallic *= metallicRoughness[2] # B通道
roughness *= metallicRoughness[1] # G通道
normal = Vec3f(0, 0, 1)
if material.normalTexture != -1:
# 法线贴图采样
normal = texture_atlas.sample(material.normalTexture, uv)
normal = normal * 2.0 - 1.0
# 切线空间转世界空间
normal = (normal[0] * T + normal[1] * B + normal[2] * N).normalized()
return baseColor, metallic, roughness, normal, material.ior, material.transmissionFactor
通过这个接口,我们在光线求交阶段即可快速获得与交点关联的所有材质信息,便于后续 BSDF 采样和光照计算。
结合 17.3、17.4、17.5,我们可以实现一个完整的 get_surface_interaction 函数,在最终交点处通过采样材质和纹理图集,计算出交点处的 BSDF 参数,并填入 SurfaceInteraction 对象中:
@ti.func
def get_surface_interaction(self, si:ti.template(), ray, record, material_slots, texture_atlas):
# calculate TBN
dp1 = self.v1 - self.v0
dp2 = self.v2 - self.v0
duv1 = self.t1 - self.t0
duv2 = self.t2 - self.t0
f = 1.0 / (duv1[0] * duv2[1] - duv2[0] * duv1[1] + 1e-8)
N = (record.w0 * self.n0 + record.w1 * self.n1 + (1 - record.w0 - record.w1) * self.n2).normalized()
T = (f * (duv2[1] * dp1 - duv1[1] * dp2)).normalized()
B = (f * (-duv2[0] * dp1 + duv1[0] * dp2)).normalized()
uv = record.w0 * self.t0 + record.w1 * self.t1 + (1 - record.w0 - record.w1) * self.t2
# fill in the surface interaction
si.point = ray.ro + ray.rd * record.t
si.geo_normal = (self.v1 - self.v0).cross(self.v2 - self.v0).normalized()
si.albedo, si.metallic, si.roughness, si.normal, si.ior, si.transparency = \
material_slots.sample(texture_atlas, self.material_id, uv, T, B, N)
# if shading normal and geometric normal are not in the same direction, clip shading normal
if si.normal.dot(ray.rd) * si.geo_normal.dot(ray.rd) < 0:
si.normal = (si.normal - 1.001 * ray.rd.dot(si.normal) * ray.rd).normalized()
return si
上述关于纹理坐标插值和切线空间的推导与实现主要针对三角网格。对于球体,计算会更加直接,读者可以参考源码自行实现。
17.6 BSDF 扩展
在之前的章节中,我们的 BSDF 仅区分了金属和电介质两类简单材质。为了实现更精细的材质表现,本节将 BSDF 拓展为浮点金属度(metallic)与浮点透明度(transparency),并结合亮度重要性采样来同时处理反射与透射光线。
金属与电介质的反射与透射特性
首先回顾一下第 7 章中介绍的金属与电介质的物理特性:
-
金属(Metal): 金属表面反射光线的强度 $F^\text{m}_0=\text{albedo}$,呈现色彩偏向。金属不透光,吸收所有透射光,因此 $T^\text{m} = 0$,光线只可能被反射。白光照射下,金属表面显示出其固有颜色的反射光。
-
电介质(Dielectric): 电介质的反射率由折射率(IOR)决定,$F^\text{d}_0=\left(\frac{\text{ior}-1}{\text{ior}+1}\right)^2$,且反射是白光(无色)。透射光会被部分吸收或散射,其颜色由 albedo 调节,$T^\text{d} = (1-F^\text{d})\cdot\text{albedo}$,用于表示漫反射或折射的衰减。这种情况下,BSDF 允许同时采样反射和折射方向。
Fresnel 计算与反射/透射率
通过在上面列出的金属和电介质的反射和透射率之间进行线性插值,我们可以得到 Fresnel 反射率 $F$:
\[F_0 = \text{metallic} \cdot \text{albedo} + (1 - \text{metallic}) \cdot \left(\frac{\text{ior}-1}{\text{ior}+1}\right)^2\] \[F = F_0 + (1 - F_0) (1 - \cos\theta)^5\]和透射率 $T$:
\[F^\text{d} = F^\text{d}_0 + (1 - F^\text{d}_0) (1 - \cos\theta)^5\] \[T = (1 - \text{metallic}) \cdot (1 - F^\text{d}) \cdot \text{albedo}\]亮度重要性采样
在之前对电介质 BSDF 的处理中,因为反射率是标量,我们可以之间按这个概率采样反射/透射方向。但现在反射率和透射率均为矢量,我们需要对每条路径的亮度贡献进行权衡。
如果我们随机均匀选择反射或透射方向,很容易出现方差大、噪点多的情况——尤其当反射光和透射光亮度差异很大时。为了解决这个问题,我们可以使用亮度重要性采样(luminance-based importance sampling),按照每条路径对最终图像的亮度贡献来选择采样方向。
具体做法是,先计算反射和透射光的亮度:
\[\text{lum}(F) = 0.2126\,F_r + 0.7152\,F_g + 0.0722\,F_b,\] \[\text{lum}(T) = 0.2126\,T_r + 0.7152\,T_g + 0.0722\,T_b\]然后将它们归一化得到采样概率:
\[P_F = \frac{\text{lum}(F)}{\text{lum}(F) + \text{lum}(T)}, \quad P_T = 1 - P_F\]也就是说,亮度越高的方向被采样的概率越大,从而更有效地捕捉主要光能量。采样之后,为了保证无偏估计,我们还需要用采样概率对路径贡献进行权重修正:
\[L_\text{out}^{(F)} = \frac{F \cdot L_\text{in}}{P_F}, \quad L_\text{out}^{(T)} = \frac{T \cdot L_\text{in}}{P_T}\]这种方法遵循重要性采样原则,能显著降低反射/透射混合材质的渲染噪声,让图像更加平滑自然。
Taichi 实现
@ti.func
def _lum(c):
return 0.2126 * c.x + 0.7152 * c.y + 0.0722 * c.z
class PrincipledBSDF:
@staticmethod
@ti.func
def sample(ray: ti.template(), si: ti.template()):
# 采样微平面法线
n = _sample_normal(ray.rd, si.normal, si.geo_normal, si.roughness)
cos_theta = max(0.0, n.dot(-ray.rd))
ray.ro = si.point
# 插值 Fresnel 反射率与透射率
Fd0 = ((si.ior - 1) / (si.ior + 1))**2
F0 = si.metallic * si.albedo + \
(1.0 - si.metallic) * Fd0
F = F0 + (1.0 - F0) * (1.0 - cos_theta) ** 5
Fd = Fd0 + (1.0 - Fd0) * (1.0 - cos_theta) ** 5
T = (1 - si.metallic) * (1 - Fd) * si.albedo
# 亮度重要性采样
F_lum = _lum(F)
T_lum = _lum(T)
p_F = F_lum / (F_lum + T_lum)
p_T = 1.0 - p_F
# 采样出射方向
if ti.random() < p_F:
ray.l *= F / p_F
ray.rd = _reflect(ray.rd, n)
else:
ray.l *= T / p_T
# 透明度混合
if ti.random() < si.transparency:
ray.rd = _refract(ray.rd, n, si.ior)
else:
ray.rd = _sample_lambertian(si.normal, si.geo_normal)
17.7 渲染结果
我们为斯坦福兔子与小球的场景中的每个物体添加了材质。渲染结果如下:

18. glTF 加载
代码:GitHub
前文中,我们逐步实现了一个从光线求交、BVH 加速结构,到材质、环境贴图、PBR 渲染的完整渲染管线。
作为本文的结尾,我们结合前面实现的所有核心技术,统一应用在真实的 glTF 模型加载与渲染上。
这一步的意义在于:它不仅是对前文所有模块的全面检验,更标志着我们完成了第一个真正意义上的工业级渲染案例。 glTF 作为当今业界最流行的 3D 模型格式,内置对PBR 材质、纹理贴图、法线数据的标准化支持,几乎成为现代渲染管线的事实标准。 因此,通过导入 glTF 模型并在我们的管线中进行渲染,就能证明:我们的渲染器已经初步具备处理工业级资产的能力。
18.1 glTF 简介
glTF(GL Transmission Format) 是由 Khronos Group 制定的开放 3D 资产交换格式,被称为 “3D 界的 JPEG”。 它的出现正是为了解决 3D 模型在 游戏、影视、Web、AR/VR 等工业场景中的高效传输与渲染问题。
相比我们在前文中手工构造的测试几何,glTF 拥有以下优势:
- 工业标准:几乎所有现代引擎(Unity、Unreal、three.js、Babylon.js)都支持 glTF,使其成为 3D 模型交换的事实标准。
- 轻量高效:通过 JSON(.gltf)与二进制(.bin)或单文件(.glb)格式组织数据,既易于解析又便于 GPU 上传。
- 原生 PBR 支持:内置金属-粗糙度(Metallic-Roughness)材质模型,与我们在前文实现的 BSDF 框架高度契合。
- 完善的资源体系:包括几何顶点、索引、法线、切线、UV 坐标、贴图(颜色、法线、金属度、粗糙度、AO、发光)等,能够全面验证渲染管线的各个模块。
- 可扩展性:支持动画、蒙皮、实例化等高级特性,为未来拓展打下基础。
正因为 glTF 的这些特性,它是将本文渲染器从“教学案例”提升到工业场景可用的关键一步。
18.2 与渲染管线集成
结合前文的实现,glTF 的数据可以自然映射到我们的渲染体系中:
-
几何数据 → BVH
从 glTF 中读取 顶点坐标、法线、纹理坐标,配合三角形索引数据生成三角网格。随后将三角网格批量构造成 BVH,以加速射线求交。
-
纹理资源 → 纹理图集
glTF 提供的 BaseColor、MetallicRoughness、Normal 等贴图,可以直接对接我们前文的 纹理图集,实现多张纹理的统一管理与采样。
-
材质数据 → BSDF/Material
glTF 的
pbrMetallicRoughness定义与我们实现的 金属-粗糙度 BSDF 一一对应,参数直接映射:baseColorFactor→ 基础颜色因子metallicFactor→ 金属度roughnessFactor→ 粗糙度baseColorTexture、metallicRoughnessTexture、normalTexture→ 对应纹理图集中的索引 ID
下面的示例展示了如何使用 trimesh 解析 glTF 文件,并将其中的几何与材质信息加载到我们的渲染管线中:
@ti.data_oriented
class World:
def load_gltf(self, gltf_path):
scene = trimesh.load(gltf_path)
assert isinstance(scene, trimesh.Scene), "Only trimesh.Scene is supported"
for mesh in scene.dump():
if isinstance(mesh, trimesh.Trimesh):
# 提取材质信息
visual = mesh.visual
assert isinstance(visual, trimesh.visual.TextureVisuals)
assert isinstance(visual.material, trimesh.visual.material.PBRMaterial)
# base color
bc_factor = visual.material.baseColorFactor[:3] if visual.material.baseColorFactor else (1.0, 1.0, 1.0)
bc_tex_id = self.add_texture(np.array(visual.material.baseColorTexture)[..., :3]) \
if visual.material.baseColorTexture else -1
# metallic-roughness
m_factor = visual.material.metallicFactor or 1.0
r_factor = visual.material.roughnessFactor or 1.0
mr_tex_id = self.add_texture(np.array(visual.material.metallicRoughnessTexture)[..., :3]) \
if visual.material.metallicRoughnessTexture else -1
# normal map
normal_tex_id = self.add_texture(np.array(visual.material.normalTexture)[..., :3]) \
if visual.material.normalTexture else -1
# 注册材质
mat_id = self.add_material(Material(
baseColorFactor=bc_factor,
baseColorTexture=bc_tex_id,
metallicFactor=m_factor,
roughnessFactor=r_factor,
metallicRoughnessTexture=mr_tex_id,
normalTexture=normal_tex_id,
transmissionFactor=0.0,
ior=1.5
))
# 提取三角形
triangles = [
Triangle(
v0=mesh.vertices[mesh.faces[i][0]],
v1=mesh.vertices[mesh.faces[i][1]],
v2=mesh.vertices[mesh.faces[i][2]],
n0=mesh.vertex_normals[mesh.faces[i][0]],
n1=mesh.vertex_normals[mesh.faces[i][1]],
n2=mesh.vertex_normals[mesh.faces[i][2]],
t0=visual.uv[mesh.faces[i][0]],
t1=visual.uv[mesh.faces[i][1]],
t2=visual.uv[mesh.faces[i][2]],
mat_id=mat_id
) for i in range(len(mesh.faces))
]
self.triangles.extend(triangles)
18.3 渲染结果
在整合 glTF 支持之后,我们可以方便地导入任意开源的 glTF 模型(如 glTF-Sample-Models)来测试渲染器的表现。
效果如下图所示(示例:DamagedHelmet.glb):

可以看到,渲染出的结果已经相当不错。为了更直观地对比,我们将同一模型分别使用 Blender 的 Cycles 渲染器和我们基于 Taichi 的实现进行渲染,并将结果并列展示:


整体观感上,两者已经相当接近,但依然可以察觉到一些差异,主要集中在材质细节与光传输效果上。Blender 的 Cycles 在微表面反射、能量守恒以及全局光照的处理上更为成熟,因此材质表现更加细腻,光照也更自然。而我们的实现虽然仍然简化,但已经完整支持了 glTF 2.0 的金属度/粗糙度参数等,并能够正确反映模型的主要外观特征。
这说明我们基于 Taichi 构建的光线追踪框架在保持实现简洁的同时,已经能够达到与专业渲染器较为接近的效果。未来随着在 BSDF 建模、全局光照与重要性采样方面的进一步改进,我们有望继续缩小与工业级渲染器的差距。
为自己鼓鼓掌吧!
下一步
在本文中,我们为渲染器引入了空间加速结构(BVH),并扩展了对三角形网格与材质贴图的支持。现在我们已经能够处理复杂的几何场景,并高效加载标准 glTF 模型,初步具备了通用渲染器的雏形。
然而,与成熟渲染器相比,我们的实现仍存在明显差距,主要集中在两个方面:
- 材质建模:目前对反射的处理仍然比较粗糙,还没有引入基于物理的微表面分布的模型(例如 GGX)。这让金属和高光材质的表现力受限,看起来缺乏真实感。
- 光传输模拟:当前实现基本依赖最基础的路径追踪思路,但尚未用蒙特卡洛积分的数学原理系统指导采样与光能计算(例如重要性采样),物理正确性仍有待提高,在间接光照和降噪效果上都显得比较初级。
因此,在本系列的第三篇文章中,我们将把重点放在更深入的光传输建模与材质表现上:结合蒙特卡洛方法、重要性采样策略以及 GGX 微表面模型,逐步提升渲染器的物理真实性与视觉品质。