引子
最近因为身体原因,笔者暂时从深度学习前线的“填线大军”里退下来,回到家中休养。平时难得的闲暇,现在倒是意外充裕,有些无聊。人一旦无所事事,总爱翻翻过去的记忆,我才想起自己曾经还有写博客的习惯。
于是,我开始挑以前的文章,打算搬到新的个人主页上。顺便也做了一个新的博客模板,好歹能动动平面设计的手,给自己找点乐子。
那些旧文章大多是生活随想或课程笔记,技术内容不多,随便翻翻也就两个系列。但我的仓库里还有几件有意思的项目。比如当年学光线追踪写的代码,渲染出来颇有模样;还有学延迟渲染时,为 Minecraft 写的光影包,花了不少力气。
趁着这段空闲,我就回顾这些项目,把过程写下来。回到工作后,如果还能坚持写博客,也算是践行一下 Work-life Balance。要是能顺便给读者带来些帮助,那就更好了。
序言
本文是《用 Taichi 学光线追踪》系列的第一篇。这个系列的灵感,来自于《Ray Tracing in One Weekend》这本小书。它的核心理念很直接:用最小的代价写出一个能跑起来的光线追踪器,让人快速看到结果,从而体会到图形学的魅力。它不追求完整的功能,却能留下清晰的架构与无限的拓展空间。
我是在 2022 年写下这些笔记的。当时 Taichi 正受到关注,作为一门高性能的 Python 语言扩展,它能够把 GPU 编程的复杂性抽象掉,却仍保留了灵活性和高效性。相比原书使用的 C++,我觉得用 Taichi 重写一遍,不仅能降低学习门槛,也能帮助我更直观地理解光线追踪中的关键步骤。
在这个系列里,我会按照当时学习的顺序,一步一步实现:从最简单的光线与几何体相交开始,逐渐加入相机、材质、光照,直到最后能渲染出带有间接光照的图像。文章的风格更接近“学习记录”而非完整教程,重点在于保留思路、方法和踩过的坑。代码力求简明直接,读者如果愿意跟着写,通常一个周末就能跑出第一张像样的图片。
当然,渲染器远远不止于此。优化、加速、更多材质与光照模型,都超出了系列第一篇文章的范围。但如果你读完之后还想继续探索,这套框架会是一个不错的起点。
对我来说,写下这些文章既是对学习过程的整理,也是对当时热情的一种纪念。如今把它们重新搬到博客上,希望它们既能帮到后来者,也能提醒自己:即便身处“填线大军”之中,也别忘了偶尔抬头看看光影。
1. 输出一张图片
代码:GitHub
既然我们打算用 Taichi 来写一个光线追踪器,那就先从最基础的程序开始。下面这段小代码会生成一张简单的彩色图片,它的作用不在于渲染效果,而在于帮助我们熟悉 Taichi 的基本使用方式:
import time
import taichi as ti
ti.init(arch=ti.gpu) # 初始化 Taichi
Vec3f = ti.types.vector(3, float) # 定义一个三维浮点向量类型
resolution = (256, 256) # 图像分辨率
image = Vec3f.field(shape=resolution) # 创建一个二维场,用来存储图像数据
@ti.kernel
def shader():
for i, j in image: # Taichi kernel 中最外层的循环会自动并行化
image[i, j] = ti.Vector([i / resolution[0], j / resolution[1], 0.0])
start_time = time.time()
shader() # 运行 kernel
print(f"Time elapsed: {time.time() - start_time:.2f}s")
ti.tools.imwrite(image, 'outputs/1_save_img.png')
运行后,你会在 outputs/ 目录下得到一张 PNG 图片,像是一个从左下角到右上角的彩色渐变:

逐行解释
-
初始化 Taichi
ti.init(arch=ti.gpu)这里声明我们打算使用 GPU 作为计算后端。如果你没有独立显卡,改成
arch=ti.cpu也可以正常运行。 -
类型定义
Vec3f = ti.types.vector(3, float)Taichi 允许我们定义自定向量/矩阵,或者将这些基本类型组装成为结构体。这里定义了一个三维向量,用来表示 RGB 颜色(或空间中的坐标点)。
-
数据场的创建
image = Vec3f.field(shape=resolution)在 Taichi 里,数据一般存放在
field中,可以把它类比成一个数组或张量。这里的image是一个256x256的二维数组,每个元素是一个三维浮点向量。 -
编写 Kernel
@ti.kernel def shader(): for i, j in image: image[i, j] = ti.Vector([i / resolution[0], j / resolution[1], 0.0])使用
@ti.kernel修饰的函数会被 JIT 编译成高效的并行代码。在for i, j in image中,循环遍历了image的所有像素点。但与 Python 不同,Taichi kernel 中最外层的循环会被编译器自动并行化,实际运行时每个(i, j)都可以在 GPU 的一个线程中同时计算。这就是 Taichi 的强大之处:写出来像 Python 的 for 循环,跑起来却能充分利用硬件并行。 -
运行与计时
start_time = time.time() shader() print(f"Time elapsed: {time.time() - start_time:.2f}s")调用 kernel 后,我们可以看到程序运行时间。即使分辨率扩大十倍,GPU 也能轻松处理。
-
保存结果
ti.tools.imwrite(image, 'outputs/1_save_img.png')Taichi 内置了工具方法
imwrite,可以方便地把field保存成 PNG 图片。
通过这个最小的例子,我们已经接触到了 Taichi 的核心要素:
- 类型定义:用
ti.types构建向量/矩阵。 - 数据场 (field):用来存储大规模数据,支持 GPU 并行访问。
- Kernel:使用
@ti.kernel装饰器编写计算函数,自动并行执行。
理解这些之后,我们就有了写光线追踪器的最小框架。后续章节,我们会在这个框架上逐步加入更多功能。
2. 相机与射线
代码:GitHub
在上一章,我们通过一个最小示例了解了 Taichi 的基本类型、field、kernel 以及并行执行。 接下来,我们要引入光线追踪最核心的概念之一——相机和射线。在渲染中,相机决定了我们从哪看世界,而射线是从相机发出的“光线”,沿着这些光线去采样场景。
2.1 数据类型(dtype)的定义
为了在 Taichi 中方便管理向量和结构体,我们单独定义了数据类型 Vec3f、Mat3f 以及 Ray:
Vec3f = ti.types.vector(3, float)
Mat3f = ti.types.matrix(3, 3, float)
Ray = ti.types.struct(ro=Vec3f, rd=Vec3f)
Vec3f用于表示三维向量,既可表示颜色,也可表示空间坐标或方向。Mat3f用于表示 3×3 矩阵,方便旋转等变换。Ray结构体包含ro(射线原点)和rd(射线方向),是光线追踪的核心数据结构。
2.2 相机类的实现
这里我们单独实现一个 camera.py 文件用来存放相机相关的函数和类。
首先需要实现的是一个生成旋转矩阵的函数 rotate,它接收 yaw、pitch、roll 三个参数,返回一个旋转矩阵。后续会被用来执行相机空间到世界空间的转换。这个函数使用 @ti.func 修饰,使得它会被 Taichi 编译并能够被 Taichi kernel 调用。
@ti.func
def rotate(yaw, pitch, roll=0):
yaw = ti.math.radians(yaw)
pitch = ti.math.radians(pitch)
roll = ti.math.radians(roll)
yaw_trans = Mat3f([
[ ti.cos(yaw), 0, ti.sin(yaw)],
[ 0, 1, 0],
[-ti.sin(yaw), 0, ti.cos(yaw)],
])
pitch_trans = Mat3f([
[1, 0, 0],
[0, ti.cos(pitch), -ti.sin(pitch)],
[0, ti.sin(pitch), ti.cos(pitch)],
])
roll_trans = Mat3f([
[ti.cos(roll), -ti.sin(roll), 0],
[ti.sin(roll), ti.cos(roll), 0],
[ 0, 0, 1],
])
return yaw_trans @ pitch_trans @ roll_trans
相机类负责生成一张图像中每个像素对应的射线。我们用 @ti.data_oriented 修饰类,使得它可以与 Taichi kernel 交互。
Taichi 里的
data_oriented是一个装饰器,用来将类的数据成员(如self.position)绑定到 Taichi 内存管理系统,从而可以将类的成员函数定义为 Taichi kernel 或者 func
其中的核心方法是 get_rays 方法,它生成每个像素对应的射线。
@ti.data_oriented
class Camera:
def __init__(self, resolution, fov=60):
self.resolution = resolution
self.fov = float(fov)
self.position = Vec3f(0)
self.yaw = 0.0
self.pitch = 0.0
self.roll = 0.0
@ti.kernel
def get_rays(self, rays: ti.template()):
width = self.resolution[0]
height = self.resolution[1]
x, y, z = self.position
trans = rotate(self.yaw, self.pitch, self.roll)
ratio = height / width
view_width = 2 * ti.tan(ti.math.radians(self.fov) / 2)
view_height = view_width * ratio
direction = trans @ Vec3f([0.0, 0.0, -1.0])
width_axis = trans @ Vec3f([view_width, 0.0, 0.0])
height_axis = trans @ Vec3f([0.0, view_height, 0.0])
for i, j in rays:
rays[i, j].ro = [x, y, z]
rays[i, j].rd = (direction +
(i / (width - 1) - 0.5) * width_axis +
(j / (height - 1) - 0.5) * height_axis).normalized()
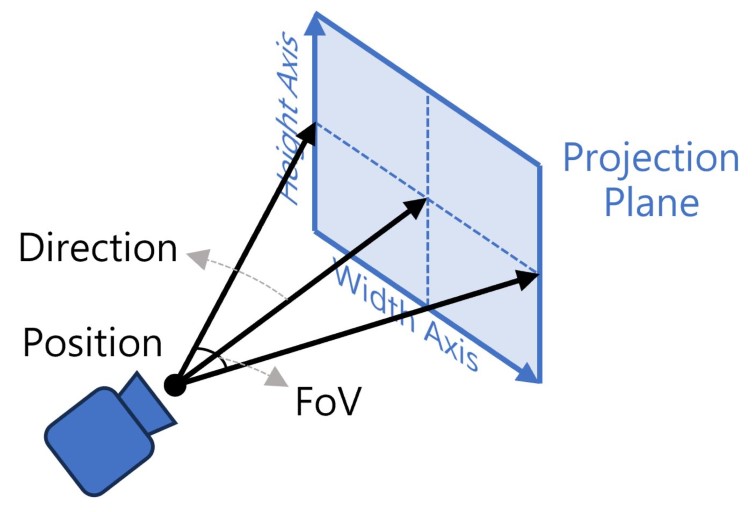
在三维空间中,相机拥有位置,方向和视场(FOV)等属性,它们共同定义了相机可见的世界范围。在光线追踪中,我们可以把相机想象成一个一个原点和投影平面:每个像素对应一条射线,这些射线从相机原点出发,穿过投影平面,进入场景:
相机属性
- 相机位置(Position):
self.position保存了相机在世界坐标系中的位置,是射线的起点。 - 相机朝向(Yaw / Pitch / Roll): 相机朝向用三个角度控制:
- Yaw:绕世界 y 轴旋转,相当于左右摇头
- Pitch:绕相机的 x 轴旋转,相当于上下点头
- Roll:绕相机的 z 轴旋转,相当于侧倾
在代码中,通过旋转矩阵
rotate(yaw, pitch, roll)将这些角度转换为一个 3×3 矩阵trans,用于把相机坐标系中的射线方向转换到世界坐标系:trans = rotate(self.yaw, self.pitch, self.roll) direction = trans @ Vec3f([0.0, 0.0, -1.0])这里
[0, 0, -1]是相机本地坐标系中的前方向。通过矩阵乘法得到世界空间方向。 - 视场(Field of View):视场决定了投影平面的大小。
view_width = 2 * ti.tan(ti.math.radians(self.fov) / 2) view_height = view_width * ratiofov为水平视场角(度),控制“镜头广角”ratio是图像高宽比view_width和view_height定义了投影平面的尺寸 在光线追踪中,每个像素都映射到投影平面上的一个点,然后由相机原点发出射线穿过这个点。
射线生成
在 get_rays kernel 中,我们遍历每个像素 (i, j),计算它对应的射线方向:
rays[i, j].rd = (direction +
(i / (width - 1) - 0.5) * width_axis +
(j / (height - 1) - 0.5) * height_axis).normalized()
direction是相机原点指向投影平面中心的向量width_axis和height_axis是投影平面的 x、y 方向向量(i / (width-1) - 0.5)和(j / (height-1) - 0.5)将像素索引映射到[-0.5, 0.5]normalized()保证射线方向是单位向量
最终,每条射线包含两个信息:
ro:射线原点(相机位置)rd:射线方向(单位向量,指向投影平面像素)
2.3 基础 shader
我们先实现一个非常简单的 shader,让每条射线根据 y 方向线性插值生成颜色,从而形成一个渐变背景:
@ti.func
def ray_color(ray):
t = 0.5*(ray.rd[1] + 1.0)
return (1.0-t)*Vec3f([1.0, 1.0, 1.0]) + t*Vec3f([0.5, 0.7, 1.0])
@ti.kernel
def shader(rays: ti.template()):
for i, j in image:
image[i, j] = ray_color(rays[i, j])
ray_color将射线方向映射到颜色,得到类似天空渐变效果。shaderkernel 遍历整个图像,将每条射线的颜色写入image。
2.4 组合运行
完整的执行流程如下:
ti.init(arch=ti.gpu)
resolution = (1280, 720)
image = Vec3f.field(shape=resolution)
rays = Ray.field(shape=resolution)
camera = Camera(resolution)
camera.set_direction(0, 30, 0)
camera.get_rays(rays)
import time
start_time = time.time()
shader(rays)
print(f"Time elapsed: {time.time() - start_time:.2f}s")
ti.tools.imwrite(image, 'outputs/2_camera_and_ray.png')
运行后,你将得到一张从下到上的天空渐变图像:

3. 添加一个球
代码:GitHub
在上一章,我们实现了基础的相机和射线生成,并通过 ray_color shader 渲染了一张简单的天空渐变图。现在,我们来为场景添加一个球体,这是光线追踪最经典的几何体之一,也是理解射线与几何体相交的起点。
3.1 射线与球的相交
光线追踪的核心之一,就是计算射线与物体的交点。对于球体,可以用解析公式快速求解:
\[\| \mathbf{o} + t \mathbf{d} - \mathbf{c} \|^2 = r^2\]这里:
- $\mathbf{o}$ 是射线原点
- $\mathbf{d}$ 是射线方向(单位向量)
- $\mathbf{c}$ 是球心
- $r$ 是球半径
- $t$ 是沿射线的参数,表示交点的位置
求解该二次方程即可得到交点 t。
在 Taichi 中,我们实现了 hit_sphere 函数:
@ti.func
def hit_sphere(center, radius, ray):
oc = ray.ro - center
a = 1
b = 2.0 * ti.math.dot(oc, ray.rd)
c = ti.math.dot(oc, oc) - radius**2
discriminant = b**2 - 4 * a * c
res = -1.0
if discriminant >= 0:
res = (-b - ti.sqrt(discriminant)) / (2.0 * a)
return res
oc = ray.ro - center:射线原点到球心的向量discriminant:判别式,判断是否有交点- 若有交点,返回最小的根
t,否则返回-1表示射线未击中球
注意:
- 这里
a = 1,因为射线方向已经是单位向量,简化了计算。- 若射线的出发点在球体内部,则得到的
t可能是负数,这会被之后的逻辑处理掉。如果我们不考虑光线在球体内部的情况,比如场景内并没有透明物体,就没有问题;否则,需要额外的判断。
3.2 更新 ray_color
在添加球体之后,我们的 ray_color 需要根据射线是否击中球体来决定颜色:
@ti.func
def ray_color(ray):
center = Vec3f([0, 0, -2]) # 球放置在相机正前方 2m 的位置
radius = 0.5 # 球半径为 0.5m
color = Vec3f(0.0)
t = hit_sphere(center, radius, ray)
if t > 0:
normal = (ray.ro + t * ray.rd - center).normalized()
color = 0.5 * (normal + 1)
else:
t = 0.5*(ray.rd[1] + 1.0)
color = (1.0-t)*Vec3f([1.0, 1.0, 1.0]) + t*Vec3f([0.5, 0.7, 1.0])
return color
- 如果射线击中球体,我们计算球面法线
normal并将其映射到[0,1]范围,用作颜色显示 - 如果射线未击中球体,则沿用天空渐变背景
这种方式可以快速看到球体的形状和法线方向效果,作为一个简单的可视化。
3.3 Kernel 与渲染
Kernel 与之前相同,只是将 ray_color 更新为新的版本:
@ti.kernel
def shader(rays: ti.template()):
for i, j in image:
image[i, j] = ray_color(rays[i, j])
调用流程保持不变:
camera = Camera(resolution)
camera.set_direction(0, 0)
camera.get_rays(rays)
start_time = time.time()
shader(rays)
print(f"Time elapsed: {time.time() - start_time:.2f}s")
ti.tools.imwrite(image, 'outputs/3_adding_a_sphere.png')
运行后,你会看到一张包含球体的图像,球体颜色由法线决定,背景依旧是渐变天空:

4. 多几何体
代码:GitHub
到现在为止,我们已经完成了基础 Taichi 使用、相机与射线生成,以及渲染单个球体。现实场景往往包含多个物体,所以接下来,我们要扩展渲染器,让它能够处理多个球体。
4.1 记录击中信息:HitRecord
每条射线可能会击中场景中的物体。为了统一管理,我们定义一个结构体来记录击中信息:
HitRecord = ti.types.struct(
point=Vec3f, # 交点坐标
normal=Vec3f, # 法向量
t=ti.f32 # 射线参数 t
)
这里 t 表示交点在射线上的位置,如果 t < 0 就说明没有击中物体。
这种设计方便我们在 shader 中直接使用击中点信息计算颜色和光照。
4.2 封装球体:Sphere 类
球体是最简单也是最经典的几何体。我们把球体的属性和求交方法封装在一个类里:
这里所用的装饰器
@ti.dataclass用于将 Python 类声明为 Taichi 可识别的数据结构。它会自动为类的每个字段分配 GPU/CPU 内存,并允许在 Taichi kernel 或@ti.func中直接访问。这等价于在 Taichi 中定义一个结构体ti.types.struct,但在书写更加 Pythonic,特别是需要定义成员函数的情况下。详见 Taichi Dataclass
@ti.dataclass
class Sphere:
center: Vec3f
radius: ti.f32
@ti.func
def hit(self, ray):
oc = ray.ro - self.center
a = 1.0
b = 2.0 * ti.math.dot(oc, ray.rd)
c = ti.math.dot(oc, oc) - self.radius**2
discriminant = b**2 - 4*a*c
record = HitRecord(0.0)
record.t = -1
if discriminant >= 0:
record.t = (-b - ti.sqrt(discriminant)) / (2*a)
record.point = ray.ro + record.t * ray.rd
record.normal = (record.point - self.center).normalized()
return record
说明:
- 射线方向已经归一化,所以
a = 1 - 判别式
discriminant用于判断是否有交点 - 如果有交点,返回最近交点
t、交点坐标和法向量
4.3 管理场景:World 类
在上一节中,我们为球体编写了 hit 方法,使得射线能够与单个球体求交。可是现实的场景往往包含不止一个物体。如果在 shader 里直接把所有球体的求交逻辑写死,会让代码变得又长又乱,也不利于后续扩展。
因此,我们需要一个统一的接口:把场景中的所有几何体收集到一起,并对外暴露一个 hit(ray) 方法,用来返回射线与整个场景中最近的击中点。
这里我们定义了一个 World 类,专门负责管理场景。
@ti.data_oriented
class World:
def __init__(self, spheres=[]):
self.capacity = max(len(spheres), 16) # 初始容量
self.size = len(spheres) # 当前球体数量
self.spheres = Sphere.field(shape=(self.capacity,))
for i in range(self.size):
self.spheres[i] = spheres[i]
初始化时,World 会开辟一个 Sphere.field 用来存放球体。我们使用“容量 / 已用大小”的方式管理,就像一个动态数组,可以在运行时不断扩展。
添加新球体时,如果超过容量,会自动扩展为原来两倍:
def add(self, sphere):
if self.size >= self.capacity:
self.capacity *= 2
new_spheres = Sphere.field(shape=(self.capacity,))
for i in range(self.size):
new_spheres[i] = self.spheres[i]
self.spheres = new_spheres
self.spheres[self.size] = sphere
self.size += 1
这样一来,我们就可以在 Python 端灵活地往场景里添加任意数量的球体,而不需要提前知道会有多少个。
真正关键的是 hit 方法:
@ti.func
def hit(self, ray):
res = HitRecord(0.0)
res.t = -1
for i in range(self.size):
record = self.spheres[i].hit(ray)
if record.t >= 1e-4 and (res.t < 0 or record.t < res.t):
res = record
return res
这里我们遍历所有球体,调用它们各自的 hit(ray) 方法,并保留最近的交点(即 t 最小的那个)。1e-4 用来避免浮点误差导致的“自相交”。
通过 World.hit(ray),在 shader 中,射线不需要知道场景里有多少物体,也不需要遍历每个物体的逻辑。这样做让渲染器的核心算法和场景管理完全解耦。
4.4 shader:渲染整个场景
在 shader 中,我们调用 World.hit(ray) 获取最近击中点,然后根据击中情况计算颜色:
@ti.func
def ray_color(ray, world: ti.template()):
hit = world.hit(ray)
color = Vec3f(0.0)
if hit.t >= 0:
# 用法线做简单着色
color = 0.5 * (hit.normal + 1)
else:
# 天空渐变
t = 0.5*(ray.rd[1] + 1.0)
color = (1.0-t)*Vec3f([1.0,1.0,1.0]) + t*Vec3f([0.5,0.7,1.0])
return color
@ti.kernel
def shader(world: ti.template(), rays: ti.template()):
for i, j in image:
image[i, j] = ray_color(rays[i, j], world)
- 如果击中球体,用法线映射到
[0,1]作为颜色 - 如果未击中,用 y 方向线性插值生成天空渐变
4.5 完整运行示例
import time
import taichi as ti
from dtypes import Vec3f, Ray
from camera import Camera
from world import World, Sphere
ti.init(arch=ti.gpu)
resolution = (1280, 720)
image = Vec3f.field(shape=resolution)
rays = Ray.field(shape=resolution)
camera = Camera(resolution)
camera.set_direction(0,0)
camera.set_position(Vec3f([0,0,3]))
camera.get_rays(rays)
# 场景:一个球 + 地面
sphere = Sphere(Vec3f([0,0,0]), 0.5)
ground = Sphere(Vec3f([0,-100.5,0]), 100)
world = World([sphere, ground])
start_time = time.time()
shader(world, rays)
print(f"Time elapsed: {time.time() - start_time:.2f}s")
ti.tools.imwrite(image, 'outputs/4_objects.png')
运行后,你会得到一张包含球体和地面的图像:

5. 抗锯齿与多重采样
代码:GitHub
到目前为止,我们的渲染器能绘制多个球体,也能根据法线或者背景颜色着色。可是你可能已经注意到了:当我们把分辨率调低时,球体边缘会出现明显的“锯齿”。这是因为我们每个像素只采样一次,导致边界处的像素要么全是球体颜色,要么全是背景颜色,看起来非常生硬。

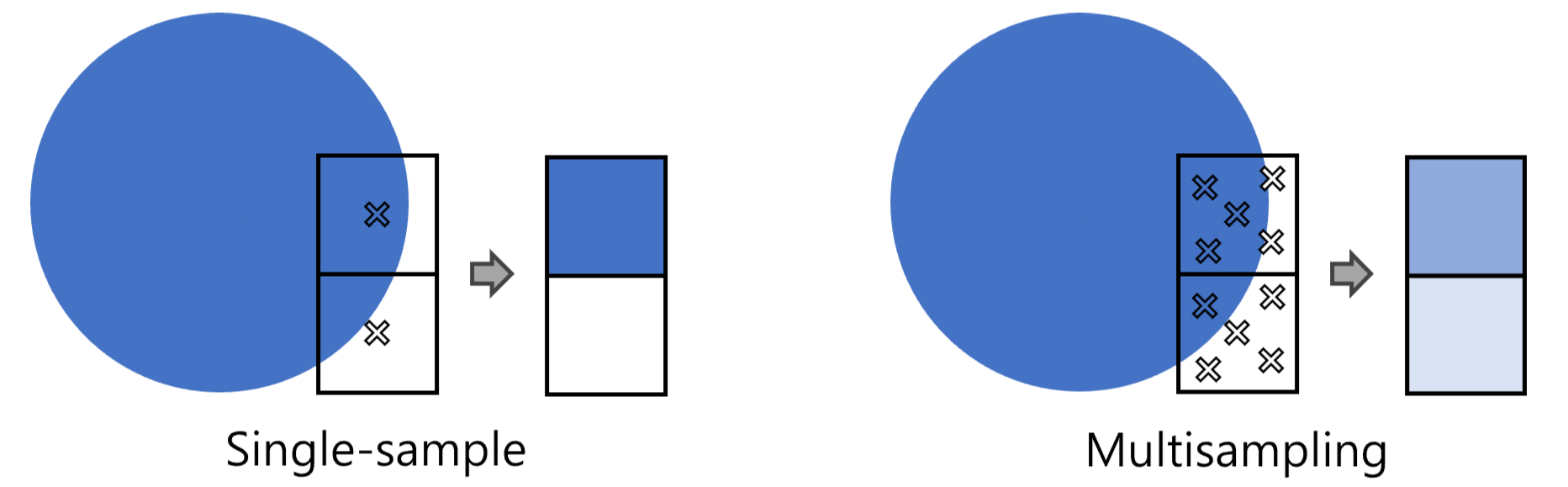
一种解决办法是:抗锯齿(Anti-aliasing)。在光线追踪里,最简单的抗锯齿方案就是多重采样(Multisampling):每个像素不是只发一条射线,而是发多条,落在像素内部的随机位置上,然后取平均。
5.1 为什么需要多重采样?
举个例子,如果一个像素刚好覆盖了球体的一部分,真实情况应该是:这个像素有一部分面积属于球体,另一部分属于背景。可如果我们只发一条射线,就只能看到“是”或者“否”,缺失了“部分覆盖”的信息。
通过多重采样,我们就能更真实地统计像素内的覆盖比例,让边缘自然过渡:
- 单次采样(1 sample): 只有硬边
- 多重采样(>10 samples): 边缘平滑,过渡柔和
这就是光线追踪版的“抗锯齿”。
5.2 修改相机的 get_rays 实现随机采样
Taichi 提供了 ti.random() 函数,可以在 [0, 1) 范围生成随机数。我们只需要在像素坐标 (i, j) 的基础上加上一个小的随机偏移,就能得到每个像素范围内均匀分布的随机采样位置:
@ti.kernel
def get_rays(self, rays: ti.template()):
width = self.resolution[0]
height = self.resolution[1]
x = self.position[0]
y = self.position[1]
z = self.position[2]
trans = rotate(self.yaw, self.pitch, self.roll)
ratio = height / width
view_width = 2 * ti.tan(ti.math.radians(self.fov) / 2)
view_height = view_width * ratio
direction = trans @ Vec3f([0.0, 0.0, -1.0])
width_axis = trans @ Vec3f([view_width, 0.0, 0.0])
height_axis = trans @ Vec3f([0.0, view_height, 0.0])
for i, j in rays:
rays[i, j].ro = [x, y, z]
- rays[i, j].rd = (direction + (i / (width - 1) - 0.5) * width_axis + (j / (height - 1) - 0.5) * height_axis).normalized()
+ rays[i, j].rd = (direction + ((i + ti.random(ti.f32)) / width - 0.5) * width_axis + ((j + ti.random(ti.f32)) / height - 0.5) * height_axis).normalized()
5.3 多重采样 shader
现在我们修改 shader,让每个像素采样多次。比如每个像素采样 100 次,然后取平均值:
spp = 100
@ti.kernel
def shader(world: ti.template(), rays: ti.template()):
for i, j in rays:
image[i, j] += ray_color(rays[i, j], world) / spp
def render(world: World, camera: Camera):
for _ in trange(spp):
camera.get_rays(rays)
shader(world, rays)
关键点:
- 多次调用
camera.get_ray(rays)发射射线 - 将所有结果累加,最后除以采样次数,得到平均颜色
5.4 渲染效果
运行后,你会发现球体的边缘明显更平滑,锯齿几乎消失了。随着 spp 增加,结果会越来越接近真实情况,但渲染时间也会相应增长。


6. 光照:漫反射
代码:GitHub
到目前为止,我们的画面已经能显示一个球,能区分前景和背景。但这幅图像依旧显得单薄:球体像是贴在纸上的一个圆,没有体积感,也没有光影。真正让三维世界鲜活起来的,是光照。
光照计算的引入,意味着我们不能再满足于“击中即返回一种固定颜色”的逻辑。相反,光线击中物体后,要根据表面的法线方向、材质属性、以及新的散射方向,进行多次弹射,决定最终的颜色。这一转变,需要我们对代码实现进行一些准备。
6.1 反照率(Albedo)
在光照计算中,球体表面本身的颜色就是一个非常重要的属性,我们称之为 反照率(albedo)。它决定了表面在接受光照后,能够反射出多少以及哪种颜色的光。
在前几章中,球体的颜色是根据法线映射得出的,这只是为了可视化法线方向,实际上并没有体现真实材质的光照效果。现在,我们要让每个球体拥有自己的 albedo,这样射线击中球体时,颜色就会受到材质本身的影响。
修改 Sphere 类,增加 albedo 属性:
@ti.dataclass
class Sphere:
center: Vec3f
radius: ti.f32
albedo: Vec3f
@ti.func
def hit(self, ray):
oc = ray.ro - self.center
a = 1
b = 2.0 * ti.math.dot(oc, ray.rd)
c = ti.math.dot(oc, oc) - self.radius**2
discriminant = b**2 - 4 * a * c
record = HitRecord(0.0)
record.t = -1
if discriminant >= 0:
record.t = (-b - ti.sqrt(discriminant)) / (2.0 * a)
record.point = ray.ro + record.t * ray.rd
record.normal = (record.point - self.center).normalized()
record.albedo = self.albedo
return record
这里我们给 HitRecord 增加了一个 albedo 字段,用来存储击中点的材质颜色。
HitRecord = ti.types.struct(point=Vec3f, normal=Vec3f, t=ti.f32, albedo=Vec3f)
6.2 漫反射 BSDF
在自然界中,光线与物体表面相互作用时,其强度和传播方向都会发生改变,宏观表现为吸收、散射、反射和折射等现象。
为了在光线追踪中建模这些过程,每一次光线与物体表面相交时,下一步的方向与能量分布都由 BSDF(Bidirectional Scattering Distribution Function,双向散射分布函数)决定。它描述了 光从某一方向入射到表面后,以另一方向散射出的概率与强度。
在这一节里,我们先从最简单的一种 BSDF——漫反射(Lambertian)开始。
对于理想的漫反射表面,光线以各个方向散射的概率是均匀的,它只与表面法线相关,而与入射光方向无关。换句话说,当一条光线射到一个漫反射球体上时,它的出射方向可以看作是法向半球上的一个随机方向。
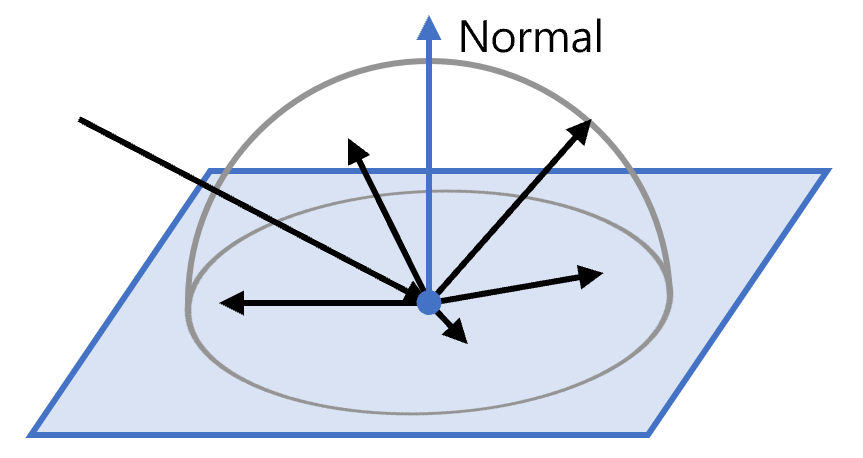
但是,当我们实际对漫反射表面进行路径追踪时,更好的选择是通过 余弦加权采样(cosine-weighted sampling) 来确定出射方向。
这是因为,对于我们考虑的射线与场景的相交点,虽然各个方向的入射光会以相同的概率散射到观察方向,但不同方向的入射光带来的贡献是不同的。相同光强下,与法向有更大的角度的入射光,其对亮度的贡献更低,遵循 $(\mathbf{n}\cdot \omega_i)$ 的余弦因子。
读者可以发挥一下想象力:入射方向与表面法线夹角越大,光线照射在单位面积上的投影越小,也就是“摊薄”在更大的一块区域上。因此,即便入射光本身强度相同,斜射光对表面的能量贡献也会更弱。
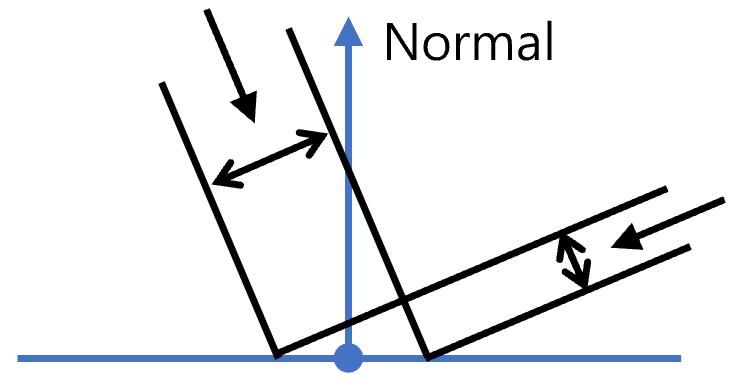
如果我们在采样时直接按余弦分布来生成方向,那么这个余弦项会和采样概率密度函数(PDF)相抵消,使得积分估计更加高效,方差更小。这称之为 重要性采样(Importance Sampling)。
换句话说:
- 均匀采样半球:所有方向等概率,但会导致一些贡献大的方向(接近法线)采样不足。
- 余弦加权采样:更偏向于法线方向采样,符合物理规律,同时提升收敛速度。
我们新建一个 DiffuseBSDF 类,用来实现漫反射情况下,光线与物体表面相交时的交互逻辑:
@ti.func
def _sample_at_sphere():
z = 1 - 2 * ti.random(ti.f32)
r = ti.sqrt(1 - z**2)
theta = 2 * ti.math.pi * ti.random(ti.f32)
x = r * ti.cos(theta)
y = r * ti.sin(theta)
return Vec3f([x, y, z])
@ti.func
def _sample_lambertian(normal):
s = _sample_at_sphere()
return (normal + s).normalized()
class DiffuseBSDF:
@staticmethod
@ti.func
def sample(ray: ti.template(), hit: ti.template()):
ray.l *= hit.albedo
ray.ro = hit.point
ray.rd = _sample_lambertian(hit.normal)
上面的代码使用了一种特别的方案来进行余弦加权采样:
- 先在单位球面上随机采样一个方向
s - 然后将
s和法线方向相加,得到一个新的方向d - 最后将
d归一化,得到最终的散射方向。
其数学原理并不太直观,接下来我们用图示的方式来证明:
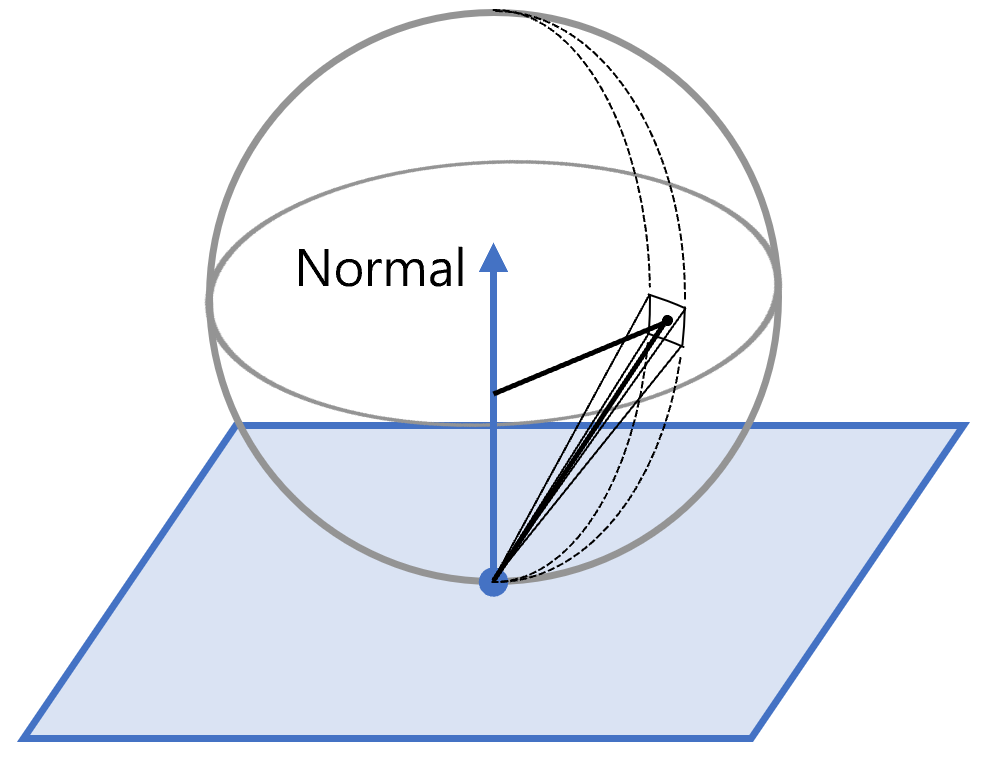
图中展示了一个可能的散射方向对应的立体角微元,以及其在大球上的投影微元。因为采样在大球的球面上是均匀的,所以散射方向落在该立体角微元的概率正比于球面上投影微元的面积。
在极坐标系下,设该散射方向的坐标为 $(\theta, \phi)$,分别表示与法线的夹角和水平偏转角。设立体角微元对应的角度微元为 $\mathrm{d}\theta$ 和 $\mathrm{d}\phi$,则立体角微元的大小和投影微元的面积分别为
- 立体角微元大小: 易知为 $\sin\theta\cdot\mathrm{d}\theta\cdot\mathrm{d}\phi$
- 投影微元面积:
- 经线方向的长度为(圆周角定理): $2\mathrm{d}\theta$
- 纬线方向的长度为: $\sin\theta\cdot\cos\theta\cdot\mathrm{d}\phi$
- 面积为: $2\sin\theta\cdot\cos\theta\cdot\mathrm{d}\theta\cdot\mathrm{d}\phi$
二者之比即为未归一化的概率密度函数(PDF),即:
\[\frac{2\sin\theta\cdot\cos\theta\cdot\mathrm{d}\theta\cdot\mathrm{d}\phi}{\sin\theta\cdot\mathrm{d}\theta\cdot\mathrm{d}\phi} = 2\cos\theta\]发现概率密度正比于 $\cos\theta$,满足余弦加权采样的要求。
最后看 DiffuseBSDF.sample:
class DiffuseBSDF:
@staticmethod
@ti.func
def sample(ray: ti.template(), hit: ti.template()):
ray.l *= hit.albedo
ray.ro = hit.point
ray.rd = _sample_lambertian(hit.normal)
这一段逻辑可以拆解为:
- 能量衰减
ray.l *= hit.albedo光线击中物体后,能量会被材质吸收一部分,只保留对应反照率的成分。 - 更新光线位置
ray.ro = hit.point光线新的起点就是交点位置。 - 更新光线方向
ray.rd = _sample_lambertian(hit.normal)使用余弦加权采样,生成新的散射方向。
这样,每次光线击中漫反射材质时,我们就能根据 BSDF 的定义更新光线,继续路径追踪。
6.3 路径跟踪(Path Tracing)
在理解了漫反射表面的基本行为后,我们就可以进一步考虑光线在场景中的完整传播过程。光线击中物体表面时不再只是返回一个固定颜色,而是会继续沿新的方向传播。现实世界中的光往往在一次次的碰撞与散射中逐渐损失能量,直到最终进入人眼。为了更好地贴近这种物理过程,我们需要让光线在与球体相交后“继续走下去”。
这就是 路径跟踪(Path Tracing) 的基本思想:
- 光线从摄像机发出,击中物体表面。
- 根据表面法线与材质性质,计算一个新的散射方向。
- 沿着新方向继续发射光线,直到击中背景或达到递归深度。
- 在每一次散射过程中,将光线的能量按照材质反照率(albedo)进行衰减。
这首先需要我们存储每条光线在路径跟踪执行过程中的过程量:
- 累积的反照率衰减值: 每一次散射,光线的能量都会受到材质反照率的影响,我们需要记录衰减值,以便在最后计算颜色时进行衰减。
- 是否击中背景: 光线在递归过程中,有可能会一直往前走,直到没有更多的交点,这时我们需要判断是否击中了背景,用来终止递归。
我们在 Ray 结构中增加字段,用来存储这些量:
Ray = ti.types.struct(ro=Vec3f, rd=Vec3f, l=Vec3f, end=ti.int8)
别忘了在 Camera.get_rays 中初始化 Ray 结构:
rays[i, j].l = Vec3f([1.0, 1.0, 1.0])
rays[i, j].end = 0
接下来,我们需要实现路径跟踪的核心逻辑。整体思路是:光线在场景中不断传播、散射,直到遇到背景或者达到最大递归深度。在这个过程中,我们累积每次散射后的能量衰减,并在光线结束时,将结果写入最终图像。
在代码中,这一逻辑主要体现在以下几个函数:
-
propagate_once@ti.func def propagate_once(ray: ti.template(), world: ti.template()): if ray.end == 0: hit = world.hit(ray) if hit.t >= 0: DiffuseBSDF.sample(ray, hit) else: ray.end = ti.int8(1)这个函数表示“光线传播一步”。
- 如果光线击中物体,则调用
DiffuseBSDF.sample计算新的方向,并更新能量。 - 如果没有击中任何物体,说明光线“走到头了”,需要标记为结束状态。
- 如果光线击中物体,则调用
-
shaderspp = 8192 propagate_limit = 32 @ti.func def backbround_color(ray): t = 0.5*(ray.rd[1] + 1.0) color = (1.0-t)*Vec3f([1.0, 1.0, 1.0]) + t*Vec3f([0.5, 0.7, 1.0]) return color @ti.kernel def shader(world: ti.template(), rays: ti.template()): for i, j in rays: ray = rays[i, j] for _ in range(propagate_limit): propagate_once(ray, world) if ray.end == 1: break if ray.end == 1: image[i, j] += backbround_color(ray) * ray.l / spp这是路径跟踪的主循环。
- 每条光线在进入场景后,会执行最多
propagate_limit次传播。 - 如果在传播过程中遇到背景,就提前结束。
- 最终根据光线是否击中背景,计算并累积像素的颜色。
- 每条光线在进入场景后,会执行最多
6.4 运行示例
camera = Camera(resolution)
camera.set_direction(0, 0)
camera.set_position(Vec3f([0, 0, 4]))
sphere1 = Sphere(Vec3f([0.0,0.0,0.0]), 0.5, Vec3f([0.25, 0.25, 0.5]))
sphere2 = Sphere(Vec3f([-1.0,0.0,0.0]), 0.5, Vec3f([0.25, 0.5, 0.25]))
sphere3 = Sphere(Vec3f([1.0,0.0,0.0]), 0.5, Vec3f([0.5, 0.25, 0.25]))
ground = Sphere(Vec3f([0,-10000.5,0.0]), 10000, Vec3f([0.25, 0.25, 0.25]))
world = World([sphere1, sphere2, sphere3, ground])
start_time = time.time()
render(world, camera)
print(f"Time elapsed: {time.time() - start_time:.2f}s")
ti.tools.imwrite(image, 'outputs/6_diffuse.png')
场景由地面和红绿蓝三色球体组成,运行上面的代码,你会得到这样的一幅画面:

相比之前的“固定颜色”或者“单次反射”结果,现在的画面已经出现了更自然的光影层次,球体之间互相影响,地面也显得更真实。虽然还比较粗糙,但这就是路径追踪的雏形。
6.5 色调映射(Tone Mapping)和 Gamma 矫正
观察上面得到的图像可以发现,经过路径追踪渲染的原始结果往往偏暗,光影层次也不够真实。
这是因为路径追踪输出的是线性的物理光强,而显示器和人眼对亮度的感知都是非线性的。为了让画面更符合视觉习惯,我们需要对渲染结果进行色调映射(Tone Mapping)和Gamma 矫正,将其转换到 sRGB 空间。
这部分代码位于
postprocess.py文件中,具体实现请参考源码。
色调映射(Tone Mapping)
路径追踪输出的是物理上的线性光强(linear HDR),范围为 $[0, +\infty)$。它可能包含比显示器可显示范围 $[0,1]$ 更亮或者更暗的光照值。如果直接显示,结果往往会显得过暗或局部过曝,丢失很多细节。
色调映射的作用就是将高动态范围的亮度压缩到可显示范围,同时尽量保留亮部和暗部细节,让画面看起来更自然。它有几种常见方式:
- 线性缩放:直接按最大亮度将像素值缩放到 $[0,1]$。简单但容易导致亮部压扁、暗部细节不足。
- Reinhard 映射:常用公式
L_d = L / (1 + L),可以平滑压缩高亮区域,同时保留中低亮度细节。 - Filmic Tone Mapping:所谓的“电影”色调映射算子旨在模拟真实的胶片色调,可以保留更多细节。
通过色调映射,原本过亮或过暗的区域可以被合理“映射”到显示器范围,让画面光影层次更丰富。
这里我们使用 ACES 色调映射,它属于 Filmic Tone Mappig 系:
@ti.func
def ACES_tonemapping(color):
aces_input_matrix = Mat3f([
[0.59719, 0.35458, 0.04823],
[0.07600, 0.90834, 0.01566],
[0.02840, 0.13383, 0.83777]
])
aces_output_matrix = Mat3f([
[1.60475, -0.53108, -0.07367],
[-0.10208, 1.10813, -0.00605],
[-0.00327, -0.07276, 1.07602]
])
v = aces_input_matrix @ color
a = v * (v + 0.0245786) - 0.000090537
b = v * (0.983729 * v + 0.4329510) + 0.238081
v = a / b
return ti.math.max(aces_output_matrix @ v, 0.0)
关于色调映射的更多内容,可以参考这一篇非常详细的介绍文章 Tone Mapping | δelta。
Gamma 矫正
即使进行了色调映射,图像仍然是线性的光强(linear RGB)。然而,人眼对亮度的感知是非线性的:我们对暗部的亮度变化比亮部更敏感。显示器也通常假设输入的图像是非线性编码(sRGB)。
Gamma 矫正就是将线性光强转换为符合 sRGB 显示的非线性亮度值,常用公式为:
\[C_{\text{sRGB}} = C_{\text{linear}}^{1/\gamma}, \quad \gamma \approx 2.2\]其中的 $\gamma$ 就是 Gamma 值,对于一般显示器,$\gamma$ 通常取 2.2。
作用如下:
- 匹配人眼感知:暗部更容易分辨亮度差异,亮部不过曝。
- 适应显示器:现代显示器假设输入是 gamma 编码后的图像,如果直接显示线性光强,图像会偏暗。
经过 Gamma 矫正后,图像的亮度看起来更自然,细节更丰富,整体效果更加贴近人眼所见。
@ti.func
def gamma_correction(color, gamma):
return color**(1/gamma)
添加后处理
我们将前面实现的色调映射和 Gamma 矫正函数封装成一个函数 postprocess,并在 render 函数中调用:
@ti.kernel
def post_processing():
for i, j in image:
c = image[i, j]
c = ACES_tonemapping(c)
c = gamma_correction(c, 2.2)
image[i, j] = c
def render(world: World, camera: Camera):
for _ in trange(spp):
camera.get_rays(rays)
shader(world, rays)
post_processing()
运行修改后的代码,你会得到这样的渲染结果:


7. 光照:一般反射
代码:GitHub
在上一章中,我们实现了漫反射(Lambertian)材质和路径追踪,使场景中的球体拥有了自然的光影层次。虽然效果已经比单次反射逼真许多,但现实世界的材质远不止漫反射。金属、陶瓷、塑料等物体会呈现出镜面反射和高光,这就需要引入一般反射模型。
7.1 PBR 材质模型
为了更接近真实物理现象,我们采用物理基础渲染(Physically Based Rendering, PBR)理念描述材质。PBR 材质通常包含以下参数:
| 参数 | 含义 |
|---|---|
| albedo | 漫反射颜色,决定物体表面对光的反照率 |
| metallic | 金属度,0 表示非金属(电介质),1 表示纯金属 |
| roughness | 粗糙度,控制反射光的扩散程度,0 表示完全镜面反射 |
| ior | 电介质材料的折射率,控制透射/漫反射光和反射光的比例 |
结合这些参数,PBR 可以统一描述从完全漫反射的塑料到高度镜面的金属的各种材质,实现物理一致且视觉逼真的光照效果。
代码层面,我们需要拓展原来只包含 albedo 的材质,定义 Material 结构,增加 PBR 材质参数:
Material = ti.types.struct(albedo=Vec3f, roughness=ti.f32, metallic=ti.i32, ior=ti.f32)
HitRecord 对应改为记录击中点的材质:
HitRecord = ti.types.struct(point=Vec3f, normal=Vec3f, t=ti.f32, material=Material)
7.2 微平面模型
在之前的漫反射一节中,我们把表面看作一个整体,并假设光线在法向半球中各向均匀散射。这种宏观模型在计算和直观理解上都很方便,但它并没有回答一个更深层的问题:
在微观尺度上,为什么光线的出射方向看似随机?
真实世界中的物体表面并不是完全光滑的平面。即便是经过抛光的金属、陶瓷或玻璃,在显微镜下也会表现为由无数微小凸起、凹陷和纹理组成的复杂地形。
对于理想光滑表面,光线严格遵循几何光学定律,入射角等于反射角,表现为完全镜面反射。那么粗糙表面可以被近似看作由许多朝向不同的微小平面(microfacets)组成。每个微平面上的反射仍然是镜面的,但由于法线分布不同,宏观上观察到的光分布就表现为“散射”。
换句话说,出射方向的随机性来自微平面法线的统计分布。
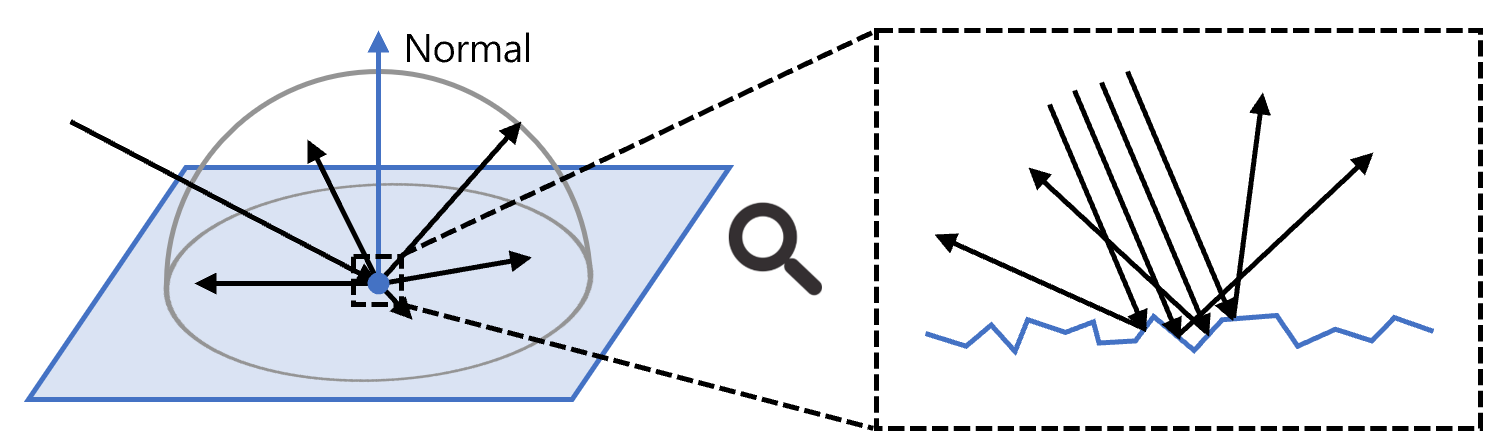
微平面模型(Microfacet Model)正是建立在这种观察上的。
微平面模型假设表面由大量微小镜面单元构成,每个单元有一个朝向随机的法线。光线射入时,会选择一个微平面与之作用,并在其法线上发生镜面反射或折射。宏观上,出射光的整体分布由这些微平面法线的概率分布函数决定。
因此,微平面模型的关键是 如何统计和描述微平面法线的分布。这由所谓的 法线分布函数(Normal Distribution Function, NDF) 来建模。
常见的分布模型包括:
- Beckmann 分布:假设表面起伏近似服从高斯分布。
- GGX / Trowbridge-Reitz 分布:现代 PBR 的主流选择,能够更好地捕捉粗糙材质中高光的长尾特性。
这些分布的范围由 PBR 参数中的粗糙度(roughness)控制,从而决定了反射的“锐利”还是“模糊”。
不过,要直接对这些分布进行采样,并结合余弦项实现重要性采样,往往比较复杂,也超出了“第一个周末”的能力范围。为了代码实现的简洁性,我们采用一种近似方案:通过在镜面反射方向与漫反射方向之间进行球面插值(slerp),来模拟粗糙度的影响。
代码解析
@ti.func
def _slerp(a, b, t):
omega = ti.acos(ti.math.clamp(a.dot(b), -1, 1))
so = ti.sin(omega)
o = (1 - t) * a + t * b if so < 1e-6 else \
(ti.sin((1 - t) * omega) / so) * a + (ti.sin(t * omega) / so) * b
return o.normalized()
slerp(spherical linear interpolation)是球面插值函数,用于在两个单位向量 a 和 b 之间平滑插值。
omega表示两向量的夹角;- 如果
omega很小,直接退化为线性插值; - 否则用正弦函数构造出均匀的球面插值,避免方向偏差。
@ti.func
def _sample_normal(dir, normal, roughness):
s = _sample_lambertian(normal)
k = -dir.dot(normal)
r = dir + 2 * k * normal
r = _slerp(r, s, roughness*roughness)
n = (r - dir).normalized()
return n
_sample_normal 的作用是根据入射方向 dir、表面法线 normal 以及粗糙度 roughness 来生成一个新的“有效法线” n:
-
s = _sample_lambertian(normal)在表面法线半球采样一个余弦加权的随机方向,代表粗糙表面可能产生的漫反射方向。 -
r = dir + 2 * k * normal计算镜面反射方向。这里k = -dir.dot(normal)表示入射光在法线方向上的投影。 -
r = _slerp(r, s, roughness*roughness)在理想镜面反射方向r和随机漫反射方向s之间插值。插值比例由roughness²控制:- 当
roughness=0时,结果接近纯粹的镜面反射。 - 当
roughness=1时,结果接近完全的漫反射。
这里使用
roughness²主要是为了便于在低粗糙度范围内提供更细腻的控制。 人眼对高光的感知在低粗糙度时非常敏感,如果直接用线性roughness作为插值因子,那么在0.0 ~ 0.2之间的变化过于剧烈。通过平方映射,能让“镜面到漫反射”的过渡更符合感知上的均匀性。 - 当
-
n = (r - dir).normalized()得到最终的“微平面法线”。这里r - dir实际上对应半程向量(half vector),即入射光与出射光的夹角方向。
最终,这个函数为每一条入射光射线生成一个与粗糙度相匹配的有效微平面法线。
7.3 菲涅尔公式
在微平面模型中,表面由无数取向各异的微小平面组成。入射光某个微平面发生相互作用时,可以近似看作与一个光滑平面的交互。
而光线与平面的交互规律在物理上已有精确描述:当光射到介质交界面时,会同时产生反射和透射两部分:
- 反射光 —— 沿着镜面方向弹回
- 透射光 —— 穿过表面进入另一介质
由于能量守恒,反射率 $F(\theta)$ 与透射率 $T(\theta)$ 必须满足:
\[F(\theta) + T(\theta) = 1\]决定两者比例关系的,正是菲涅尔公式(Fresnel Equations)。
物理上精确的菲涅尔公式较为复杂,在渲染中,我们通常使用的是它的 Schlick 近似公式:
\[F(\theta) \approx F_0 + (1 - F_0)(1 - \cos \theta)^5\]其中:
- $F_0$ 是正对表面时的物质的反射率
- $\theta$ 是入射光与法线的夹角
这说明反射比例不仅取决于物体的材质参数,还与观察角度密切相关。
- 当视线与表面法线接近时($\theta \approx 0$),反射率接近 $F_0$,也就是材质的固有反射率。
- 当视线趋近于掠射角($\theta \to 90^\circ$)时,反射率会迅速上升,表面几乎变得像一面镜子。
7.4 金属与电介质的菲涅尔特性
菲涅尔公式不仅决定反射率随入射角变化,还直接影响物体的视觉颜色。根据材质的本质,可以分为金属(Metal)与电介质(Dielectric)两类:
金属(Metal)
由于大量自由电子的存在,对于金属界面,透射光进入材质内部会很快被吸收,不产生任何反射。
金属的颜色主要由其菲涅尔反射决定。由于菲涅尔反射率 $F_0$ 随波长变化明显,反射光带有金属本身的颜色。换句话说,对于金属而言,反照率(albedo)几乎等于 $F_0$,反射光就是我们看到的金属色。
因此,当光照射到金属表面时,只有部分光通过菲涅尔效应形成镜面反射,颜色由材质的 albedo(反照率)决定,而其余部分被吸收。
电介质(Dielectric)
对电介质,$F_0$ 由折射率(ior)决定,通常较低(例如 0.02–0.08),其公式为:
\[F_0 = \left( \frac{n - 1}{n + 1} \right)^2\]其中 $n$ 是材质的折射率。
这意味着电介质界面的反射光是白光,几乎不随波长变化。
入射光的大部分透射进入材质内部,对于不透明的电介质,这部分光会经过内部物质颗粒的反复散射吸收,颜色由材质的 albedo(反照率)决定,并以漫反射的形式反射回来。
因此,当光照射到电介质表面时,一部分光通过菲涅尔效应形成镜面反射(白光),而其余部分形成漫反射,其颜色由材质的 albedo(反照率)决定。
总结对比
| 材质类型 | F_0 特性 | 反射光颜色 | 漫反射 |
|---|---|---|---|
| 金属 | 随波长变化,可有色 | 有色(albedo) | 无 |
| 电介质 | 由折射率决定,通常较低 | 白光 | 有,颜色由 albedo 决定 |
通过这种方式,微平面分布 + 菲涅尔公式就完整解释了从入射光到观察到的反射高光和漫反射光的形成机制,这一过程中可控制的物质参数即为 PBR 材质中的 albedo/metallic/roughness/ior 参数。
7.5 金属和电介质 BSDF
我们结合前面介绍的 PBR 材质模型,以及微平面模型、菲涅尔公式,来看看 Taichi 如何实现金属和电介质材质的 BSDF。
MetalBSDF
class MetalBSDF:
@staticmethod
@ti.func
def cal_fresnel(dir, normal, albedo):
F0 = albedo
cos_theta = max(0.0, normal.dot(-dir))
return F0 + (1.0 - F0) * (1.0 - cos_theta) ** 5
@staticmethod
@ti.func
def sample(ray: ti.template(), hit: ti.template()):
n = _sample_normal(ray.rd, hit.normal, hit.material.roughness)
F = MetalBSDF.cal_fresnel(ray.rd, n, hit.material.albedo)
ray.l *= F
ray.ro = hit.point
ray.rd = _reflect(ray.rd, n)
-
cal_fresnel计算金属的反射系数:F0 = albedo:对于金属,固有反射率就是 albedo。cos_theta = normal.dot(-dir):入射光与法线夹角的余弦。- Schlick 近似公式:
F = F0 + (1-F0)*(1-cos_theta)**5。 - 结果
F控制反射光的强度。
-
sample方法描述光线的更新规则:_sample_normal根据粗糙度生成微平面法线n。- 计算菲涅尔反射系数
F。 ray.l *= F:反射光的能量乘以反射率。ray.ro = hit.point:更新光线起点到击中点。ray.rd = _reflect(ray.rd, n):沿镜面方向反射出去。
特点:金属 只产生反射光,不透射或漫反射。光线颜色由金属本身的
albedo决定。
DielectricBSDF
class DielectricBSDF:
@staticmethod
@ti.func
def cal_fresnel(dir, normal, ior):
F0 = ((ior - 1) / (ior + 1))**2
cos_theta = max(0.0, normal.dot(-dir))
return F0 + (1.0 - F0) * (1.0 - cos_theta) ** 5
@staticmethod
@ti.func
def sample(ray: ti.template(), hit: ti.template()):
n = _sample_normal(ray.rd, hit.normal, hit.material.roughness)
F = DielectricBSDF.cal_fresnel(ray.rd, n, hit.material.ior)
ray.ro = hit.point
if ti.random() > F:
ray.l *= hit.material.albedo
ray.rd = _sample_lambertian(hit.normal)
else:
ray.rd = _reflect(ray.rd, n)
-
cal_fresnel计算电介质界面的反射率:F0 = ((ior-1)/(ior+1))**2:由折射率决定。- Schlick 近似公式同样适用。
- 电介质表面反射的是白光,高光强度较低。
-
sample方法中:_sample_normal同样根据粗糙度生成微平面法线。- 计算菲涅尔反射系数
F。 ti.random() > F:用随机数决定光线是透射(漫反射)还是反射。- 如果透射(概率 1-F):颜色由 albedo 决定,沿着原始法线方向漫反射。
- 如果反射(概率 F):白光无衰减,沿微平面法向镜面方向反射。
特点:电介质 同时包含反射与漫反射。反射强度由折射率和入射光角度决定,漫反射颜色由 albedo 决定。
通过这两类 BSDF,我们的渲染器能够模拟现实中从镜面金属光泽到哑光陶瓷、塑料的各种材质行为。
7.6 运行示例
我们修改一下第六节的示例,给场景中的每个球都加上材质属性:
camera = Camera(resolution)
camera.set_direction(0, 0)
camera.set_position(Vec3f([0, 0, 4]))
# 中央球:蓝色哑光电介质
sphere1 = Sphere(Vec3f([0.0,0.0,0.0]), 0.5, material=Material(albedo=Vec3f([0.25, 0.25, 0.5]), roughness=0.5, metallic=0, ior=1.5))
# 左侧球:绿色光滑金属
sphere2 = Sphere(Vec3f([-1.0,0.0,0.0]), 0.5, material=Material(albedo=Vec3f([0.25, 0.5, 0.25]), roughness=0, metallic=1, ior=1.5))
# 右侧球:红色粗糙金属
sphere3 = Sphere(Vec3f([1.0,0.0,0.0]), 0.5, material=Material(albedo=Vec3f([0.5, 0.25, 0.25]), roughness=0.5, metallic=1, ior=1.5))
# 地面:灰色粗糙电介质
ground = Sphere(Vec3f([0,-10000.5,0.0]), 10000, material=Material(albedo=Vec3f([0.25, 0.25, 0.25]), roughness=0.5, metallic=0, ior=1.5))
world = World([sphere1, sphere2, sphere3, ground])
start_time = time.time()
render(world, camera)
print(f"Time elapsed: {time.time() - start_time:.2f}s")
ti.tools.imwrite(image, 'outputs/7_reflect.png')
结果如下图所示:

8. 光照:折射
代码:GitHub
在上一节中,我们通过微平面模型 + 菲涅尔公式实现了金属和电介质的镜面反射和漫反射效果。然而,许多电介质材质(如玻璃、水、宝石)不仅反射光,还允许光穿过材质——这就是折射(Refraction)现象。
首先,我们需要在 Material 结构体中增加 transparency 参数,表示材质是否透明:
Material = ti.types.struct(albedo=Vec3f, roughness=ti.f32, metallic=ti.i32, ior=ti.f32, transparency=ti.i32)
8.1 斯涅尔定律
折射是光从一种介质进入另一种介质时方向改变的结果,其规律由斯涅尔定律(Snell’s Law)描述:
\[n_1 \sin\theta_1 = n_2 \sin\theta_2\]其中:
- $n_1, n_2$ 分别为入射和透射介质的折射率;
- $\theta_1$ 为入射角(光线与法线夹角);
- $\theta_2$ 为折射角。
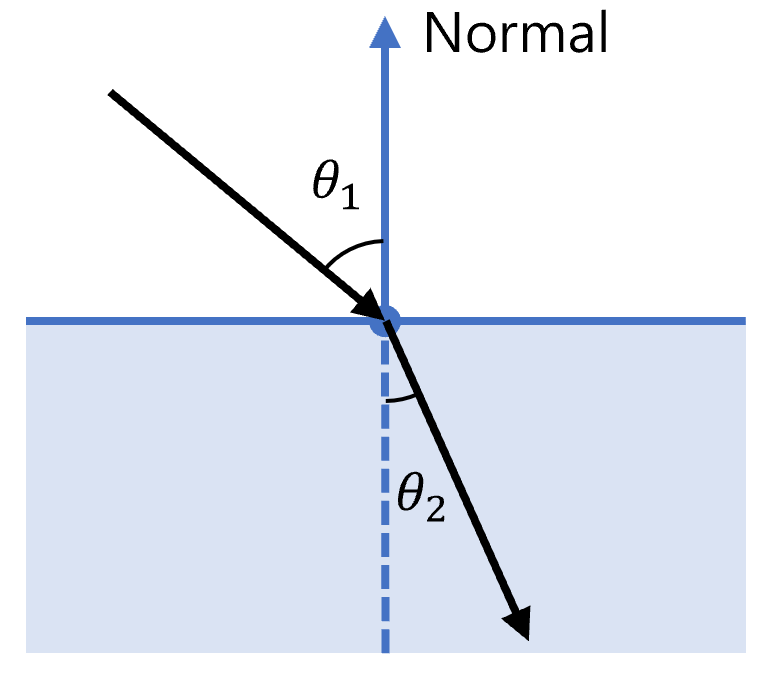
在代码中,折射光方向可以这么计算:
@ti.func
def _refract(dir, normal, ior):
k = dir.dot(normal)
r_out_perp = (dir - k * normal) / ior
r_out_perp_len2 = r_out_perp.dot(r_out_perp)
r = Vec3f(0)
if r_out_perp_len2 > 1:
r = _reflect(dir, normal)
else:
k = ti.sqrt(1.0 - r_out_perp_len2)
r_out_parallel = -k * normal
r = r_out_perp + r_out_parallel
return r
1. 公式分解
折射光可以分解为:
\[\mathbf{r} = \mathbf{r}_{\perp} + \mathbf{r}_{\parallel}\]其中:
- $\mathbf{r}_{\perp}$ 是折射方向在法线平面上的分量;
- $\mathbf{r}_{\parallel}$ 是沿法线的分量。
通过斯涅尔定律,入射光和折射光垂直于法线的分量之比即为介质的折射率,那么折射光的垂直分量可以计算为:
k = dir.dot(normal)
r_out_perp = (dir - k * normal) / ior
dir - k * normal 是入射方向在法线方向上的分量去掉后的投影,也就是 垂直于法线的分量。
2. 全反射判断
if r_out_perp_len2 > 1:
r = reflect(dir, normal)
如果垂直分量长度大于 1,意味着 $\sin \theta_2 > 1$,折射不成立,发生 全反射,方向退化为镜面反射。
3. 计算平行分量并组合
k = ti.sqrt(1.0 - r_out_perp_len2)
r_out_parallel = -k * normal
r = r_out_perp + r_out_parallel
k = sqrt(1 - sin²θ₂) = cos θ₂;r_out_parallel = -k * normal表示沿法线方向的折射分量;- 最终折射方向
r = r_out_perp + r_out_parallel。
8.2 电介质的完整 BSDF
补全上一节中实现的 DielectricBSDF 类,考虑折射,增加对透明度的支持
class DielectricBSDF:
@staticmethod
@ti.func
def cal_fresnel(dir, normal, ior):
F0 = ((ior - 1) / (ior + 1))**2
cos_theta = max(0.0, normal.dot(-dir))
return F0 + (1.0 - F0) * (1.0 - cos_theta) ** 5
@staticmethod
@ti.func
def sample(ray: ti.template(), hit: ti.template()):
n = _sample_normal(ray.rd, hit.normal, hit.material.roughness)
F = DielectricBSDF.cal_fresnel(ray.rd, n, hit.material.ior)
ray.ro = hit.point
if ti.random() > F:
ray.l *= hit.material.albedo
if hit.material.transparency:
ray.rd = _refract(ray.rd, n, hit.material.ior)
else:
ray.rd = _sample_lambertian(hit.normal)
else:
ray.rd = _reflect(ray.rd, n)
其余部分的实现,包括微平面法线的生成、菲涅尔反射系数的计算与之前一致。不同之处在于:
若材质透明,则透射部分光线以斯涅尔定律计算折射方向,区别于不透明材质的漫反射
这样,我们就可以同时实现考虑表面粗糙度情况下电介质的反射、折射和漫反射,自然地呈现磨砂玻璃、水等透明材质的视觉效果。
8.3 补全求交逻辑
因为现在光线有可能会进入物体内部,我们需要对求交逻辑进行调整,以保证法线方向始终指向入射方向,并在折射计算中正确处理折射率比。具体来说:
- 翻转法线:当光线从球体内部射出时,入射方向与表面法线同向,需要将法线取反,使其指向外部;
- 调整折射率:同时将折射率取倒数 $1 / \text{ior}$,对应光线从高折射率介质进入低折射率介质的情况;
- 选择正确的交点:在二次求交中,如果最近交点非常靠近光线起点(例如光线在球体内部),且材质允许透射,则选择远的交点,从而保证光线能够穿过物体内部,实现折射效果。
通过这些补充逻辑,我们可以在路径追踪中自然地处理光线进入和离开透明物体的场景,使折射计算和菲涅尔反射正确匹配,从而生成逼真的透明材质效果。
@ti.data_oriented
class World:
@ti.func
def hit(self, ray):
res = HitRecord(0.0)
res.t = -1
for i in range(self.size):
record = self.spheres[i].hit(ray)
if record.t >= 1e-4 and (res.t < 0 or record.t < res.t): res = record
+ if ray.rd.dot(res.normal) > 0:
+ res.normal = -res.normal
+ res.material.ior = 1 / res.material.ior
return res
这里处理了光线进入物体内部的情况:
如果光线方向和表面法线方向同向(dot > 0),说明光线从内部射出。此时需要翻转法线,确保折射计算中的法线始终指向外部,同时折射率取倒数 1 / ior,对应光线从高折射率介质进入低折射率介质。
@ti.dataclass
class Sphere:
center: Vec3f
radius: ti.f32
material: Material
@ti.func
def hit(self, ray):
oc = ray.ro - self.center
a = 1
b = 2.0 * ti.math.dot(oc, ray.rd)
c = ti.math.dot(oc, oc) - self.radius**2
discriminant = b**2 - 4 * a * c
record = HitRecord(0.0)
record.t = -1
if discriminant >= 0:
+ sqrt_discriminant = ti.sqrt(discriminant)
+ record.t = (-b - sqrt_discriminant) / (2.0 * a)
+ if record.t < 1e-4 and self.material.transparency:
+ record.t = (-b + sqrt_discriminant) / (2.0 * a)
record.point = ray.ro + record.t * ray.rd
record.normal = (record.point - self.center).normalized()
record.material = self.material
return record
一般二次求交公式有两个解:
\[t = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]-b - sqrt_discriminant对应最近的交点(前表面);-b + sqrt_discriminant对应远的交点(后表面)。
当最近交点在 t < 1e-4(非常近或光线在内部)且材质可透明(transparency)时,才选择远的交点,这样光线可以穿过物体内部实现折射。这样处理可以解决光线从内部出射的场景。
8.4 渲染示例
camera = Camera(resolution)
camera.set_direction(0, 0)
camera.set_position(Vec3f([0, 0.4, 4]))
# 下层中央球:蓝色哑光电介质
sphere1 = Sphere(Vec3f([0.0,0.0,0.0]), 0.5, material=Material(albedo=Vec3f([0.25, 0.25, 0.5]), roughness=0.5, metallic=0, ior=1.5))
# 下层左侧球:绿色光滑金属
sphere2 = Sphere(Vec3f([-1.0,0.0,0.0]), 0.5, material=Material(albedo=Vec3f([0.25, 0.5, 0.25]), roughness=0, metallic=1, ior=1.5))
# 下层右侧球:红色粗糙金属
sphere3 = Sphere(Vec3f([1.0,0.0,0.0]), 0.5, material=Material(albedo=Vec3f([0.5, 0.25, 0.25]), roughness=0.5, metallic=1, ior=1.5))
# 上层左侧球:无色光滑透明电介质
sphere4 = Sphere(Vec3f([-0.5,0.866,0]), 0.5, material=Material(albedo=Vec3f([1, 1, 1]), roughness=0, metallic=0, ior=1.5, transparency=1))
# 上层右侧球:绿色粗糙透明电介质
sphere5 = Sphere(Vec3f([0.5,0.866,0]), 0.5, material=Material(albedo=Vec3f([0.5, 1, 0.5]), roughness=0.5, metallic=0, ior=1.5, transparency=1))
# 地面:灰色粗糙电介质
ground = Sphere(Vec3f([0,-10000.5,0.0]), 10000, material=Material(albedo=Vec3f([0.25, 0.25, 0.25]), roughness=0.5, metallic=0, ior=1.5))
world = World([sphere1, sphere2, sphere3, sphere4, sphere5, ground])
start_time = time.time()
render(world, camera)
print(f"Time elapsed: {time.time() - start_time:.2f}s")
ti.tools.imwrite(image, 'outputs/8_refract.png')
渲染效果如下:

9. 景深模糊
代码:GitHub
在前面的章节中,我们的相机模型都是针孔相机(pinhole camera):每条光线都从同一点出发,穿过像素方格采样场景。这种模型虽然简洁,但生成的图像总是所有景物都完全清晰,缺少真实相机的景深效果。
现实相机和人眼都有景深现象:焦距附近的物体清晰,而前景或背景会模糊,这称之为景深模糊(Depth of Field, DoF)。
实现景深效果,需要对光线生成进行扩展,引入光圈(aperture)和焦平面(focal plane)的概念。
9.1 景深原理
真实相机的成像过程由镜头系统决定。理想的针孔相机由于光圈无限小,可以保证任意远近的光线都严格通过针孔并在成像平面上汇聚,因此不会产生景深模糊。然而在现实中,镜头必须具有一定大小的光圈,以便让足够的光线进入,这也正是景深现象产生的根源。
当物体位于与镜头焦距匹配的位置时,来自该点的所有光线会在成像平面上准确汇聚,形成清晰的成像;这时的成像平面被称为焦平面。如果物体不在焦平面上,穿过光圈的光线将无法在成像平面上收敛为单一点,而是扩散成一个小圆斑。小圆斑越大,画面中的该物体就越模糊。只有当物体处于某一深度范围内时,其弥散斑才会小到足以被认为是清晰的,这个范围便被称为景深。
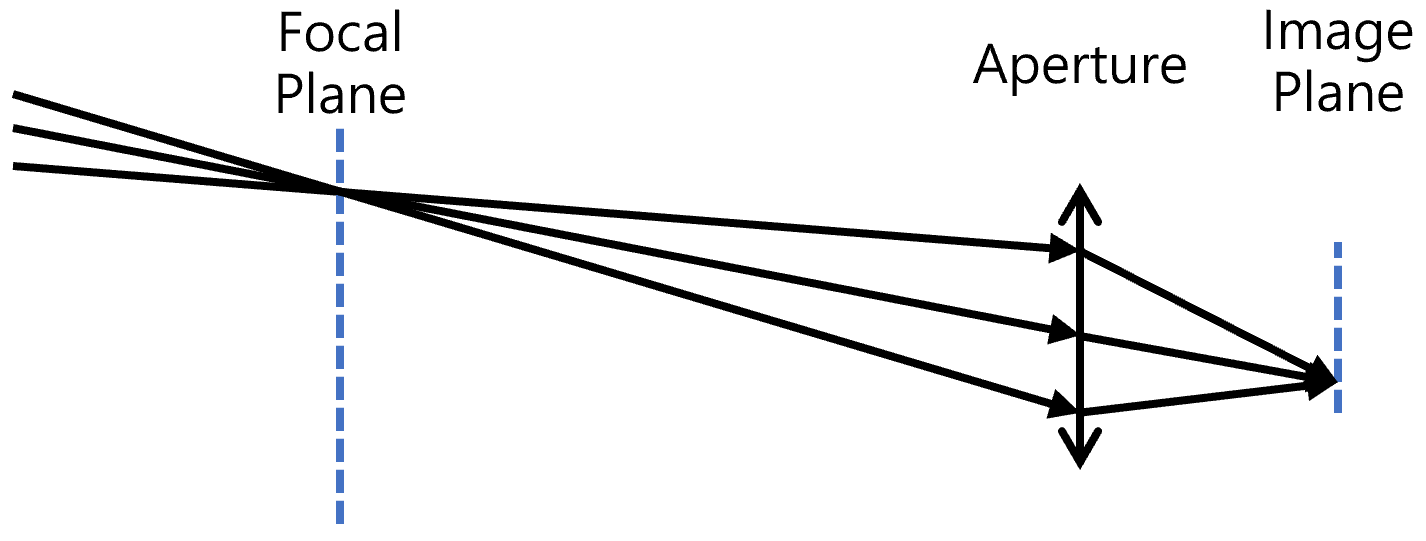
从路径追踪的角度看,景深的模拟方式十分直观。我们希望追踪的是最终在成像平面上落入某个像素的光线。但与针孔模型不同,这些光线的起点并非唯一,而是分布在整个光圈圆盘上;在经过镜头折射前,它们都会穿过焦平面上的对应点。通过在光圈圆盘上随机采样多个出射点,并将这些光线统一穿过到焦平面上的对应像素方格,就可以自然重现景深模糊的效果。光圈越大,离焦物体的弥散斑越大,模糊感越强烈;光圈越小,景深范围就越宽广,成像效果也越接近针孔相机的“全清晰”状态。
9.2 相机模型扩展
在相机模型中,我们需要增加两个参数:
focal_length:焦距,即相机与焦平面的距离;aperture:光圈大小,即相机镜头系统的透光范围的直径。
@ti.data_oriented
class Camera:
def __init__(self, resolution, fov=60, focal_length=1, aperture=0):
self.resolution = resolution
self.fov = float(fov)
+ self.focal_length = float(focal_length)
+ self.aperture = float(aperture)
self.position = Vec3f(0)
self.yaw = 0.0
self.pitch = 0.0
self.roll = 0.0
9.3 光线生成
在引入光圈后,光线不再总是从相机中心出发,而是从光圈圆盘上的不同位置随机采样。为了实现这一点,我们需要一个辅助函数,用于在单位圆盘内均匀采样随机点:
@ti.func
def sample_in_disk():
r = ti.sqrt(ti.random(ti.f32)) # 半径开方,保证均匀分布
theta = 2 * ti.math.pi * ti.random(ti.f32) # 随机角度
x = r * ti.cos(theta)
y = r * ti.sin(theta)
return Vec2f([x, y])
其中对半径 $r$ 需要开方,证明如下:
设采样点为 $\boldsymbol p$,则 $r$ 的累积分布函数(CDF)为
\[\mathrm{CDF}(r) = P(\|\boldsymbol p\| \leq r) = \frac{\pi r^2}{\pi} = r^2\]因此,为了实现最终的均匀采样,对 $r$ 的采样需要按照其累积分布函数的反函数进行,即
\[r = \sqrt{\epsilon} \quad \epsilon \sim U(0, 1)\]这个函数返回一个落在单位圆内的二维向量 (x, y),用来表示光圈圆盘上的采样位置。
随后我们只需将这个结果缩放到实际光圈大小,就能得到光线的随机出射点。
在针孔相机模型中,每条光线的起点都是相机位置,方向由像素在视平面上的位置决定。而在引入景深后,光线的生成过程需要额外考虑光圈和焦平面:
@ti.data_oriented
class Camera:
@ti.kernel
def get_rays(self, rays: ti.template()):
width = self.resolution[0]
height = self.resolution[1]
x = self.position[0]
y = self.position[1]
z = self.position[2]
trans = rotate(self.yaw, self.pitch, self.roll)
ratio = height / width
view_width = 2 * ti.tan(ti.math.radians(self.fov) / 2)
view_height = view_width * ratio
direction = trans @ Vec3f([0.0, 0.0, -1.0])
width_axis = trans @ Vec3f([1.0, 0.0, 0.0])
height_axis = trans @ Vec3f([0.0, 1.0, 0.0])
for i, j in rays:
# 焦平面上的目标点
target = self.focal_length * (
direction
+ ((i + ti.random(ti.f32)) / width - 0.5) * view_width * width_axis
+ ((j + ti.random(ti.f32)) / height - 0.5) * view_height * height_axis
)
# 光圈圆盘上的随机采样
sample = sample_in_disk()
origin = self.aperture / 2.0 * (
sample[0] * width_axis + sample[1] * height_axis
)
# 构造射线
rays[i, j].ro = self.position + origin
rays[i, j].rd = (target - origin).normalized()
rays[i, j].l = Vec3f([1.0, 1.0, 1.0])
- 首先确定像素对应的焦平面目标点。这相当于针孔模型中原本的射线方向,但这里我们将射线延伸到与相机保持
focal_length距离的平面上,得到该像素的聚焦点。 - 然后在光圈圆盘上随机采样一个点,作为射线的实际出发位置。这一步模拟了光圈有限大小的特性。
- 最后,让射线从采样点出发,指向对应的焦平面目标点。这样生成的射线便能自然表现出景深模糊效果。
这样,景深模糊的实现就完整了。通过调整 focal_length 可以改变清晰的对焦平面;通过调整 aperture 可以控制景深范围的大小。
9.4 渲染示例
示例使用的场景与上一节相同,我们调整相机的视角以更好的体现景深模糊效果:
camera = Camera(resolution)
camera.set_position(Vec3f([3, 0.5, 2]))
camera.look_at(Vec3f([0.0,0.35,0.0]))
camera.set_len(focal_length=camera.position.norm(), aperture=0.2)
渲染效果如下:

10. 最终效果
代码:GitHub
在本文的最后,我们构建一个包含数百个随机材质小球的场景。为了让效果更丰富,他们将随机被赋予漫反射、金属和玻璃等材质。
场景中会额外放置几个较大的特殊球体作为视觉重点,展示出不同材质的渲染效果。
def random_scene(size=11):
world = World()
ground = Sphere(Vec3f([0,-10000,0]), 10000, material=Material(albedo=Vec3f([0.25, 0.25, 0.25]), roughness=0.5, metallic=0, ior=1.5, transparency=0))
world.add(ground)
for a in range(-size, size):
for b in range(-size, size):
choose_mat = random.random()
center = Vec3f([a + 0.9 * random.random(), 0.2, b + 0.9 * random.random()])
if (center - Vec3f([4, 0.2, 0])).norm() > 0.9:
albedo = Vec3f([random.random(), random.random(), random.random()])
if choose_mat < 0.8:
# diffuse
sphere = Sphere(center, 0.2, material=Material(albedo=albedo, roughness=random.random(), metallic=0, ior=1.5, transparency=0))
world.add(sphere)
elif choose_mat < 0.95:
# metal
sphere = Sphere(center, 0.2, material=Material(albedo=0.5+0.5*albedo, roughness=0.5*random.random(), metallic=1, ior=0, transparency=0))
world.add(sphere)
else:
# glass
sphere = Sphere(center, 0.2, material=Material(albedo=0.75+0.25*albedo, roughness=0.2*random.random(), metallic=0, ior=1.5, transparency=1))
world.add(sphere)
sphere = Sphere(Vec3f([0, 1, 0]), 1.0, material=Material(albedo=Vec3f([1, 1, 1]), roughness=0, metallic=0, ior=1.5, transparency=1))
world.add(sphere)
sphere = Sphere(Vec3f([-4, 1, 0]), 1.0, material=Material(albedo=Vec3f([0.4, 0.2, 0.1]), roughness=0.5, metallic=0, ior=1.5, transparency=0))
world.add(sphere)
sphere = Sphere(Vec3f([4, 1, 0]), 1.0, material=Material(albedo=Vec3f([0.7, 0.6, 0.5]), roughness=0, metallic=1, ior=0, transparency=0))
world.add(sphere)
return world
运行渲染代码,在几分钟的等待后,我们得到如下结果:

至此,我们的路径追踪器已经支持了多种基础材质:包括表现粗糙漫反射的电介质、具有强烈高光的金属,以及折射透明的玻璃。我们用基于物理的视角,将这些材质的性质与光线追踪的原理相结合,实现了渲染出更加真实、更具表现力的图像。
在相机建模方面,我们也超越了单一的针孔模型。允许调节焦距和光圈大小,从而更灵活地控制成像效果,使我们的渲染结果更加接近真实摄影。例如,当光圈开启时,非焦点区域会自然出现虚化模糊,这种模糊并非后期滤镜,而是路径追踪过程中由光学原理直接产生的结果。
欢呼吧!🎉🎉🎉
下一步
到目前为止,我们已经完成了一个基础路径追踪器:它可以渲染包含漫反射、金属和玻璃材质的球体场景,并支持可调节焦距与光圈的景深效果。然而,在处理大规模场景时仍存在性能瓶颈。例如,在最终示例中,渲染数百个球体时,由于采用暴力求交,单帧图像仍需要几分钟才能生成,这在实际应用中显然不够高效。
为了解决这一问题,下一阶段将引入空间加速结构(Acceleration Structures),最典型的例子是包围体层次结构(BVH, Bounding Volume Hierarchy)。通过将场景中的几何体组织成层次化的包围盒,光线可以快速排除大部分不相交的物体,从而显著减少求交次数,提高渲染效率。
同时,为了支持更丰富的场景表现,我们计划扩展渲染器以支持任意三角形网格(Mesh)和材质贴图。这不仅使渲染器能够处理复杂模型,如建筑、角色或道具,也让大量三角形能够充分利用 BVH 加速,即使在大型场景中也能保持较高的渲染性能。
结合以上两个方向,下一篇内容将以“Mesh 与空间加速结构”为主题。这部分代码是笔者很久之前写的,整理其中的逻辑亦需要一些时间,不过相信几周之内就能和大家见面。
