前言

图片缩放是我实现添加文字的基础，也是图像处理中最基础的操作之一，但是这最基础的操作中，也隐含着对信息的思考，刚刚学习的信号与系统也能发挥作用。

透明度支持

图片缩放一般同时伴随着图片插入，我的添加文字的方法本质也是将缩小后的文字图片插入原图中。但是谁也不希望自己插入的图片、文字在原图中留下突兀的纯色背景，所以添加 Image 类对于透明色的支持很重要

在 Color 类中新增 Color overlie(Color, Color) 方法，实现两个含透明度颜色的叠加。

透明色的叠加可以理解为光通过时的反射与透射叠加的效果，透明度为光的反射率。假设有强度 1 的光线入射这个像素，作为上层颜色$C_1$（设其透明度$k_1$），有强度 $k_1$ 的光线会被反射，形成 $k_1\times C_1$ 的反射光。同时强度 $1-k_1$ 的光线透射到下层颜色$C_2$上（设其透明度$k_2$），则透射光的 $k_2$，强度为 $(1-k_1)\times k_2$ 的光被反射，形成 $(1-k_1)\times k_2\times C_2$ 的反射光。剩余的部分为强度 $(1-k_1)\times (1-k_2)$。则总的透明度即为 1 减去此，总的颜色为两个反射光相加再除以总透明度，算法为：

static Color Color::overlie(Color C1, Color C2)
{
    Color res;
    double alpha = 1 - (1 - C1.alpha) * (1 - C2.alpha);
    res.rgba((C1.alpha * C1.red + (1 - C1.alpha) * C2.alpha * C2.red) / alpha,
            (C1.alpha * C1.green + (1 - C1.alpha) * C2.alpha * C2.green) / alpha,
            (C1.alpha * C1.blue + (1 - C1.alpha) * C2.alpha * C2.blue) / alpha,
            alpha);
    return res;
}

修改原 Image 类，加入透明度支持。而且由于图片缩放会产生新的Image对象，有对象返回与拷贝的需求，所以要完善拷贝与转移等构造、赋值函数以及文件读取函数。

class Image
{
    private:
        //数据在内存中保存为一个像素点对应一个Color对象，24位彩色加上浮点数alpha通道，不再直接为文件数据区的映像
        Color* data;
        uint32_t width;
        uint32_t height;

    public:
        //新增|默认构造函数
        Image()
        {
            this->width = 0;
            this->height = 0;
            data = NULL;
        }

        //修改|构造函数
        Image(uint32_t width, uint32_t height)
        {
            this->width = width;
            this->height = height;
            //更改data的初始化，初始化为全透明背景
            data = new Color[width * height];
            for (int i = 0; i < width * height; i++)
                data[i].rgba(0, 0, 0, 0);
        }

        //新增|拷贝构造函数
        Image(Image& I)
        {
            width = I.width;
            height = I.height;
            data = new Color[width * height];
            for (int i = 0; i < width * height; i++)
                data[i] = I.data[i];
        }

        //新增|转移构造函数
        Image(Image&& I)
        {
            width = I.width;
            height = I.height;
            data = I.data;
            I.data = NULL;
        }

        //新增|拷贝赋值函数
        Image& operator=(Image& I)
        {
            delete[] data;
            width = I.width;
            height = I.height;
            data = new Color[width * height];
            for (int i = 0; i < width * height; i++)
                data[i] = I.data[i];
            return *this;
        }

        //新增|转移赋值函数
        Image& operator=(Image&& I)
        {
            delete[] data;
            width = I.width;
            height = I.height;
            data = I.data;
            I.data = NULL;
            return *this;
        }

        //新增|按透明度叠加像素
        void overliePixel(uint32_t x, uint32_t y, Color color)
        {
            setPixel(x, y, Color::overlay(color, getPixel(x, y)));
        }

        //修改|绘制基本图形
        Image& draw(Figure& s)
        {
            Figure::AABBdata b = s.tAABB();
            int xMin = max((int)floor(b.xMin), 0);
            int yMin = max((int)floor(b.yMin), 0);
            int xMax = min((int)ceil(b.xMax), (int)width - 1);
            int yMax = min((int)ceil(b.yMax), (int)height - 1);
            for (int u = xMin; u <= xMax; u++)
                for (int v = yMin; v <= yMax; v++)
                {
                    double SDF = s.tSDF({u, v});
                    if (SDF < 0)
                    //更改设置颜色为叠加颜色
                    overliePixel(u, v, s.getAttribute().color);
                }
            return *this;
        }

        //新增|BMP文件头结构体
        #pragma pack(2)     //按2字节对齐，避免结构体中空位
        typedef struct
        {
            uint16_t bfType;
            uint32_t bfSize;
            uint16_t bfReserved1;
            uint16_t bfReserved2;
            uint32_t bfOffBits;
            uint32_t biSize;
            uint32_t biWidth;
            uint32_t biHeight;
            uint16_t biPlanes;
            uint16_t biBitCount;
            uint32_t biCompression;
            uint32_t biSizeImage;
            uint32_t biXPelsPerMeter;
            uint32_t biYPelsPerMeter;
            uint32_t biClrUsed;
            uint32_t biClrImportant;
        }BMPHead;
        #pragma pack()      //取消自定义对齐设置

        //新增|读取BMP文件
        Image& readBMP(const char* filename)
        {
            delete[] data;
            fstream file(filename, ios::in | ios::binary);
            BMPHead head;
            file.read((char*)&head, 54);

            //暂时支持24位深度不压缩
            if (head.biBitCount != 24 || head.biCompression != 0)
            {
                cout<<"Error: unsupported file.\n";
                exit(0);
            }

            //按文件头部的信息创建空间
            this->width = head.biWidth;
            this->height = head.biHeight;
            data = new Color[width * height];

            //读取数据
            int fillNum = (4 - (3 * width) % 4) % 4;
            for (int i = 0; i < height; i++)
            {
                for (int j = 0; j < width; j++)
                {
                    file.read((char *)&data[i * width + j].blue, 1);
                    file.read((char *)&data[i * width + j].green, 1);
                    file.read((char *)&data[i * width + j].red, 1);
                    data[i * width + j].alpha = 1;
                }
                file.seekg(fillNum, ios::cur);
            }
            file.close();
            return *this;
        }

        //修改|保存BMP文件
        void saveBMP(const char* filename)
        {
            //构造文件头
            uint32_t size = width*height*3+54;
            BMPHead head={
                0x4D42,             //bfType("BM")
                size,               //bfSize
                0x0000,0x0000,      //bfReserved1,2(0)
                0x00000036,         //bfOffBits(54)
                0x00000028,         //biSize(40)
                width,              //biWidth
                height,             //biHeight
                0x0001,             //biPlanes(1)
                0x0018,             //biBitCount(24)
                0x00000000,         //biCompression(0, 无压缩)
                0x00000000,         //biSizeImage(缺省)
                0x00000000,         //biXPelsPerMeter(缺省)
                0x00000000,         //biYPelsPerMeter(缺省)
                0x00000000,         //biClrUsed(0,全部颜色)
                0x00000000          //biClrImportant(0,全部颜色)
            };

            //打开文件
            cout<<"Exporting...\n";
            fstream file(filename, ios::out | ios::binary);
            if (!file)
            {
                cout<<"Error: File open failed.\n";
                return;
            }

            //写入文件头
            file.write((char*)&head,54);

            //写入数据
            uint8_t fillBytes[3] = {0};
            int fillNum = (4 - (3 * width) % 4) % 4;
            Color final;
            for (int i = 0; i < height; i++)
            {
                for (int j = 0; j < width; j++)
                {
                    final = Color::overlie(data[i * width + j], {255, 255, 255});
                    file.write((char *)&final.blue, 1);
                    file.write((char *)&final.green, 1);
                    file.write((char *)&final.red, 1);
                }
                file.write((char *)fillBytes, fillNum);
            }
            file.close();
        }
}

画三个半透明圆尝试一下：

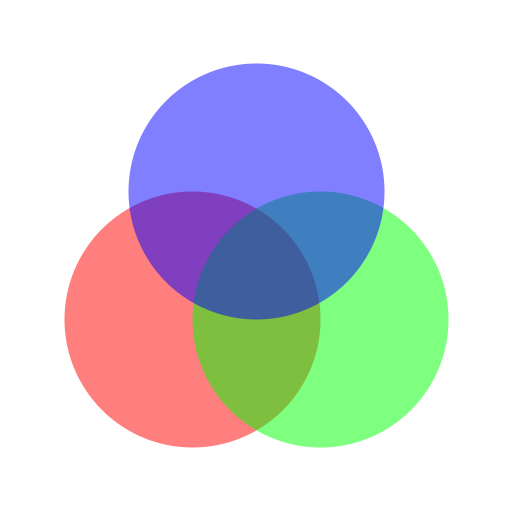
效果正确！

重采样与卷积

先看一下重采样的定义：

重采样是指，对一个已知的离散采样信号，通过计算，改变其采样率，得到新的信号的过程。若采样率提升，则称为上采样，否则称为下采样。

采样是一个信号与系统中的经典的模型，一个连续信号时域上的采样对应原信号频域上的周期叠加。

设原信号 $x(t)$，采样频率 $\omega_s$，采样结果为 $x_s[n]$

\[\begin{gather} x_s[n]=x(\frac{2\pi n}{\omega_s})\\ x_s(t)=\sum_{n=-\infty}^{+\infty}x_s[n]\delta(t-\frac{2\pi n}{\omega_s})=x(t)\cdot\sum_{n=-\infty}^{+\infty}\delta(t-\frac{2\pi n}{\omega_s})\\ X_s(j\omega)=\frac1{2\pi}X(j\omega)*\mathcal F\left(\sum_{n=-\infty}^{+\infty}\delta(t-\frac{2\pi n}{\omega_s})\right) \end{gather}\]

因为右边一项是周期信号，可求傅里叶级数

\[D_n=\frac{\omega_s}{2\pi}\int_{-\frac\pi{\omega_s}}^{\frac\pi{\omega_s}}\delta(t)e^{-jn\omega_st}\mathrm dt=\frac{\omega_s}{2\pi}\]

所以

\[\begin{gather} \sum_{n=-\infty}^{+\infty}\delta(t-\frac{2\pi n}{\omega_s})=\sum_{n=-\infty}^{+\infty}D_ne^{jn\omega_st}=\frac{\omega_s}{2\pi}\sum_{n=-\infty}^{+\infty}e^{jn\omega_st}\\ \mathcal F\left(\sum_{n=-\infty}^{+\infty}\delta(t-\frac{2\pi n}{\omega_s})\right)=\frac{\omega_s}{2\pi}\sum_{n=-\infty}^{+\infty}2\pi\delta(\omega-n\omega_s)=\omega_s\sum_{n=-\infty}^{+\infty}\delta(\omega-n\omega_s) \end{gather}\]

最终可求得采样信号的傅里叶变换为

\[X_s(j\omega)=\frac1{2\pi}X(j\omega)*\omega_s\sum_{n=-\infty}^{+\infty}\delta(t-n\omega_s)=\frac{\omega_s}{2\pi}\sum_{n=-\infty}^{+\infty}X(\omega-n\omega_s)\]

可见采样信号的傅里叶变换对应原信号的傅里叶变换的周期叠加。

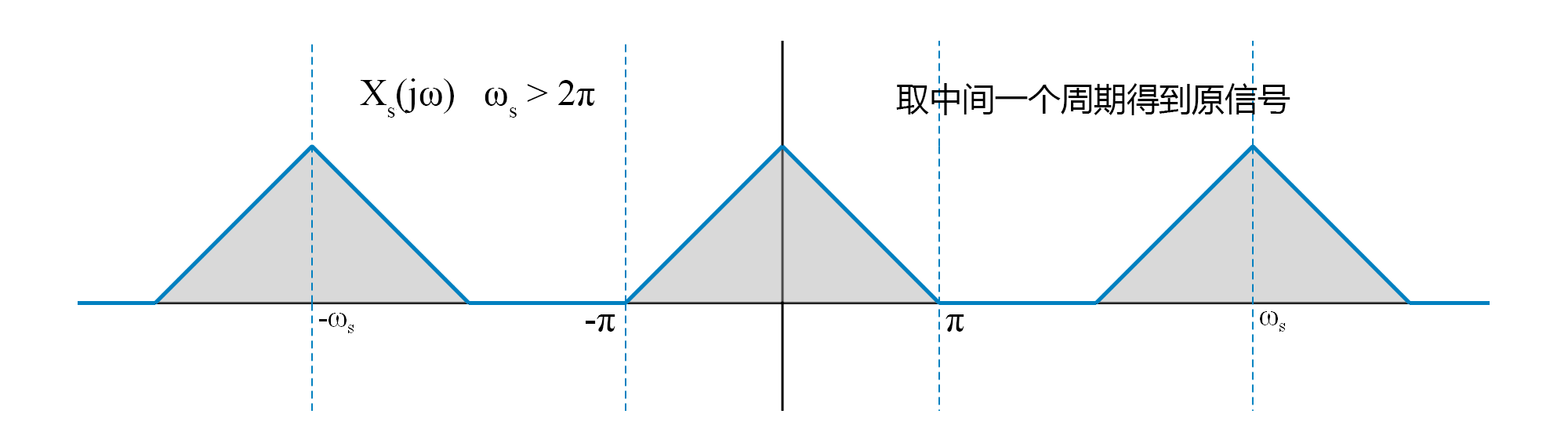
那么问题来了，现在我们已知采样信号，能还原出原信号吗？根据采样信号的傅里叶变换形式，我们发现他是周期为 $\omega_s$ 的函数，若原信号的傅里叶变换在 $\lvert\omega\rvert>\frac{\omega_s}{2}$ 的时候为 $0$，则可以完全恢复原信号，这就是奈奎斯特采样定律。

那么我们就不妨假设

\[X(j\omega)=\frac{2\pi}{\omega_s}X_s(j\omega)G_{\omega_s}(\omega)\quad G_k(\omega)=\left\{\begin{split}&1\quad&|\omega|<\frac k2\\&\frac12\quad&|\omega|=\frac k2\\&0\quad&|\omega|>\frac k2\end{split}\right.\]

则

\[x(t)=\mathcal F^{-1}(X(j\omega))=\frac{2\pi}{\omega_s}\mathcal F^{-1}(X_s(j\omega)G_{\omega_s}(\omega))=\frac{2\pi}{\omega_s}\sum_{n=-\infty}^{+\infty}x_s[n]\delta(t-\frac{2\pi n}{\omega_s})*\frac{\sin\frac{\omega_s}2t}{\pi t}\]

一般而言，我们在重建连续信号时会使 $x(n)=x[n]$，采样率即为 $\omega_s=2\pi$，代入得

\[x(t)=\sum_{n=-\infty}^{+\infty}x[n]\delta(t-n)*\frac{\sin\pi t}{\pi t}=\sum_{n=-\infty}^{+\infty}x[n]\delta(t-n)*\mathrm{sinc}\ t=\sum_{n=-\infty}^{+\infty}x[n]\mathrm{sinc}(t-n)\]

这样一来我们就重建得到了连续信号

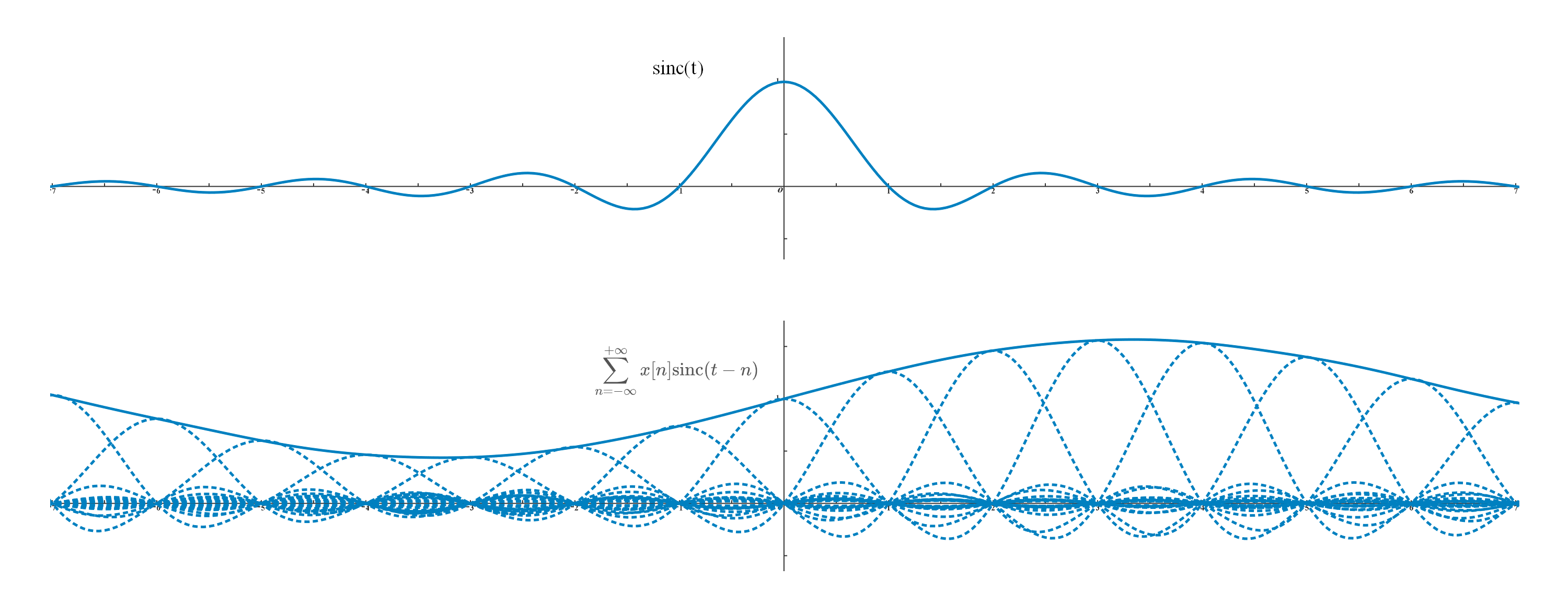
从公式中我们可以看出，从采样信号重建连续信号，对应的操作为采样信号卷积一个特定的函数，称为卷积核，这里为 $\mathrm{sinc}\ t$ 函数。

上采样

上采样指提高采样频率，增加数据点，也称作内插、插值。由于提高的采样频率肯定满足奈奎斯特采样定律，频域不会发生混叠，所以直接按对应的时间在重建的连续信号（卷积 $\mathrm{sinc}\ t$）中采样即可。

下采样

下采样指降低采样频率，减少数据点。减少的采样率会导致频域的混叠，会丢失一部分频谱：

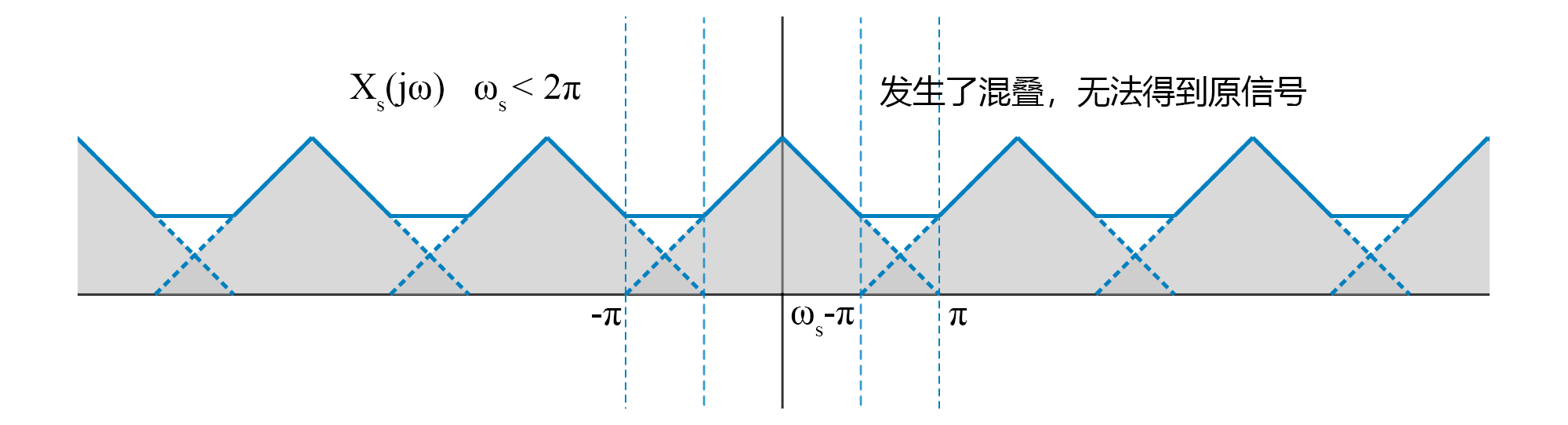
观察上图中混叠的频谱，可以发现只有低频部分保持了与原始信号频谱的一致性，而相当多的高频由于混叠而失去了原始频谱，未失真的频谱宽度只有 $\omega_s-\pi$。频谱丢失得越多说明信号的失真越大，因此为了减少失真，需要尽可能保留更多的原始信号频谱，也就是说，我们要尽可能减少混叠。

怎么做呢？这时就要用到抗混叠滤波器（anti-aliasing filter），就是一个截止频率为 $\frac{\omega_s}{2}$ 的理想低通滤波器。原信号通过这样一个滤波器后，去除高频分量，保留低频分量，使原信号的频谱最高非零频率为 $\frac{\omega_s}2$，满足奈奎斯特采样定律从而在采样后避免混叠。

\[\begin{gather} X'(j\omega)=X(j\omega)G_{\omega_s}(\omega)=X_s(j\omega)G_{2\pi}(\omega)G_{\omega_s}(\omega)=X_s(j\omega)G_{\omega_s}(\omega)\\ x'(t)=\sum_{n=-\infty}^{+\infty}x[n]\delta(t-n)*\frac{\sin\frac{\omega_s}2t}{\pi t}=\sum_{n=-\infty}^{+\infty}x[n]\delta(t-n)*\frac{\omega_s}{2\pi}\mathrm{sinc}(\frac{\omega_s}{2\pi}t)=\sum_{n=-\infty}^{+\infty}x[n]\frac{\omega_s}{2\pi}\mathrm{sinc}(\frac{\omega_s}{2\pi}t) \end{gather}\]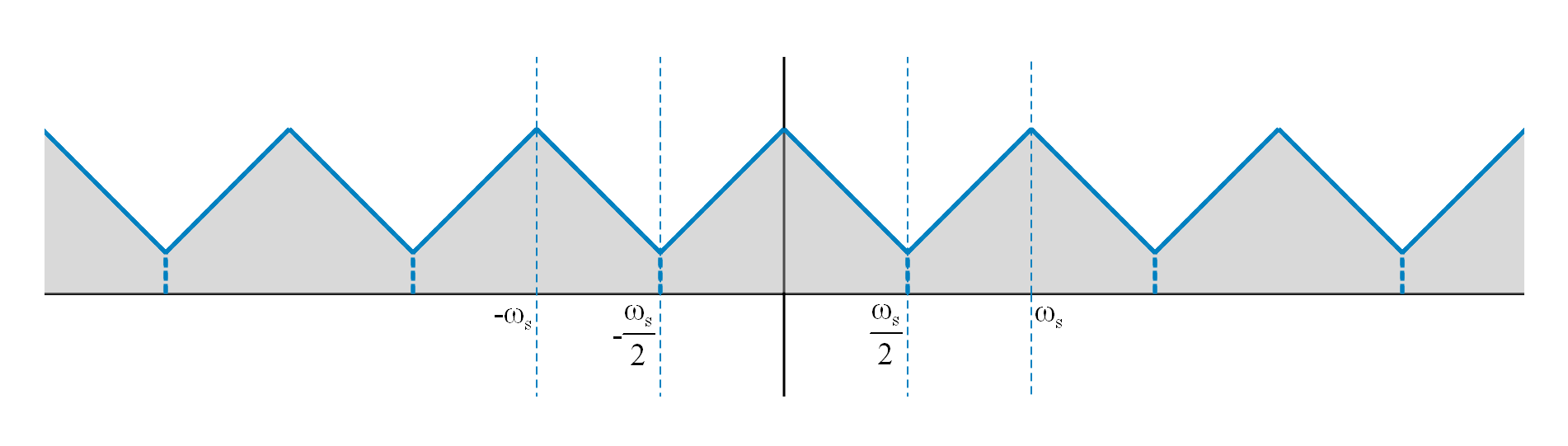

这样一来保留了宽度 $\frac{\omega_s}{2}$ 的未失真频谱，明显优于未处理的情况。下采样信号即为对原采样信号卷积 $\frac{\omega_s}{2\pi}\mathrm{sinc}(\frac{\omega_s}{2\pi}t)$ 后的的重建连续信号按对应时间采样。

更多卷积核

上面分析的是理论上最完备的重采样的方法，可见其时域和频域：

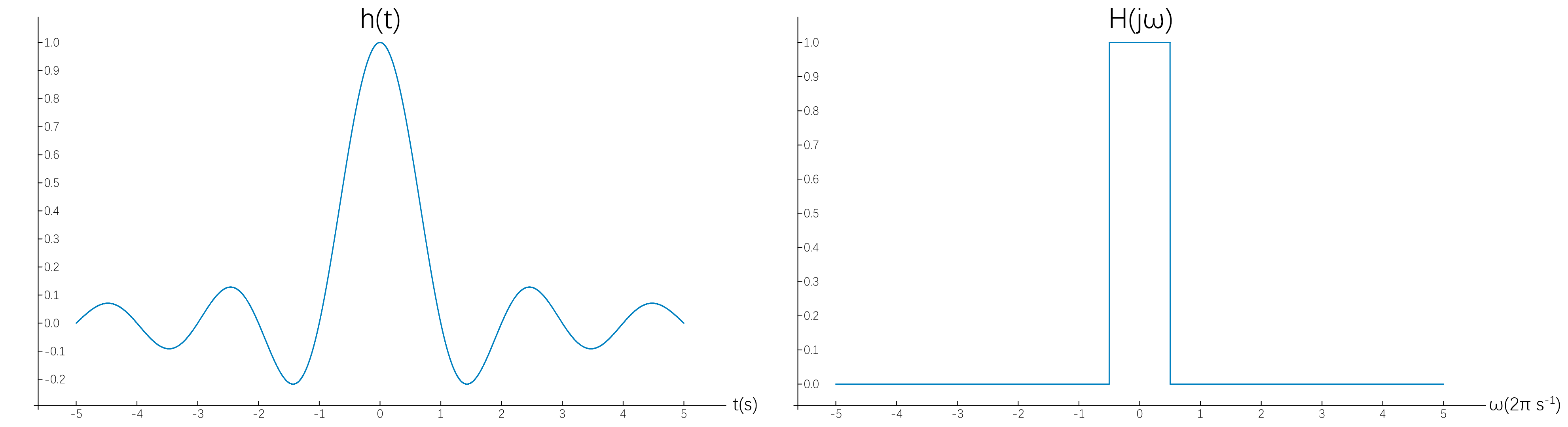
但是 sinc 函数的属性使得每一点的插值与全部数据相关，这对于边界拓展和计算的时间复杂度是非常致命的。即，为了在边界处达到良好的插值效果，必须将信号拓展很长一段，并且复杂度几乎达到 O(n^2)。所以，构造一些有限关联的卷积核非常重要。

这些卷积核有几个必要条件：

  • 为偶函数，这是基本对称性的要求
  • 有限非0值区间，即 $h(t)=0 (\lvert t\rvert>T)$ ，这是为了减少计算时间复杂度
  • $h(0)=1$，本值的加权为1
  • $H(0)=1$，即直流增益为1，这要求 $h(t)$ 的积分为1
  • 尽可能靠近理想低通滤波器

既然有这些简单但不够准确的卷积核，那么就应该有相应的方法来判断这些卷积核的内插效果。内插效果可以通过观察这些卷积核的频谱来进行分析。

邻近

\[h(t)=\left\{\begin{split} &1\quad&|t|\le\frac12\\ &0&|t|>\frac12 \end{split}\right.\]

邻近的卷积核的时域和频域：

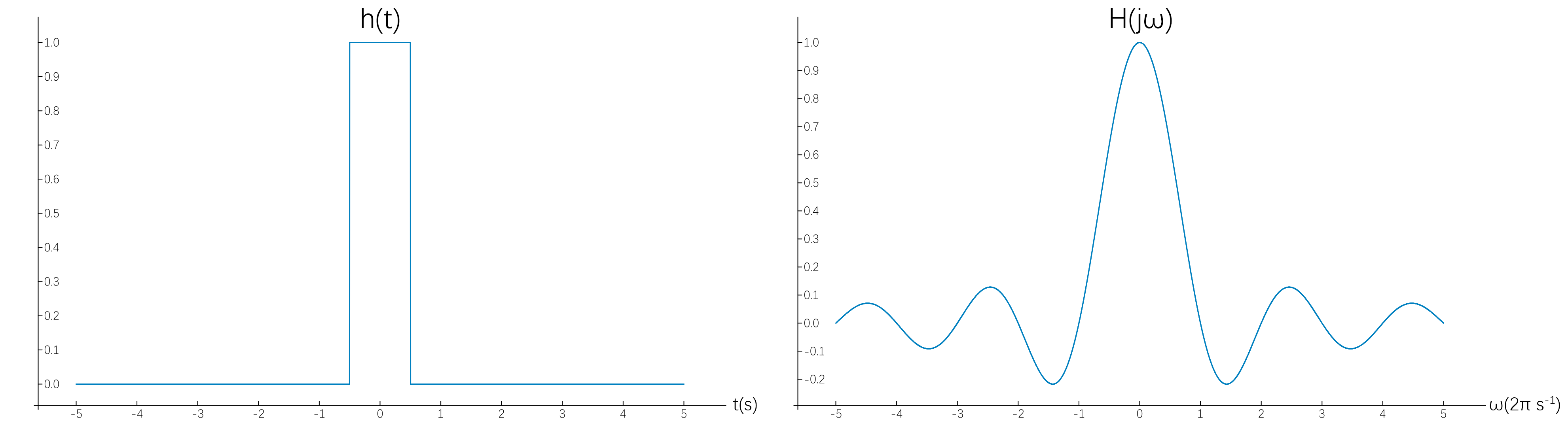
观察频域可见，邻近插值在低频保留很多，但高频溢出较多，可能不会取得令人满意的效果。

这个卷积核的效果是，插值取时间上最靠近的数据的值:

线性

\[h(t)=\left\{\begin{split} &1-|t|\quad&|t|\le1\\ &0&|t|>1 \end{split}\right.\]

线性的卷积核的时域和频域：

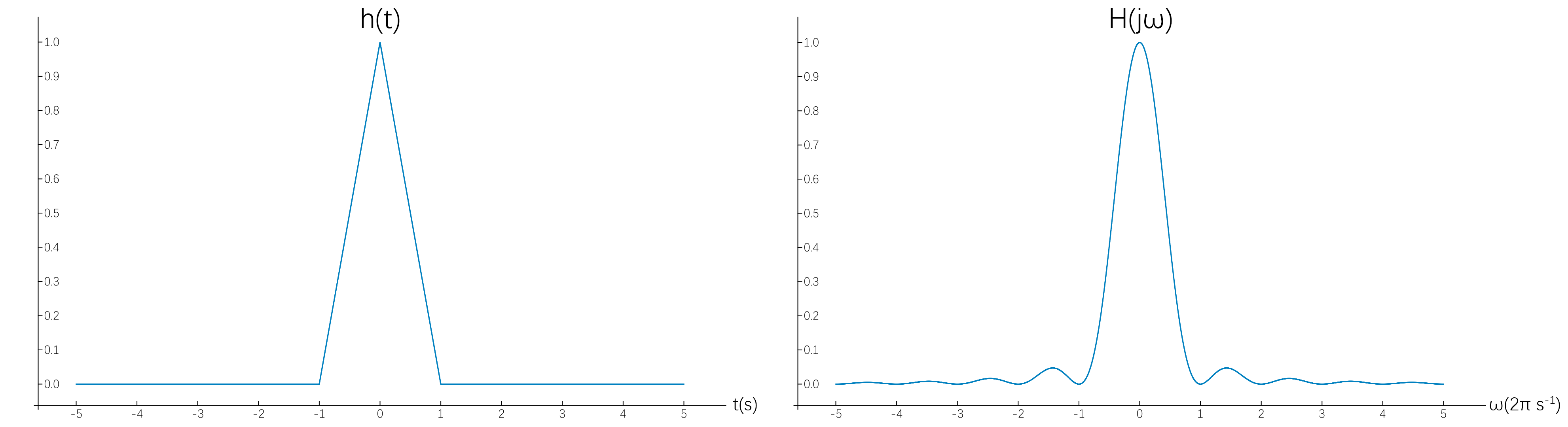
观察频域，线性插值在低频通带略窄，优点在高频溢出较少，效果比邻近插值要好不少。

这个卷积核的效果顾名思义，插值取相邻两个数据的线性插值:

三次

\[h(t)=\left\{\begin{split} &(a+2)|t|^3-(a+3)|t|^2+1\quad&|t|\le1\\ &a|t|^3-5a|t|^2+8a|t|-4a&1<|t|\le2\\ &0&|t|>2 \end{split}\right.\]

其中 a=-0.5。三次的卷积核的时域和频域：

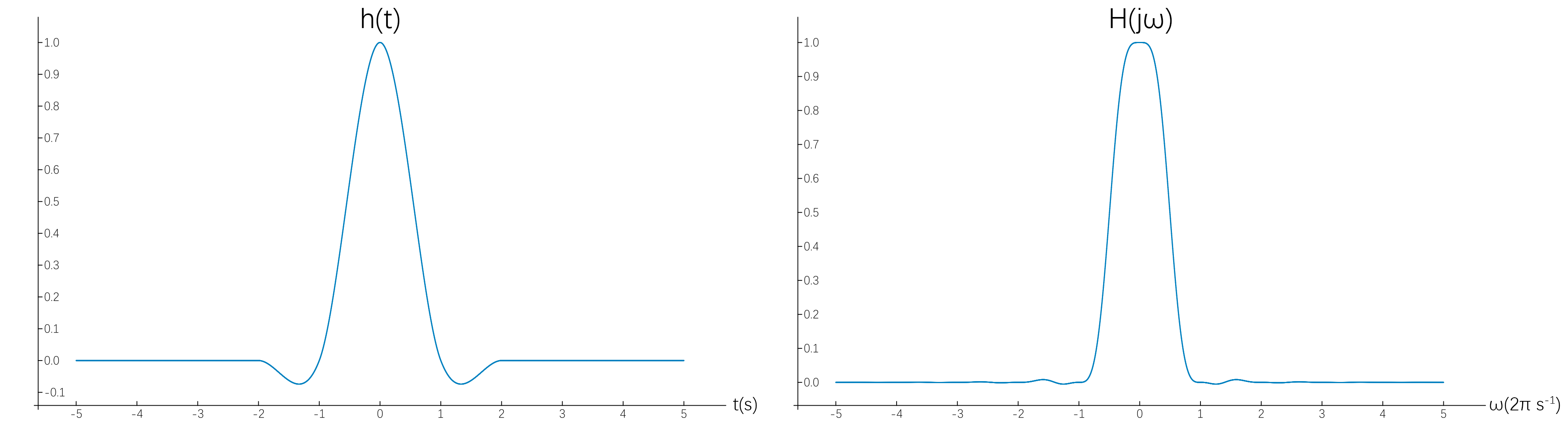
三次插值已经在一定程度上类似 sinc 函数了，它的频域性质很优秀，低频通带很宽，高频增益几乎可以忽略，效果更好。

三次卷积核的插值效果综合考虑周围四个数据点的值，可以插值得到光滑曲线:

Lanczos

\[h(t)=\left\{\begin{split} &\mathrm{sinc}(t)\mathrm{sinc}(\frac ta)\quad&|t|\le a\\ &0&|t|>a \end{split}\right.\]

其中 a=3。Lanczos卷积核的时域和频域：

Lanczos插值事实上就是 sinc 函数的有限非0区间的变体，它的频域性质最为优秀，频域几乎就是理想低通滤波，效果应该最好，但是因为含有三角函数计算，耗时也最长。

Lanczos卷积核的插值效果综合考虑周围六个数据点的值，可以插值得到光滑曲线:

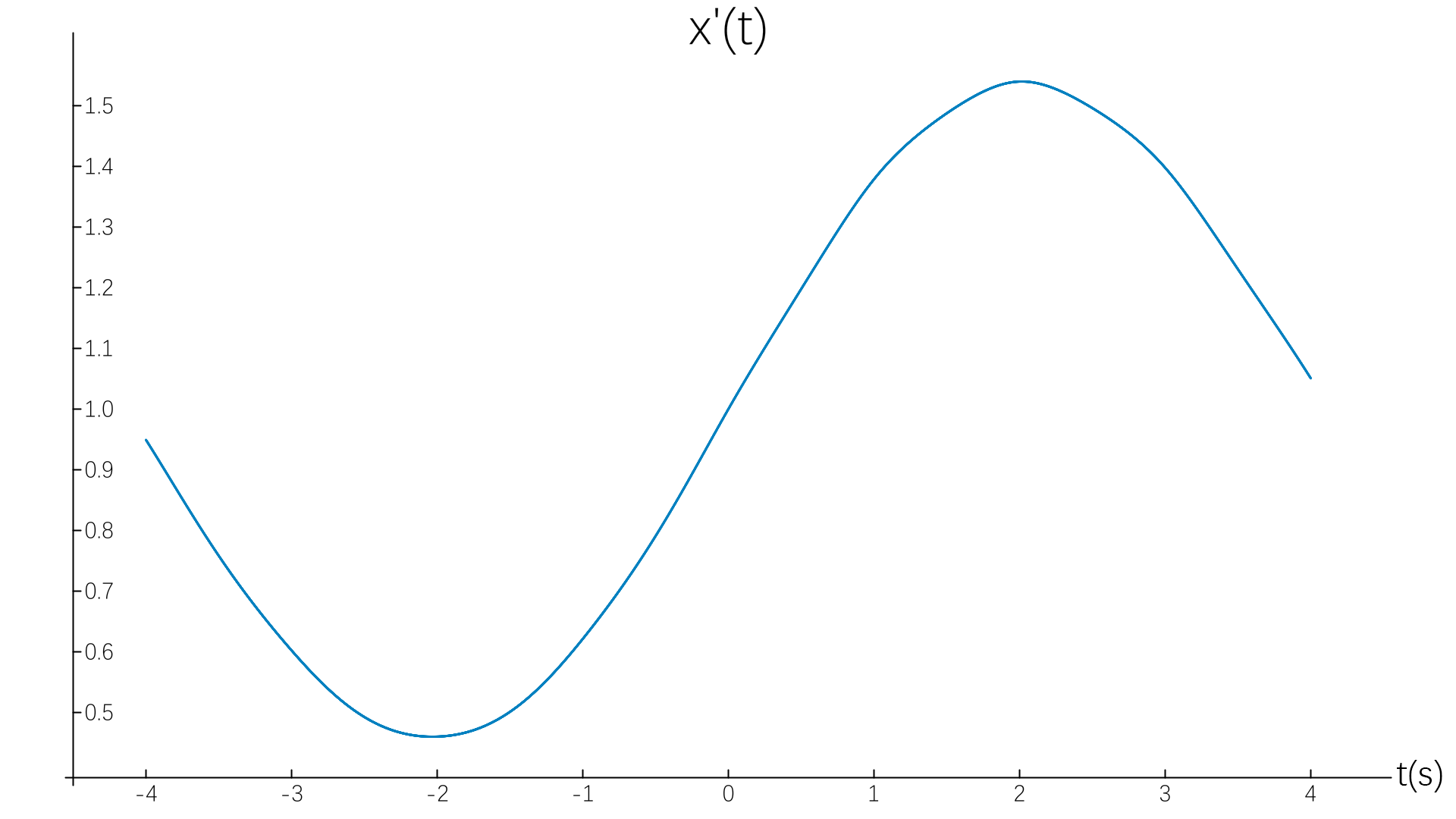
在进行下采样时，由对理想下采样滤波器的推导（见 下采样）我们知道，标准的下采样卷积核为

\[h_k(t)=k\cdot h(t)*h(kt)\]

可是这是非常难以计算的，尤其对于分段函数，而且这些特殊卷积核没有 sinc 函数的任意放缩之后离散积分也为1的性质，即

\[\sum_{n=-\infty}^{+\infty}k\cdot\mathrm{sinc}\ kn = 1\]

所以我们仿照 sinc 函数的标准下采样卷积核，选择将这些简单卷积核放慢并压低k倍来作为下采样卷积核，这里的k需要取整数。

\[h_k(t)=\frac{h(\frac t{\mathrm{round}(\frac1k)})}{\mathrm{round}(\frac1k)}\]

图片重采样

图片在本质上就是四个二维的离散信号的叠加（r, g, b, a），所以我们之前讨论的对离散时间信号的重采样一样可以用在图片的重采样上，在两个方向上分别做重采样即可。

图片重采样中比较有意思的点在于图像边缘的拓展。这是因为所有的重采样方法都需要采样点周围一个区域内的数据，如果采样点位于图像边缘，那么就需要数据的拓展。常见的拓展方法主要有补0法、循环法、和最近取值法。

  • 补零法就是把边缘之外的数据通通作为0来处理，这种方法在信号处理中是可以的，但在图像处理中效果不佳，容易出现黑边的情况。
  • 循环法将图片之外的平面看作是当前图片不断重复形成的，所以图像左边缘外的数据是右边缘内的数据，上边缘外的数据是下边缘内的数据。
  • 最近取值法意思是图像之外的一点的数据等于离它最近的有效数据点的数据，其实就是图像的边缘一圈的颜色直接向外拓展。

我采用的是最近取值法。下面给出四种重采样方法的代码。我采用模块化的方案，用一个采样框架配合不同的卷积核。代码位于 Image 类中。

//方法枚举体
enum resampling {NEAREST, BILINEAR, BICUBIC, LANCZOS};

//卷积核定义
typedef struct
{
     function&lt;double(double)&gt; h;    //卷积核函数
     double boundary;               //非0界
}Kernel;

//邻近
const Kernel nearest = {
    .h = [](double x)->double{return 1;},
    .boundary = 0.5,
};

//双线性
const Kernel biLinear = {
    .h = [](double x)->double{return 1 - abs(x);},
    .boundary = 1,
};

//双三次
const Kernel biCubic = {
    .h = [](double x)->double{
        x = abs(x);
        return (x < 1) ? (1.5 * x * x * x - 2.5 * x * x + 1) :
                        (-0.5 * x * x * x + 2.5 * x * x - 4 * x + 2);
    },
    .boundary = 2,
};

//lanczos
const Kernel lanczos = {
    .h = [](double x)->double{return x == 0 ? 1 : (3 * sin(PI * x) * sin(PI * x / 3)) / (PI * PI * x * x);},
    .boundary = 3,
};

//重采样函数，参数(x坐标，y坐标，重采样比率（小于1为缩小，大于1为放大），重采样类型（枚举中选择）)
Color resample(double x, double y, double kx, double ky, resampling type)
{
    double r = 0, g = 0, b = 0, a = 0, h;
    int u, v;
    Color pc;

    //整数化 k
    if (kx > 1) kx = 1;
    kx = 1 / round(1 / kx);
    if (ky > 1) ky = 1;
    ky = 1 / round(1 / ky);

    //找到所用的卷积核
    const Kernel* kernel;
    switch (type)
    {
        case NEAREST: kernel = &nearest; break;
        case BILINEAR: kernel = &biLinear; break;
        case BICUBIC: kernel = &biCubic; break;
        case LANCZOS: kernel = &lanczos; break;
    }

    //遍历卷积核的非0区域
    for (int i = ceil(x - kernel->boundary / kx); i <= floor(x + kernel->boundary / kx); i++)
        for (int j = ceil(y - kernel->boundary / ky); j <= floor(y + kernel->boundary / ky); j++)
        {
            //最近取值法扩展取色
            if (i < 0) u = 0;
            else if (i >= width) u = width - 1;
            else u = i;
            if (j < 0) v = 0;
            else if (j >= height) v = height - 1;
            else v = j;
            pc = getPixel(u, v);

            //按公式进行重采样计算（颜色按透明度加权）
            h = kx * ky * kernel->h(kx * (i - x)) * kernel->h(ky * (j - y));
            r += pc.alpha * pc.red * h;
            g += pc.alpha * pc.green * h;
            b += pc.alpha * pc.blue * h;
            a += pc.alpha * h;
        }
    r /= a;
    g /= a;
    b /= a;

    //返回钳位过的颜色
    return {
        (uint8_t)clamp(r, 0, 255),
        (uint8_t)clamp(g, 0, 255),
        (uint8_t)clamp(b, 0, 255),
        clamp(a, 0, 1)
    };
}

这样我们就可以实现我们的缩放函数了：

//按宽高缩放图片（可变形）
Image resize(int width, int height, resampling type)
{
    double kx = (double) this->width / width;
    double ky = (double) this->height / height;
    Image res(width, height);
    for (int i = 0; i < width; i++)
        for (int j = 0; j < height; j++)
            res.setPixel(i, j, resample(kx * i, ky * j, 1 / kx, 1 / ky, type));
    return res;
}

//只按高度缩放图片（不变形）
Image resize(int height, resampling type)
{
    int width = this->width * height / this->height;
    return resize(width, height, type);
}

效果展示

放大

一般图片的放大

对于下面的彩色小图，分别用四种方法对其放大

邻近重采样，放大，320×200，用时: 0.158s
双线性重采样，放大，320×200，用时: 0.253s
双三次重采样，放大，320×200，用时: 0.496s
Lanczos重采样，放大，320×200，用时: 1.202s

效果是非常明显的，邻近重采样就是马赛克的放大版，而剩下三个都拥有平滑的能力。剩下三个中双线性重采样效果最差，图像较模糊且有方格样的花纹。双三次重采样与Lanczos重采样效果相近，仔细区分还是能看出差距：后者的结果较前者更加清晰和锐利。

双色图片的放大

对于下面的黑白小图，分别用四种方法对其放大

邻近重采样，放大，215×200，用时: 0.211s
双线性重采样，放大，215×200，用时: 0.223s
双三次重采样，放大，215×200，用时: 0.472s
Lanczos重采样，放大，215×200，用时: 0.945s

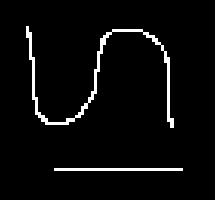
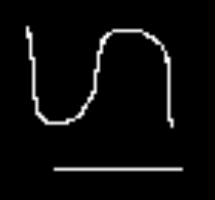
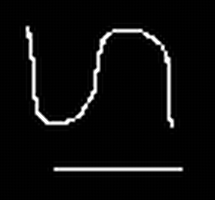
缩小

一般图片的缩小

对于下面的彩色大图，分别用四种方法对其缩小

邻近重采样，缩小，355×200，用时: 0.566s
双线性重采样，缩小，355×200，用时: 1.139s
双三次重采样，缩小，355×200，用时: 2.319s
Lanczos重采样，缩小，355×200，用时: 10.866s

结果与放大是一致的，效果依次变好。邻近重采样有很多毛刺，效果最差。剩下三个方法，结果都很平滑，但是双线性重采样图像较为模糊。双三次重采样与Lanczos重采样效果非常相近，但后者的结果较前者边缘更加清晰（注意眼睛部分）。

双色图片的缩小

对于下面的黑白大图，分别用四种方法对其缩小

邻近重采样，缩小，355×200，用时: 0.202s
双线性重采样，缩小，355×200，用时: 0.356s
双三次重采样，缩小，355×200，用时: 1.137s
Lanczos重采样，缩小，355×200，用时: 6.087s

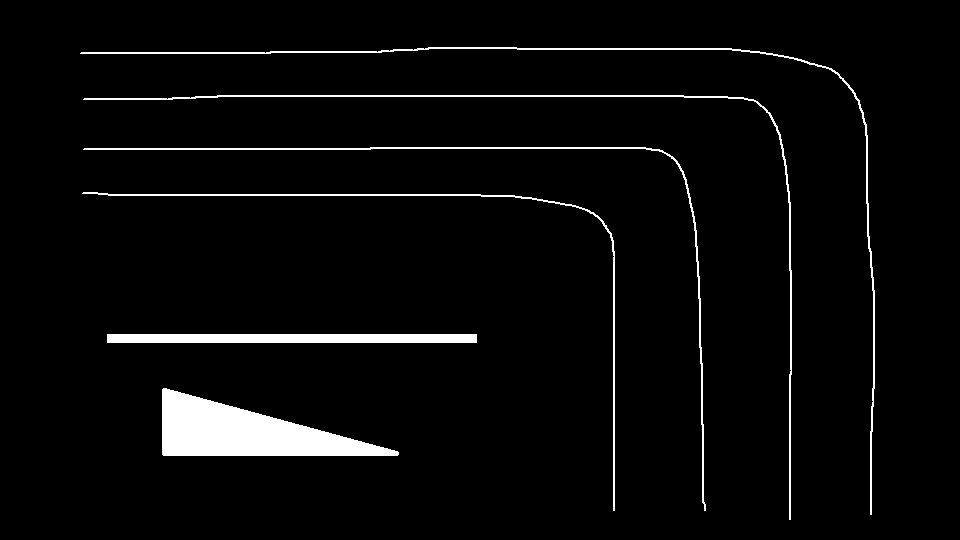
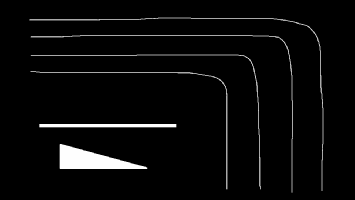
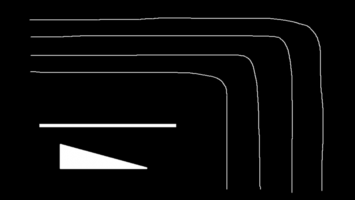
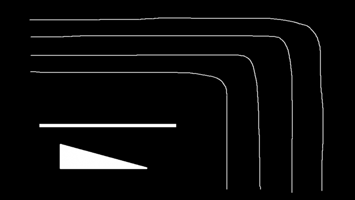
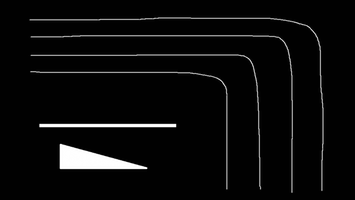
这些效果上的差距，都能在频域上找到答案：

  • 邻近重采样有很多毛刺或者马赛克样，这是因为它的频域上高频溢出严重，高频分量会造成混叠，导致采样容易出现极端不平滑值。
  • 双线性重采样图像模糊，这是因为从频域上看，它的通带太窄，保留的频率太低，就会模糊
  • 双三次重采样与Lanczos重采样效果相近，但总体后者更清晰，这从二者的频域上就能看出端倪：两者都是较好的低通滤波器，但后者相比前者更接近理想状态，通带更宽。

代码

本节代码请查看：🔗Github: JeffreyXiang/DrawWithCpp

总结

在本篇博文中，我主要讲解了离散时间信号的重采样技术，并将其拓展到二维离散信号以用于图像的缩放与变形计算。然后实现了它们的算法并成功的进行了图片的缩放。

预告

下篇文章我将讲解点阵字库的结构与图片中插入文字的实现。